Условия равновесия при фазовом переходе. Правило фаз Гиббса

Гомогенные и гетерогенные термодинамические системы

ЛЕКЦИЯ 10

Гомогенной называют такую систему, химический состав и физические свойства которой во всех ее частях одинаковы или изменяются непрерывно (без скачка) от одной точки системы к другой, а также между любыми частями которой нет поверхности раздела. Примером гомогенной системы может служить смесь газов, жидкий и твердый раствор, а также любое химически однородное тело.

Гетерогенной называют систему, состоящую из двух и более гомогенных областей или состоящей из отдельных областей, разграниченных поверхностями раздела.

Гомогенные области в гетерогенной системе наз. фазами. Каждая фаза отделена от соседней поверхностью раздела, при переходе через которую скачкообразно изменяются хим. состав или физ. свойства вещества. Примером гетерогенной системы может служить вода с плавающим в ней льдом.

Гомогенная система и каждая фаза гетерогенной системы, могут состоять из одного или нескольких чистых веществ.

Гомогенную систему или фазу гетерогенной системы, состоящую из нескольких чистых веществ, наз. раствором или смесью.

Все чистые вещества и растворы могут находиться в трех агрегатных состояниях: газообразном, жидком и твердом.

Состояние равновесия – это такое состояние, к которому при данных внешних условиях стремится термодинамическая система.

Состояние устойчивого равновесия (стабильное состояние) характерно тем, что если каким-либо внешним воздействием вывести из него рассматриваемую систему, а затем снять это внешнее воздействие, то система сама возвратится в исходное состояние равновесия.

Если систему, находящуюся в состоянии неустойчивого равновесия (лабильное равновесие) из него вывести, то она уже не возвратится в исходное состояние, я перейдет в состояние устойчивого равновесия. Даже очень малые внешние воздействия выводят систему из лабильного состояния.

Состояние относительно устойчивого равновесия (метастабильное состояние) – это состояние, в котором система может находится в течение длительного времени, причем слабые внешние возмущения, вызывающие отклонения системы от метастабильного состояния, не приводят к переходу в другое состояние; после того, как такое внешнее воздействие снято, система возвратится в исходное метастабильное состояние.

Рассмотрим изолированную систему, состоящую из двух или более фаз. Установим для такой системы общие условия фазового равновесия.

Предположим, что система состоит из двух подсистем 1 и 2, например, сосуд постоянного объема V с идеально теплоизолированными стенками, учтем, что вещество в подсистемах находится в двух разных фазах, например, в нижней части сосуда находится вода, а верхней – водяной пар. Причем количество вещества в подсистемах может меняться вследствие перехода из одной фазы в другую.

Такую систему, учитывая, что V_сис=const, m=const, U=const, можно представить себе, записав для нее следующие выражения:

V=V₁+V₂; (10.1) m=m₁+m₂; (10.2) U=U₁+U₂, (10.3)

где индексы 1 и 2 относятся соответственно к 1-ой и 2-ой фазам. Т.к. система изолирована, то получается: dV₁= - dV₂; (10.4)

dm₁= - dm₂, (10.5) dU₁= - dU₂, (10.6)

При состоянии термодинамического равновесия энтропия изолированной системы сохраняет постоянное (максимальное значение), т.е. в состоянии равновесия: dS=0, (10.7)

Поскольку энтропия явл. аддитивной величиной, применительно к рассматриваемому случаю: S=S₁+S₂, (10.8).

И, следовательно: dS=dS₁+dS₂=0, (10.9)

Найдем выражение для полного дифференциала энтропии подсистемы 1. В рассмат- риваемой подсистеме S₁ явл. функцией не только V₁ и U_1, но и m₁, т.е.: S₁=f (V₁, U₁, m₁).

В соответствие с этим:

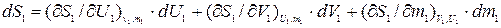, (10.10)

Как известно: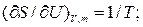

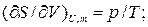
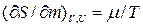
Где 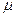- химический потенциал или изобарно-изотермический потенциал (он позволяет рассчитать изменение характеристической функции любой системы при изменении количества вещества в системе):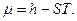

С учетом этих соотношений выражение (10.10) приобретает следующий вид:

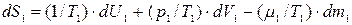(10.11)

Аналогично находим полный дифференциал энтропии подсистемы 2:

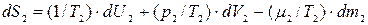, (10.12)

Из выражений (10.9), (10.11) и (10.12) с учетом соотношений (10.4) – (10.6) имеем:

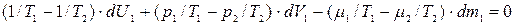, (10.13)

Поскольку дифференциал dV₁, dU₁, dm₁ взаимно независимы, то для выполнения (10.13) необходимо, чтобы были равны нулю сомножители при дифференциалах dV₁, dU₁, dm₁, т.е. чтобы:

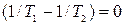, (10.14) 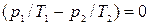, (10.15) 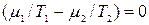, (10.16)

Откуда получаем следующие условия: T₁=T₂, (10.17); р₁=р₂, (10.18); 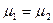, (10.19)

Таким образом, если две фазы находятся в равновесии, то температуры, давления и химические потенциалы этих фаз равны между собой. Равенство химических потенциалов фаз означает, что в условиях равновесия удельные энергии в фазах равны.

Из условий равновесия (10.17) – (10.19) следует, что если в системе, состоящей из нескольких фаз, будет наблюдаться равновесное состояние, то они не дают возможности заключить, сколько фаз могут находиться между собой в равновесии. Ответ на этот вопрос дает правило фаз Гиббса. Правило фаз, установленное Гиббсом, определяет зависимость между числом независимых параметров системы в состоянии равновесия, числом фаз и числом компонентов системы. Это правило записывается в виде: N = n – φ + 2, (10.20)

где N – число независимых параметров (переменных) системы, n – число компонентов системы, 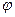- число фаз в системе.

Величина N наз. также числом термодинамических степеней свободы системы. Она показывает, какое число параметров системы, находящейся в состоянии равновесия, можно изменить произвольно, не изменяя при этом числа фаз в системе. Очевидно, величина N всегда положительна, причем она может быть равной нулю, т.е. N 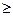0. Для однокомпонентной системы, состоящей из одной фазы, находим N=2. Это означает, что состояние простых однородных систем (идеальный газ, однородная жидкость) определяется двумя независимыми параметрами. Для многокомпонентных систем число степеней свободы может быть больше двух, и для определения состояния, кроме двух термодинамических параметров необходимо знать концентрации компонентов. Из уравнения (10.20) видно, что с увеличением числа фаз в системе, N – уменьшается, т.е. число свободно варьируемых параметров убывает. Правило фаз выполняется для всех возможных систем, не смотря на проходящие в них фазовые превращения и химические реакции, оно справедливо для веществ в любых агрегатных состояниях.

В условиях равновесия термодинамической системы правило фаз Гиббса записывается в виде: 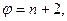(10.21)

Дата добавления: 2014-11-29