Реальные циклы ГТУ

Реальные циклы ГТУ отличаются от идеальных тем, что в действительных циклах учитываются неизбежные тепловые потери.

На рис. 25.5 показан реальный цикл ГТУ, протекающий с потерями.

Сжатие воздуха происходит не по изоэнтропе 1-2, как это было при рассмотрении идеального цикла, а с потерями тепла, по некоторой политропе 1-2¢. Потери

компрессоре обычно оценивают адиабатным К.П.Д., который приближенно определяют по

формуле, полагая что c_p = const

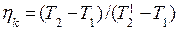, (25.13)

откуда: T₂¢ – T₁ = (T₂ – T₁)/h_k, (25.14)

Линия 2¢-3 отображает изобарный процесс подвода тепла в цикл. Давление в точке 2¢ несколько выше давления перед газовой турбиной в точке 3 вследствие гидравлических потерь в камере сгорания и коммуникациях.

Расширение рабочего тела в газовой турбине совершается с потерями и сообразно с этим отображается некоторой политропой 3-4¢. Потери тепла в газовой турбине характеризуются относительным внутренним К.П.Д., который в предположении, что c_p = const, определяют по формуле:

h_oi = (T₃ – T₄¢)/(T₃ – T₄), (25.15)

откуда: T₃ – T₄¢=h_oi (T₃ – T₄), (25.16)

Тепло отводится из цикла в изобарном процессе,отображаемом линией 4¢-1.

Термический К.П.Д. ГТУ будет равен

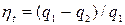, (25.17)

где q₁ = c_p (T₃ – T₂¢); q₂ = c_p (T₄¢ – T₁)

Полезная работа:

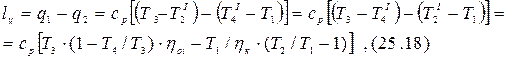
Поскольку линия 1-2 отображает изоэнтропный процесс

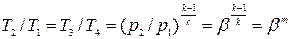, (25.19)

где m = (k-1)/k

После подстановки в формулу (25.18), служащую для определения полезной работы, значений из формулы (25.19), получим:

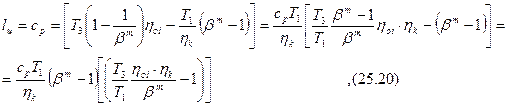
Для ГТУ величины c_p, T₁, h_k и h_oi можно считать постоянными и в связи с этим полагать, что величина работы l_ц является функцией величин Т₃ и b^m, т.е. l_ц = f(T₃,b^m). Сообразно с этим для каждого значения Т₃, которому отвечает вполне определенная степень повышения давления воздуха в компрессоре, можно построить кривую зависимости l = f(b^m).

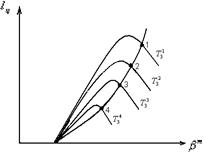
Рассмотрим характер такой кривой для произвольно выбранного значения Т₃. Заметим, что уравнение этой кривой в двух случаях обращается в ноль, а именно: при b^m = 1 и при b^m = . Из этого можно заключить, что в интервале между этими значениями l_ц имеется максимальное значение величины l_ц и, следовательно, кривая l_ц = f(b^m) имеет примерно вид, показанный на рис. 25.4 Линия 1-2-3-4 представляет собой кривую максимальных значений l_цдля различных значений Т₃. Найдём выражение, служащее для определения максимального значения l_ц, отвечающего заданной температуре Т₃.

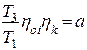Положим, что b^m = x и , тогда выражение (25.20) примет вид: 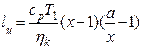, (25.21)

Для определения максимума этой функции приравняем к нулю её производную, отбросив при этом постоянную величину c_pT₁/h_k и после преобразований

Рис. 25.4

получим:

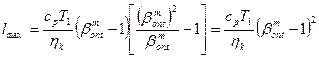, (25.22)

и поэтому h_t = l_max/q₁ (25.23)

25.4. Цикл ГТУ с подводом теплоты при p = const
и регенерацией

В ГТУ основными являются потери теплоты с уходящими из турбины газами. На рис. 25.5 изображена принципиальная схема (тепловая) ГТУ, в которой теплоту уходящих газов частично используют для нагревания сжатого воздуха. Такой цикл называют регенеративным.

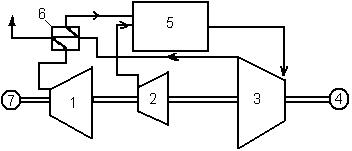1 – воздушный компрессор;

2 – топливный компрессор (насос); 3 – газовая турбина;

4 – электрический генератор;

5 – камера сгорания;

6 – регенератор;

7 – пусковой электродвигатель.

Как видно из рис. 25.7,

Рис.25.5 уходящие газы после газовой турбины 3 направляются в регенератор 6, где они подогревают сжатый воздух (от температуры Т₂ до Т₅), в результате чего уходящие газы охлаждаются (от Т₄ до Т₆) и вследствие этого К.П.Д. установки повышается. Величина повышения К.П.Д. зависит от изменения температуры воздуха и газов или так наз. степени регенерации.

Термодинамический цикл ГТУ со сгоранием топлива при p = const и с регенерацией теплоты состоит из следующих процессов (идеальный цикл): 1-2 – процесс сжатия воздуха в компрессоре, который может быть как изотермический, так и адиабатным; 2-5 – изобарный подогрев воздуха в регенераторе: 5-3 – изобарный процесс подвода теплоты в камере сгорания за счет сгорания топлива; 3-4 – адиабатное расширение газов в турбине; 4-6 – изобарное охлаждение рабочего тела в регенераторе; 6-1 – изобарная отдача рабочим телом теплоты окружающему воздуху (рис. 25.6).

На T-S-диаграмме теплота, отдаваемая продуктами сгорания на участке изобары 4-6 (пл. с-6-4-d-c), подводится в регенераторе и сжатому воздуху на участке изобары 2-5.

Регенерация будет полной, если охлаждение продуктов сгорания в регенераторе

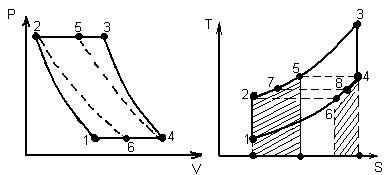происходит до температуры воздуха, поступающего в него, т.е. от Т₅ = Т₄ до Т₆ = Т₂. При этом количество теплоты, воспринятое воздухом регенератора, равно количеству теплоты, отдаваемому в нём продуктами сгорания:

с_р(Т₅ – Т₂) = с_р(Т₄ – Т₆) (25.24)

Рис. 25.6

При c_p = const имеем

Т₅ – Т₂ = Т₄ – Т₆, (25.25)

Количество подведенной теплоты в цикле с полной регенерацией:

q₁ = c_p(Т₃ – Т₅) = с_р(Т₃ – Т₄), (25.26)

Количество отводимой теплоты в цикле с полной регенерацией:

q₂ = c_p(Т₆ – Т₁) = с_р(Т₂ – Т₁), (25.27)

Тогда:

, (25.28)

Согласно (25.6) – (25.8): ; ;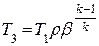

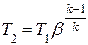
Термический К.П.Д. с полной регенерацией:

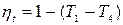, (25.29)

Из этого выражения видно, что h_{т ГТУ} при p = const с полной регенерацией теплоты и адиабатным сжатием воздуха в компрессоре зависит от температуры газа в конце адиабатного расширения Т₄ и начальной температуры газа Т₁.

Однако полная регенерация теплоты практически невозможна вследствие ограниченных размеров регенераторов и наличия конечной разности температур между нагреваемым и охлаждаемым потоками газа. Обычно нагреваемый в регенераторе воздух имеет температуру Т₇, несколько меньшую, чем Т₅, а охлаждаемые газы – температуру Т₈, более высокую, чем Т₆.

Полнота регенерации теплоты определяется степенью регенерации, т.е. отношением теплоты, которое фактически используется в процессе регенерации (процесс 2-5), к располагаемой теплоте, соответствующей возможному перепаду температур от Т₅ до Т₂.

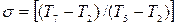, (25.30)

Определим h_т цикла с неполной регенерацией. Величина степени регенерации зависит от конструкции теплообменника или от величины рабочих поверхностей теплообменника (регенератора). Чем больше s, тем полнее в цикле осуществляется регенерация и тем в большей степени используется теплота отработанных газов. При s = 0 установка работает без регенерации, при полной регенерации Т₇ = Т₅ и s = 1. Значение s изменяется в пределах от 0,5 до 0,7.

Определим h_т цикла с неполной регенерацией.

Количество подведенной теплоты q₁ в цикле с неполной регенерацией опр. так: q₁ = c_p(T₃ – T₇) = c_p(T₃ – T₂) – c_p(T₇ – T₂), (25.31)

или q₁ = c_p[(T₃ – T₂) – s(T₅ – T₂)], (25.32)

Количество отведенной теплоты q₂ в этом цикле на q₇₂ = c_p(T₇-T₂) меньше, чем в цикле без регенерации, т.е.

q₂ = c_p(T₄ – T₁) – c_p(T₇ – T₂) = c_p[(T₄ – T₁) – s(T₅ – T₂)], (25.33)

Тогда 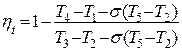, (25.34)

Выразив температуры Т₂, Т₃, Т₄, Т₅, через Т₁ и параметры цикла, получим:

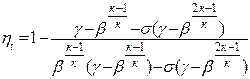, (25.35)

где g = Т₅/Т₂

25.5. Цикл ГТУ при p = const с изотермическим сжатием
воздуха в компрессоре

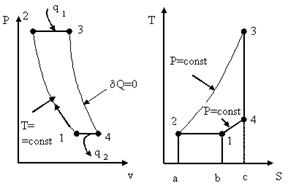В этом случае теплота от рабочего тела к холодильнику будет отводиться и в изобарном процессе 4-1 (пл. в-1-4-с) и в изотермическом процессе сжатия 1-2 (пл. а-2-1-в); при этом количество теплоты, отводимой в изобарном процессе 4-1, составляет:

q₂¢ = c_p(T₄ – T₁), (25.36)

а количество теплоты, отводимой в изотермическом процессе 1-2, будет:

Рис. 25.7

q₂¢¢ = RT₁ln(p₂ /p₁), (25.37)

таким образом, в сумме:

q₂=q₂¢+q₂¢¢=c_p(T₄–T₁)+RT₁ln(p₂/p₁), (25.38)

Количество теплоты, подводимой к рабочему телу в изобарном процессе 2-3:

q₁ = c_p(T₃ – T₂), (25.39)

Подставляя эти значения q₁ и q₂ в общее соотношение для h_т, получим:

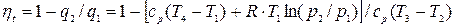, (25.40)

Разделив числитель и знаменатель правой части этого уравнения на с_рТ₁ и учтя, что Т₁ = Т₂ и что для идеального газа: 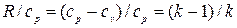, получим:

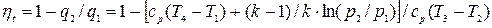, (25.41)

Учитывая, что: 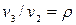, а при p = const (процесс 2-3)

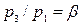, а в адиабатном процессе 3-4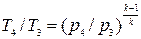

или что то же самое (поскольку р₃ = р₂ и р₁ = р₄)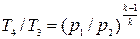

Подставляя их значения в уравнение (25.41) и учитывая, что 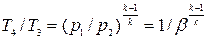, получим

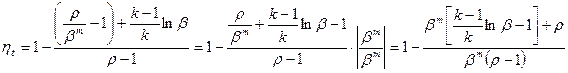,(25.42)

Дата добавления: 2014-11-29