Химическое равновесие в неидеальных системах

Закон действующих масс (V, 5) применим, как уже говорилось, лишь к идеальным газам (или идеальным растворам). Для таких систем произведение равновесных относительных парциальных давлений реагирующих веществ, равное K ⁰, не зависит от общего давления. Применение этого закона к реальным системам неизбежно носит приближенный характер, при этом неточность закона должна возрастать с увеличением давления и понижением температуры.

Ниже дан пример зависимости «константы» равновесия реакции N ₂ + 3 H ₂«2 NH ₃ от давления (при t = 450°C):

Р, атм.
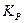
	6,55×10^-3	6,71×10^-3	6,85×10^-3	7,20×10^-3	8,77×10^-3	12,8×10^-3	22,8×10^-3

Из приведенных данных следует, что при изменении давления в системе от 10 до 1000 атм. «константа» изменяется почти в четыре раза, что связано с отклонением поведения реальных газов от идеальности.

Свойства реального газа существенно зависят от межмолекулярных взаимодействий. В обычных условиях, когда средняя потенциальная энергия взаимодействия молекул намного меньше их средней кинетической энергии, свойства реального газа незначительно отличаются от свойств идеального газа. Отличие свойств реального газа от свойств идеального газа становится особенно значительным при высоких давлениях и низких температурах.

Принципиально возможны два способа изучения равновесия в реальных системах.

Первый основан на использовании вместо закона идеального газа уравнения состояния реального газа (например, уравнения Ван-дер-Ваальса или какого-либо другого). А именно, в дифференциал dG = VdP можно подставить V или dP, определенные из выбранного уравнения состояния, и далее вывести закон равновесия, заменяющий закон действующих масс. Этот путь использовался и оказался неудачным. Во-первых, любое уравнение состояния является приближенным и бóльшая точность связана с бóльшей сложностью уравнения. Во-вторых, само выражение закона зависело бы от выбранного в достаточной степени произвольно уравнения состояния. Таким образом, было бы неизбежно появление различных законов равновесия в зависимости от вкуса и требований автора, не говоря уже о математических сложностях, связанных с их выводом.

Иной путь решения задачи предложил Гилберт Льюис, который ввел в термодинамику понятия фугитивности (летучести) f и активности a.

Фугитивность — величина, не имеющая определенного физического смысла, но будучи подставленной в термодинамические уравнения, выведенные для идеального газа, она делает их пригодными для реального газа. По этой причине фугитивность иногда называют исправленным давлением.

Хотя этот прием является формально-математическим, однако он, бесспорно, оказался удобным и продуктивным.

Таким образом, фугитивность (летучесть) — термодинамическая величина, которая служит для записи зависимости химического потенциала индивидуальных веществ или компонентов смеси от параметров состояния (давления, температуры и состава).

Для индивидуального (реального) газа фугитивность f (T,P) определяется соотношением:

(V, 19)

где μ (T, Р) — химический потенциал вещества, μ ⁰(T) — его стандартный химический потенциал, равный химическому потенциалу в некотором гипотетическом состоянии, в котором при данной температуре и давлении равном 1 атм., газ обладал бы свойствами идеального газа; 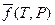— относительная фугитивность вещества; R — универсальная газовая постоянная. Кроме фугитивности чистого вещества, определяемой соотношением (V, 18), для реальных газовых смесей вместо парциального давления вводят также парциальную фугитивность. Делается это с помощью выражения (III, 52) для химического потенциала компонента в смеси (парциального мольного изобарного потенциала):

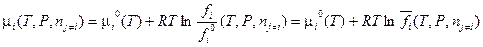(V, 20)

где — число молей компонентов смеси, кроме i -ого компонента; 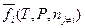— относительная парциальная фугитивность.

Из приведенного определения фугитивности следует, что она измеряется в единицах давления. Стандартное состояние в выражениях (V, 19) и (V, 20) относится к P ⁰ = ¦⁰ = 1 атм.

Так как с понижением давления поведение газа приближается к идеальному, то в пределе

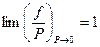
Широко применяется понятие коэффициента фугитивности (летучести), определяемого соотношением:

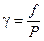(V, 21)

Коэффициент фугитивности (летучести) характеризует степень отклонения газа от идеального, это безразмерная величина. Его численное значение может быть и меньше, и больше единицы. В пределе, когда Р стремится к нулю, коэффициент γ стремится к единице:

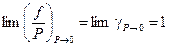
Перейдем к описанию химического равновесия в реальных системах. На основе общего условия равновесия реакции (IV, 11), т. е. , а также выражения химического потенциала в форме (V, 20), можем вывести уравнение изотермы реакции в реальной газовой смеси, по форме совпадающее с уравнением изотермы Вант‑Гоффа, т. е.

(V, 22)

где (D G_T) — изменение изобарного потенциала, соответствующее одному пробегу реакции при условии постоянства исходных значений фугитивностей , стоящих во втором слагаемом справа. В первом слагаемом значения фугитивностей 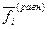соответствуют равновесному состоянию.

На основании (V, 22) также можно записать закон действующих масс для реальной системы, по форме совпадающий с (V, 5):

Если воспользоваться определением коэффициента фугитивности (летучести) (V, 21), то константу равновесия можно представить в таком виде:

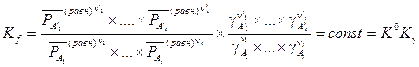(V, 23)

где вводится обозначение .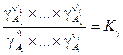

Здесь использовано прежнее обозначение K ⁰ и введено новое K _g. Важно понять, что величина K _g в реальных системах не является константой, она зависит от давления. При расчетах равновесий в реальных системах чаще всего поступают так: определяют K ⁰ для достаточно низких давлений, когда K _g» 1. Затем для заданных давления и температуры находят коэффициенты фугитивности и по соотношению (V, 23) определяют значение K ⁰ для этих условий. Далее, считая применимым закон Дальтона, вычисляют, как уже описано, равновесную степень превращения и состав равновесной смеси.

Равным образом вместо константы равновесия K _c для реальной системы следует записать

,

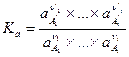где a — активность компонента, заменяющая его концентрацию в реальной смеси в выражении (III, 54), т. е.

В таком виде уравнение химического потенциала используется и для компонентов жидкого раствора.

По аналогии с коэффициентом фугитивности вводится понятие коэффициента активности, характеризующего степень отклонения раствора от идеального,

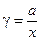
Дата добавления: 2014-11-29