Методы расчета фугитивности (летучести)

Чтобы вычислить фугитивность, необходимо знать явную зависимость её от давления при постоянной температуре.

Энергия Гиббса как функция давления и температуры определяется по уравнению (III, 31):

dG = – SdT + VdP

Тогда при T = const оно сводится к виду dG =VdP.

Интегрирование этого уравнения для одного моля вещества дает следующий результат:

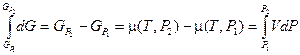
Если P ₁®0, то свойства газа приближаются к свойствам идеального газа, т. е. . Опуская индекс «2», в этом случае можем записать:

, (V, 24)

(с учетом выражения V_ид. для одного моля идеального газа из уравнения Менделеева‑Клапейрона).

Если принять во внимание, что для одного моля вещества в газообразном состоянии

(V, 25)

то подставив из (V, 19) и (III, 52) значения химического потенциала для реального и идеального газов, получим:

(V, 26)

Из сравнения уравнений (V, 24), (V, 25) и (V, 26)следует, что

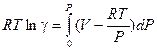
Или после простых преобразований:

(V, 27)

Разность — это так называемая объемная поправка неидеального газа, учитывающая, что объем реального газа отличается от объема идеального газа.

С учетом введенного обозначения уравнение (V, 27) можно переписать следующим образом:

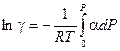(V, 28)

Полученное уравнение позволяет вычислять коэффициенты фугитивности (летучести) по экспериментальным данным. Величину интеграла находят графически по площади под кривой a = a(P) (смотри рис.22). При приближении кривой к значению Р = 0 ее приходится экстраполировать, что не представляет затруднений ввиду линейного хода кривой в области малых давлений. Представленный на рисунке график относится к водороду. Для абсолютного большинства других газов разность стремится к нулю при , а при высоких давлениях значение a может принимать отрицательные значения.

Рис. 22. К графическому определению летучести газа по зависимости объемной поправки неидеального газа от давления.

Другой графический метод расчета основан на использовании коэффициента сжимаемости. Коэффициентом сжимаемости z называется отношение 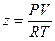. Очевидно, что для идеального газа его значение равно единице, но отличается от единицы для реальных газов.

Если принять во внимание, что

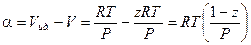
уравнение (V, 28) можно преобразовать к следующему виду:

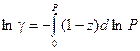
Полученный интеграл определяют графически по площади под кривой в координатах

(z – 1) – ln P.

Третий метод используют для определения коэффициента фугитивности (летучести) по изотермам идеального и реального газов в координатах P – V от достаточно низкого давления, при котором эти изотермы практически сливаются, до давления, при котором требуется определить фугитивность. Построим изотерму реального газа P = f (V) (кривая «b» на рис.23). Не представляет труда на этом же графике начертить идеальную изотерму (кривая «а» на рис.23). Выберем два давления P₂ и Р₁ и проведем соответствующие им изобары. Продифференцируем уравнение(V, 19) при условии T = const:

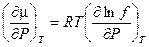
Принимая во внимание, что для одного моля газа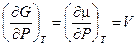
(смотри ( III, 32)), получим:

или, помня о постоянстве температуры, можем записать

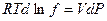
После интегрирования последнего уравнения имеем:

Из геометрических соображений (рис.23) следует, что интеграл 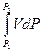будет равен площади фигуры, ограниченной реальной изотермой, двумя изобарами и осью ординат, т. е. точками 122’1’. Из рисунка также следует, что указанный интеграл можно определить как разность, полученную вычитанием из площади фигуры 133’1’, ограниченной идеальной изотермой, двумя изобарами и осью ординат площади заштрихованной области 233’2’.

Площадь фигуры, ограниченной идеальной изотермой, определяется без труда, она равна интегралу

Следовательно, , где символом «А» мы обозначили площадь заштрихованной области 233’2’.

Если теперь за Р ₁ принять такое давление, при котором реальная и идеальная изотермы совпадут, что возможно при Р ₁ ® 0, то летучесть будет равна давлению, т. е. ¦₁ = Р ₁.

В этом случае

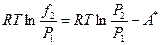или

,

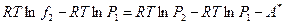где символом A ^* обозначена площадь всей фигуры, находящейся между верхней изобарой и обеими изотермами до точки их слияния.

Опуская индексы, после сокращений получим:

Следовательно, для определения летучести газа при заданном давлении Р нужно измерить площадь, заключенную между двумя изотермами от давления Р до Р = 0 или . В последнем и заключается неудобство обсуждаемого метода, т. к. трудно строить изотермы в области больших объемов и решить, где же их оборвать. Другой недостаток метода заключается в том, что вычисление площади, ограниченной двумя кривыми, связано с дополнительными погрешностями.

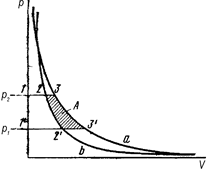
Рис. 23. Графическое определение летучести газа, где «а» — идеальная изотерма,
«b» — реальная изотерма.

Еще один метод определения фугитивности (летучести) основан на принципе соответственных состояний. Согласно этому принципу при одинаковых приведенном давлении и приведенной температуре 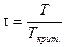значения коэффициента фугитивности (летучести) для различных веществ должны быть одинаковыми. Из понятия соответственного состояния вытекает, что коэффициент сжимаемости z, который учитывает степень отклонения неидеальных систем от идеальной, в критическом состоянии для всех веществ должен быть одинаков: .

В действительности же, его величина зависит от природы вещества. На этом основании составлены таблицы, где при определении значений коэффициентов фугитивности (летучести) учитываются не только приведенные температура и давление, но и различные значения z_крит.. Таким образом, при близости вещества к насыщенному состоянию g = g(p, t, z_крит.).

Зависимость коэффициента фугитивности (летучести) от приведенного давления при различных приведенных температурах может быть представлена на графиках, используемых для тех же определений (смотри рис. 24).

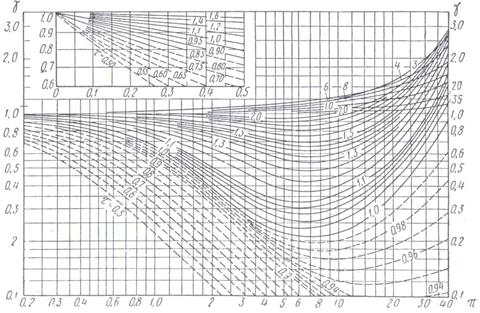
Рис. 24. Зависимость коэффициента летучести γ от приведенного давления π
и приведенной температуры τ.

Дата добавления: 2014-11-29