Задачи для самостоятельного решения. 1.1 Уравнение плоскости Преобразовать к виду в отрезках на осях

1.1 Уравнение плоскости Преобразовать к виду в отрезках на осях.

1.2 Найти уравнение плоскости, проходящей через точку Р (1,2,-1) перпендикулярно прямой

ЗАДАНИЕ №2

Для решения второй задачи потребуются следующие понятия и формулы:

Аналогично тому, как мы действовали в трехмерном случае(в пространстве) при решении первой задачи, рассмотрим на плоскости прямую. Чтобы задать прямую, нужно задать точку, через которую она проходит и вектор, задающий направление: и .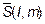

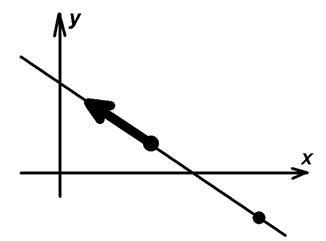
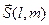
M₀ (x₀, y₀)

M(x, y)

Возьмем текущую точку прямой 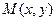и рассмотрим вектор .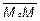

Вектор 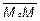коллинеарен вектору 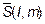и их координаты пропорциональны

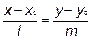- это условие и задает уравнение прямой, проходящей через заданную точку в заданном направлении.

Перенесем все в левую часть и, обозначив числовые коэффициенты другими буквами, получим общее уравнение прямой

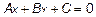
Взяв в качестве вектора 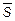вектор, соединяющий две точки прямой и ,получим уравнение прямой, проходящей через две заданные точки

.

Выразив 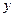и обозначив коэффициент при 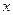буквой , а остальные слагаемые буквой , получим уравнение с угловым коэффициентом

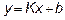
Условие параллельности двух прямых

Условие перпендикулярности двух прямых

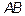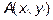Если есть отрезок , где и и точка 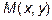делит его в заданном отношении , то есть

, то

координаты точки

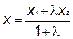; (формулы деления отрезка в заданном отношении)

Расстояние между точкам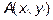и и вычисляется по формуле, полностью аналогичной формуле расстояния в пространстве, только относительно двух переменных

Пример 1. Задан отрезок 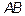, где 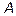(-2,5), (4,17).

Определить координаты точки 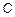, расстояние от которой до точки 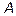в два раза больше, чем расстояние до точки .

По условию задачи

Координаты точки нам неизвестны, но она делит отрезок 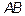в отношении .

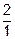Итак, =2

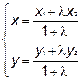
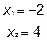
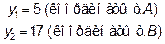
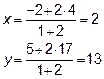
Искомая точка имеет координаты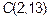

Пример 2. Прямые 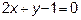и являются сторонами треугольника, а точка -точкой пересечения третьей стороны с высотой, опущенной на неё. Составить уравнение третьей стороны.

а) Точка А является точкой пересечения прямых АВ и АС, т.е. лежит и на той и на другой прямой. Значит её координаты должны удовлетворять и уравнению прямой АВ и уравнению прямой АС.

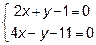сложим уравнения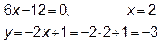

Итак, точка А (2,-3).

Высота АР – это прямая, проходящая через две заданные точки А и Р:

;

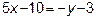
(АР)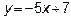

то есть угловой коэффициент 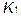высоты АР равен -5

в) Прямая ВС перпендикулярна АР, значит её угловой коэффициент

.

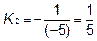Значит её уравнение с угловым коэффициентом имеет вид

(ВС) 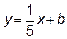, где неизвестно.

Но мы знаем, что прямая ВС проходит через точку Р, -значит координаты точки Р обращают уравнение ВС в тождество.

Подставим координаты точки Р в уравнение ВС:

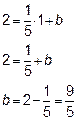
Итак, уравнение ВС:

или

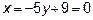
Более подробно этот материал можно найти в глава 2; §7, §8; в глава 1 §2 можно найти аналогичные решенные задачи

Выполните следующие задания:

Дата добавления: 2014-12-10