Решите самостоятельно следующую систему

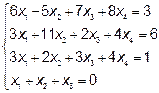
Более подробно о решении систем уравнений методом Гаусса можно почитать в [1] гл.6 §7, [2] §4. Найти подробные задачи можно в [3] гл.4 § 6 и § 7.

ЗАДАНИЕ №7

Следующие три задачи относятся только к студентам специальности ЭВМ.

Задача №7: Привести квадратичную форму 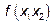к каноническому виду; найти ортонормированный базис, в котором матрица квадратичной формы имеет диагональный вид; найти матрицу перехода к ортонормированному базису.

Квадратичной формой действительных переменных 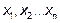называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени. Если 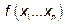- квадратичная форма переменных 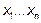, а λ – какое-то действительное число, то .

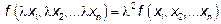Если n=2, то .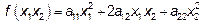

Матрица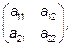

у которой 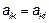, называется матрицей квадратичной формы .

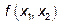Т.к. А – симметричная матрица, то корни λ₁ и λ₂ характеристического уравнения

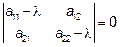
являются действительными числами.

Пусть 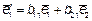и

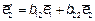
нормированные собственные векторы, соответствующие характеристическим числам λ₁ и λ₂ в ортонормированном базисе 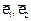. В свою очередь векторы 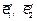образуют ортонормированный базис. Матрица

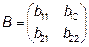
Является матрицей перехода от базиса 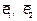к базису 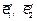. Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид:

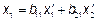
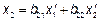
Преобразовав с помощью этих формул квадратичную форму 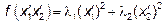, (не содержащую членов с произведениями).

говорят, что форма приведена к каноническому виду.

Пример 1. Приведем к каноническому виду квадратичную форму .

; ; .

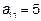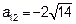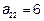Составим характеристическое уравнение

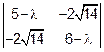=0 или .

; .

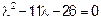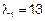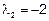Определим собственные векторы

I)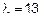

;

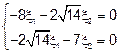
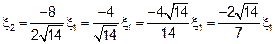Полагая что 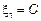, получим 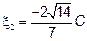, то есть собственный вектор .

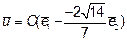II) .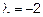

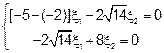
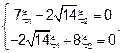
Полагая что 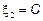, получим 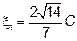, то есть собственный вектор .

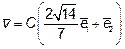Чтобы нормировать векторы u и v, следует принять .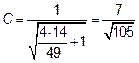

Итак, мы нашли нормированные собственные векторы

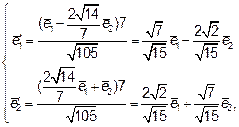
где 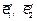- ортонормированный базис, в котором матрица квадратичной формы имеет диагональный вид.

Матрица перехода от ортонормированного базиса 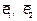к ортонормированному базису 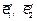имеет вид:

B=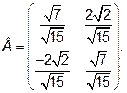

Канонический вид квадратичной формы

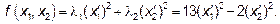
Решите эту задачу самостоятельно:

Задача 7.1. Приведите к каноническому виду квадратичную форму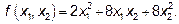

Подробнее можно об этом прочитать в [2], §23 и найти задачи на эту тему в [3] гл.5 §7.

ЗАДАНИЕ №8

Это заданиеотносится к разделу «линейные операторы»; более подробно о линейных операторах (отображениях, преобразованиях) можно прочитать в [1] гл. 6, [2] §15 и найти решённые задачи этой темы можно в [3] гл. 5 §4.

Если в линейном пространстве R каждому вектору 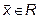по некоторому правилу поставлен в соответствие вектор 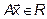, то говорят, что в пространстве R задан оператор A. Оператор A называется линейным, если для любых векторов 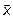и 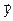и любого действительного числа λ выполняются равенства:

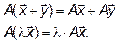
Значит, для того, чтобы проверить, является ли оператор A линейным надо проверить, выполняются ли эти равенства.

Проверим, является ли оператор A линейным в R³

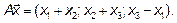
Возьмем два вектора 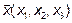и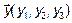

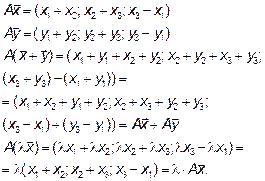
То есть оператор A является линейным, найдем его матрицу.

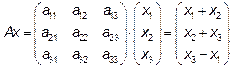
Первая координата произведения получается умножением первой строки на столбец 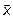, то есть 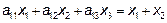, значит , ,

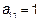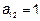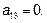
Вторая координата произведения:

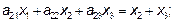
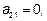
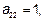
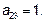
Третья координата произведения:

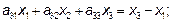
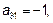
Итак, матрица оператора

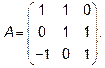
Найдем собственные значения линейного оператора:

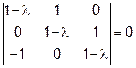
(1-λ)·(1-λ)²-1·1=0

(1-λ)³=1

1-λ=1

λ=0

Оператор A имеет собственное значение λ=0 кратности 3.

Для определения координат собственного вектора получаем систему уравнений:

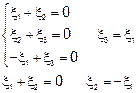
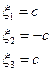
положив

получим:

Собственному числу 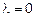соответствует собственный вектор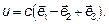

ЗАДАНИЕ №9

Чтобы решить задачу№9,необходимо уметь выполнять действия над комплексными числами в алгебраической и тригонометрической их формах. Подробно прочитать об этих числах можно в [4] гл7.

Пример 1. Выполнить действия над комплексными числами в алгебраической форме.

Решение: Алгебраической формой комплексного числа называется следующий его вид z=x+iy. Действия над комплексными числами в алгебраической форме производятся как над многочленами вида a+xb. Специфическим приёмом деления комплексного числа на комплексное число является домножение и числителя и знаменателя на комплексно сопряжённое знаменателю число. В результате частное не изменится, но делитель будет вещественным.

Заметим что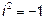

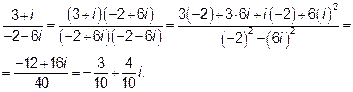
Пример 2. Найти тригонометрическую форму числа 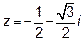. Найти: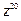

Решение: Выражение вида 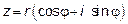называется тригонометрической формойчисла z, где модулем z называют 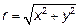, аргументом z – угол 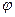между радиус-вектором точки z и положительным направлением оси Ох.

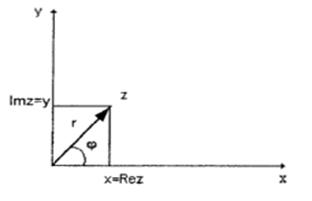
Очевидно, что если |z| = r, arg z = j, то действительная часть числа z Re z = x = r cosj, а мнимая часть числа z Jm z = y = r sin j.

Таким образом, в терминах модуля и аргумента комплексное число можно представить в виде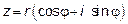

Для определения тригонометрической формы комплексного числа z найдём r,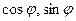

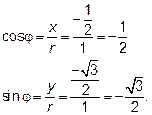
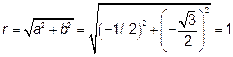
Та как sin и cos угла 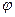отрицательны, делаем вывод, что угол находится в III четверти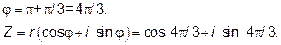

Вычислим по формуле Муавра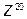

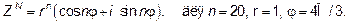
1²⁰=1

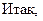
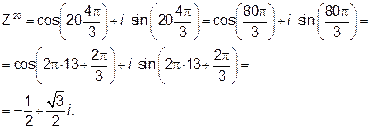
Пример 3. Решить уравнение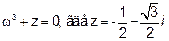

Известно, что корнем n - степени из числа z называется любое число , такое, что 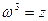и ω имеет n различных значений.

Решение: если число z представить в тригонометрической форме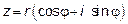

то значения 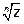м ожно представить формулой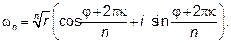

Поскольку все 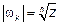одинаковы, а аргументы отличаются на 2П/n, то значения 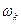на комплексной плоскости располагаются в вершинах правильного n угольника. Величина 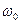называется главным значением корня

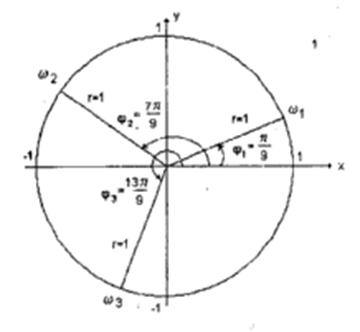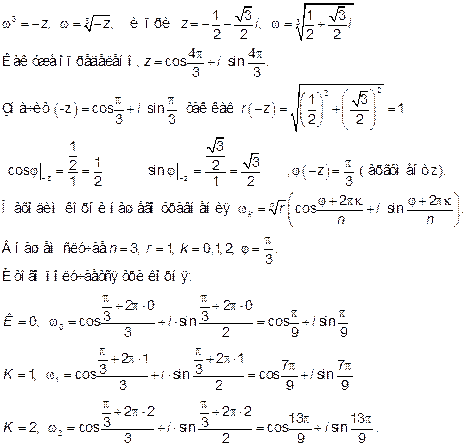
Итак, корнями уравнения будут три единичных вектора, расположенных под углом в 120 градусов друг к другу.

Решить самостоятельно следующие задачи:

9.1.Найти все значения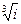

9.2.Найти все значения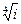

ЗАДАНИЕ №10

Для решения контрольной работы №2 по математике или контрольной работы №1 по математическому анализу (для специальности ЭВМ) надо изучить разделы, посвященные пределам функции одной переменной и ее производной.

Пределом функци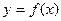и при 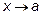называется число «а» такое, что для любого 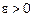можно найти такое число 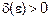, что для любого «x» из промежутка 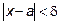будет выполняться неравенство 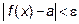. Имеют место следующие свойства пределов: при 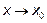, имеющие место и при :

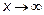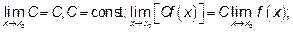
если существуют и не бесконечны 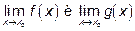, то

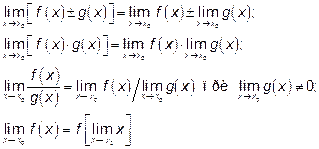
и следующие замечательные пределы

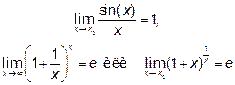
Решим задачи, подобные задачам из контрольной работы:

Пример 1. Найти предел L=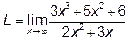

Решение: Имеем неопределённость вида .

Если к такой неопределённости сводится предел отношения двух

многочленов, при 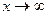следует в числителе и в знаменателе дроби вынести за

скобки самую высокую входящую в них степень аргумента, а затем сократить дробь.

Вынесем за скобки в числителе и знаменателе старшую степень

аргумента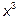

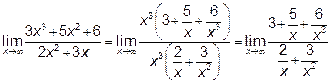
Так как 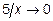и при 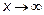, то предел числителя при

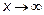равен 3. Предел знаменателя равен 0. Следовательно, предел

дроби равен .

Ответ: L=

Пример 2. Найти .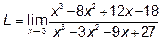

Решение: Здесь неопределённость вида 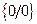.Если к такой

неопределённости сводится предел отношения двух многочленов при

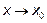, нужно и в числителе и в знаменателе выделить критический

множитель (x-x₀) и сократить на него числитель и знаменатель дроби.

Выделяем критический множитель (x-3)

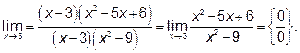
Опять возникла та же неопределённость. Действуя аналогично,

получаем:

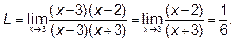
Ответ: .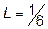

Пример 3. Найти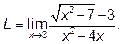

Решение: Неопределённость 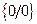. В этом случае нужно либо в

числителе, либо в знаменателе дроби избавиться от иррациональных

выражений, которые в точке 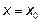обращаются в нуль.

Чтобы раскрыть эту неопределённость, умножим и разделим дробь

на выражение, сопряжённое числителю.

.

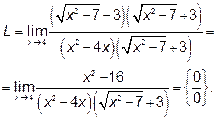Теперь неопределённость создаёт критический множитель .

Выделим его в числителе и знаменателе дроби, а затем сократим на него

числитель и знаменатель.

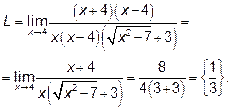
Ответ: L= .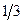

Пример 4. Найти пределы а) б) .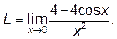

Решение: Неопределённость вида .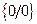

а) При 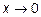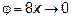. Умножая и числитель и знаменатель

дроби на 8, приведём заданный предел к первому замечательному пределу.

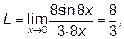
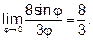
Иногда для раскрытия неопределённости приходится предварительно

применять тригонометрические формулы. В случае б) в числителе

воспользуемся формулой 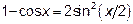и получим

Полагая 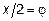и учитывая, что при 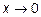, окончательно получим

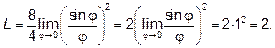
Ответ: а) 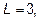, б) .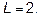

Пример 5. Найти предел .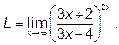

Решение: Неопределённость вида 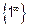.Для раскрытия этой неопределенности

используется второй замечательный предел.

Выделяем в круглых скобках целую часть

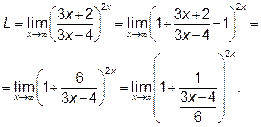
Обозначим . Если 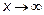, то и 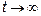. Далее показатель степени

умножаем и делим на .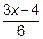

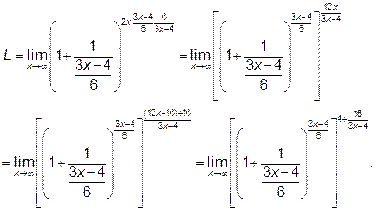
Делаем замену переменно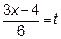й и 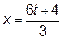. Находим предел

показателя степени

.

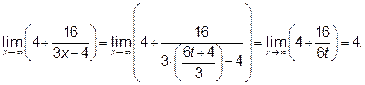
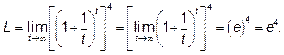Ответ: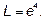

Более подробно о пределах функции можно почитать в [4] глава 2; [1] глава 8 и задачи о пределах можно найти в [3] гл.6 §4.

Дата добавления: 2014-12-10