Найти угол между прямыми

и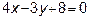

2.2 Даны уравнение двух сторон параллелограмма 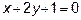(АВ) и (АD) и точка пересечения его диагоналей N(1,2). Найти уравнения двух других сторон этого параллелограмма.

ЗАДАНИЕ №3

Для решения третьей задачи потребуются следующие понятия о кривых второго порядка: Пусть на плоскости имеется прямоугольная декартова система координат. Как было видно в предыдущей задаче, множество точек плоскости, удовлетворяющих равенству =0 является линией.

В примере №2 уравнения были линейными(т.е.функция являлась многочленом первой степени), линия- прямой линией; то есть линиями первого порядка являлись прямые линии. В качестве функции может выступать и многочлен второй степени

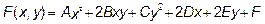
такое уравнение – уравнение линии второго порядка.

ЭЛЛИПС

Если уравнение имеет вид

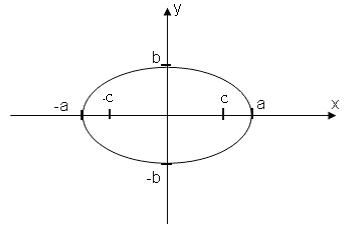
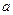то кривая называется эллипсом (каноническое уравнение эллипса). Точка -центр эллипса. Точки (± ,0),(0, ± 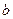) называются вершинами эллипса.

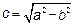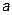( < ) – расстояние от центра до фокусов

Если 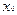= =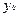0, то центр эллипса совпадает с началом координат и точки (- ,0) и (,0) –левый и правый фокусы эллипса.

Число называется эксцентриситетом эллипса.

ГИПЕРБОЛА

Если уравнение имеет вид

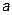>0, >0

кривая называется гиперболой (каноническое уравнение гиперболы )

Точка - центр гиперболы, Точки (± 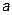,0)- вершины гиперболы, При 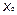=0, =0,

Прямые 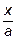= ± асимптоты гиперболы.

, >0. Точки (- ,0) и (,0) фокусы гиперболы.

ПАРАБОЛА

Если уравнение имеет вид:

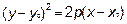, где 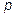>0, то линия называется параболой (каноническое

уравнение параболы)

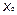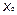, -координаты вершины параболы; При = =0 (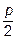,0) - фокус параболы; прямая

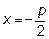- директриса параболы.

На плоскости может быть введена не только декартова прямоугольная, но и полярная система координат.

Зададим точку О -полюс, ось Z содержащую точку О и единицу длины оси Z.

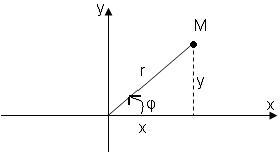
Возьмем произвольную точку М плоскости. Её положение на плоскости определяется двумя числами – расстоянием r от О до М (полярный радиус) и отсчитываемым против часовой стрелки углом φ между лучом OM и лучом оси (полярный угол). Если поместить начало координат декартовой прямоугольной системы в полюс, то координаты будут связаны следующим образом.

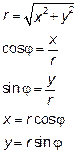
Пример 1. Пусть в задаче №3

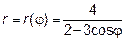
Построим заданную линию по точкам в полярной системе координат. В начале определим область допустимых значений (ОДЗ) независимой переменной φ. По определению полярной системы координат 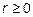и .Точке r = 0 соответствует полюс 0.

По условию задач угол φ может меняться от 0 до 2π. Поэтому наибольшие размеры ОДЗ таковы 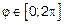. При этом r> 0 (r 0), т.к. числитель соответствующей дроби 4>0. отсюда знаменатель этой дроби также должен удовлетворять неравенству

2-3cos φ > 0 или cos φ < 2/3.

Решаем последнее неравенство

cos φ = 2/3 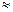0,667;

0,667 +2 πk, k 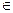N; φ = .

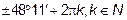В промежуток попадают два значения φ₁= и φ ₂ = - .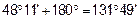

Отсюда для cos φ <2/3.

Следовательно допустимые значения φ принадлежат промежутку от 3 π /8 до 13 π /8, т.е. ОДЗ: .

Результаты расчетов заносим в таблицу

φ	3π/8	π/2	5π/8	6π/8	7π/8	π	9π/8	10π/8	11π/8	12π/8	13π/8
cos φ	0.38		-0.38	-0.71	-0.92	-1	-0.92	-0.71	-0.38		0.38
r	4.75		1.27	0.97	0.84	0.8	0.84	0.97	1.27		4.75

Строим чертеж,откладывая на луче, проведенном из полюса О под определенным углом φ, соответствующие значения радиус-вектора r из таблицы

rl(φ)

Для перехода к системе 0ху воспользуемся формулами. Имеем, следовательно

r (2-3cos φ)=4,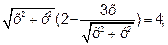

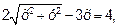
Определяем ОДЗ для х. Из ОДЗ: для φ 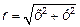>0.

Следовательно 3х+4>0. Отсюда ОДЗ: х >-4/3.

Возводим правую и левую части равенства в квадрат и выделяем полный квадрат для переменной х:

4 х ²+4 у ²=9 х ²+24 х +16;

(5 х ²+24 х)-4 у ²+16=0;

5(х ²+2 ;

(х +12/5)²-4/5 у ²-144/25+16/5=0;

(х+12/5)²-4у²/5=64/25

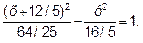
Окончательно получаем уравнение гиперболы

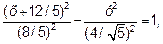х > -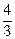

с центром в точке С(-12/5;0), а = 8/5, b = 4/ .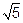

Находим координаты фокусов, уравнения асимптот и эксцентриситет. Для этого систему координат 0 ху параллельно перенесем в точку 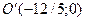. Заменяя переменные

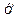= х +12/5, = у,

получим в новой системе координат 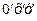уравнение гиперболы с центром в

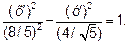
Получим координаты фокусов, уравнения асимтот и эксцентриситет гиперболы:

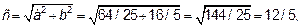
или ,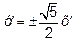

Переходим в старую систему координат. Имеем:

.

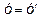Следовательно:

F₁(x;y)=F₁(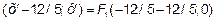 =F₁(-24/5;0);

F₂( 0;0), у = +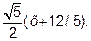

Совмещаем начало О системы координат Оху с полюсом, отмечаем координаты фокусов F ₁ и F ₂, проводим асимптоты и строим пунктиром левую ветвь гиперболы, т.к. точки гиперболы в полуплоскости слева от прямой х= -4/3 не удовлетворяют ОДЗ х >-4/3.

Более подробное описание кривых второго порядка смотрите в [1] гл.3; в [2] §24.

В случае если уравнение не подходит под один из перечисленных выше частных случаев линии второго порядка требование задачи «назвать линию» следует опустить.

Решение аналогичных задач можно найти в [3] гл.1 §3.

Решите самостоятельно задачи:

3.1 Привести к простейшему виду уравнение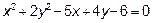

3.2 Уравнение асимптот гиперболы 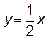и 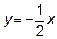, а расстояние между фокусами 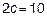. Найти уравнение гиперболы.

ЗАДАНИЕ №4

Для решения задачи № 4 следует иметь понятие о базисе.

Система из n линейно независимых векторов в n-мерном пространственазывается базисом. Векторы 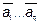называются линейно независимыми, если равенство

(линейная комбинация этих векторов равна 0) выполняется только при нулевых значениях коэффициентов 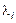– всех 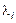при i=1,2…n.

Если это равенство имеет место при условии, что хотя бы один из коэффициентов 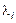отличен от нуля, то система векторов называется линейно зависимой.

В n -мерном пространстве линейно независимая система векторов не может содержать более n векторов.

Пусть задана система из n линейных уравнений с n неизвестными

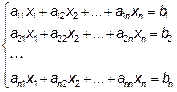
Матрица системы – набор из 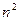чисел-коэффициентов системы, так как число строк матрицы равно числу столбцов матрица называется квадратной.

Её определитель (для случая, когда n=3):

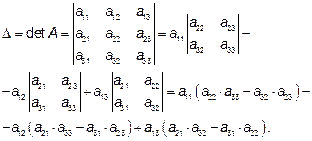
-определитель разложен по первой строке. Как определяются определители высших порядков, можно узнать в указанных ниже учебниках или в следующем разделе.

Итак, если определитель системы , то система имеет единственное решение , которое можно найти по формулам Крамера

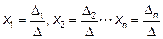
Где определитель матрицы системы, а 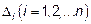определитель матрицы, полученной из матрицы системы А заменой i- го столбца на столбец свободных членов .

Пример 1. Решим задачу разложения вектора по базису:

Пусть даны вектора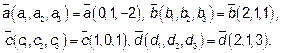

Решение.: Покажем в начале, что векторы 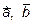и 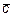образуют базис. Система векторов образует базис, если эти векторы линейно независимы, а соответствующее векторное уравнение

Обращается в тождество только при λ₁=λ₂=λ₃=0.

Используя координаты векторов 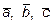, составим систему линейных уравнений, эквивалентную векторному уравнению

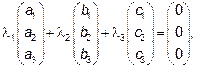
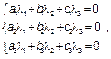
Вычисляем определитель Δ данной системы

=1(-1)-1(-2)=1.

Так как Δ 0, то система имеет только нулевое решение (λ₁,λ₂,λ₃) =(0,0,0). Это следует из того факта, что при b_i =0 все определители при неизвестных в формулах Крамера равны нулю Δ₁ = Δ₂ =Δ₃ = 0.

Следовательно, векторы 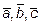образуют базис.

Найдем координаты вектора в базисе 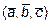. Четыре вектора в трехмерном пространстве всегда линейно зависимы, т.е. вектор есть линейная комбинация векторов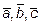

.

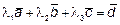Аналогично предыдущему случаю составим систему уравнений для определения координат λ₁,λ₂,λ₃ вектора в базисе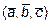

Определитель системы совпадает с определителем системы и не равен нулю Δ=1 0. Следовательно, система имеет единственное решение. По формулам находим λ₁,λ₂ и λ₃

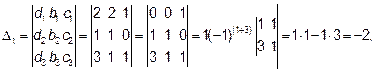
λ₁=Δ₁/Δ=-2/1=-2, λ₂=Δ₂/Δ=3/1=3, λ₃=Δ₃/Δ=-4/1=-4,

Итак, разложение вектора по базису 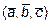имеет вид:

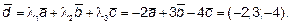
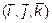Если векторы заданы в базисе , то в этом базисе вектор имеет координаты (2;1;3).

Студенту рекомендуется самостоятельно нарисовать векторы в пространстве R ³ и сравнить полученные значения λ_i cо значениями, полученными графически.

Следующую задачу решите самостоятельно:

Дата добавления: 2014-12-10