Формула полной вероятности. Формула Байеса

Примеры для самостоятельного решения

1. Ученик с вероятностью 0,01 делает ошибку А, с вероятностью 0,02 делает ошибку В и с вероятностью 0,005 делает обе ошибки. Найти вероятность того, что ученик сделает хотя бы одну ошибку. Ответ: 0,025.

2. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наудачу извлекают по одному шару. Какова вероятность того, что оба шара одного цвета? Ответ: 0,323.

3. Вероятность поражения цели первым стрелком при одном выстреле – 0,8, а вторым стрелком – 0,6. Найти вероятность того, что цель будет поражена только одним стрелком. Ответ: 0,44.

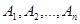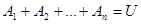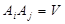Систему событий называют полной группой событий, если выполняются условия: 1) ; 2) при 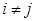. Это значит, что события полной группы попарно несовместны и в результате каждого испытания должно обязательно появляться одно из событий 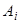. Обозначим 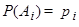, тогда

Другой пример. Проводится опыт, состоящий в бросании игральной кости. Пусть 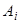─ событие, заключающееся в выпадении 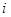очков на верхней грани этой кости, тогда события 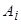− попарно несовместны ( 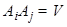при 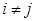) и в результате опыта обязательно должно появиться одно из событий 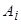(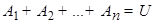). Значит, события 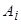составляют полную группу событий, чего нельзя сказать о событиях 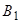− появление герба на первой монете и 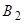− появление цифры на второй монете в опыте, состоящем в одновременном подбрасывании двух монет (этому мешает хотя бы совместность событи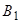й и ).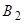

Формула полной вероятности является следствием теорем сложения и умножения вероятностей.

Пусть некоторое событие А происходит только с каким-нибудь одним из событий Н₁, Н₂, Н₃, …, Н_n, которые образуют полную группу событий и называются гипотезами. В этом случае событие А можно представить в виде: А=А⋅Н₁ + А⋅Н₂ + А⋅Н₃ + … +А⋅Н_n. Отсюда, применяя теоремы сложения и умножения вероятностей и учитывая, что гипотезы попарно несовместны, получим:

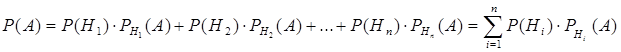, (8)

которая называется формулой полной вероятности. Используя формулы (6) и (8), можно получить формулу Байесса (формулу вероятности гипотез):

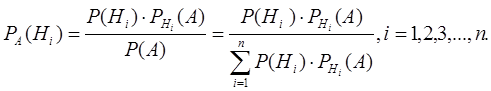(9)

События полной группы 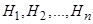обычно называют гипотезами. Их вероятности были известны до проведения опыта.

Пример. В районе имеется три кинотеатра. Вероятность того, что Света пойдет в первый кинотеатр, равна 0,5; во второй – 0,3; в третий – 0,2. Вероятность встретить Ирину в одном из этих кинотеатров равна соответственно 0,7; 0,5 и 0,3. Света пошла в кино. Найти вероятность того, что она встретит Ирину.

Решение: Обозначим А – событие, состоящее в том, что Света встретит Ирину в кинотеатре; Н₁ – встреча состоялась в первом кинотеатре, Н₂ -во втором, Н₃ – в третьем. Из условия задачи известны: Р(Н₁)=0,5; Р(Н₂)=0,3; Р(Н₃)=0,2, а также 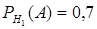, , 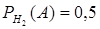. По формуле полной вероятности имеем:

Р(А) = 0,5⋅0,7 + 0,3⋅0,5 + 0,2⋅0,3 = 0,56. ♦

Пример. Данные из предыдущего примера. Известно, что Света встретила Ирину в одном из кинотеатров. Найти вероятность того, что встреча состоялась в первом кинотеатре.

Решение: Используя полученные выше результаты, по формуле (9) находим: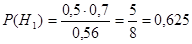

Пример. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим через 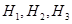гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

, , .

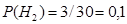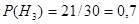Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи

, , .

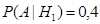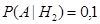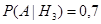По формуле полной вероятности получаем:

.

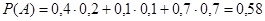Пример. Данные из предыдущего примера. Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?

Решение. Вероятность получить «неуд» равна . Требуется вычислить условные вероятности. По формулам Байеса получаем:

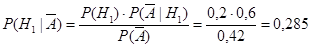, и аналогично,

,

.

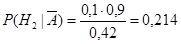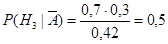Отсюда следует, что, вероятнее всего, слабо подготовившийся студент сдавал экзамен третьему экзаменатору.

Пример. Была проведена одна и та же контрольная работа в трех группах. В первой группе из 30 студентов 8 выполнили работу на «отлично», во второй, где 28 студентов, – 6 «отличных» работ, в третьей, где 27 студентов, – 9 работ выполнены на «отлично». Найти вероятность того, что первая выбранная наудачу работа из работ, принадлежащих группе, которая также выбрана наудачу, окажется «отличной».

Решение: Имеем три гипотезы: H 1 – выбрана работа из 1-й группы, H 2 – выбрана работа из 1-й группы, H 3 – выбрана работа из 1-й группы. Очевидно, что

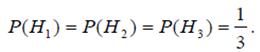
Обозначим искомое событие A – выбрана работа, выполненная на «отлично». Определим по классической формуле условные вероятности:

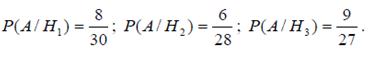
Отсюда по формуле полной вероятности

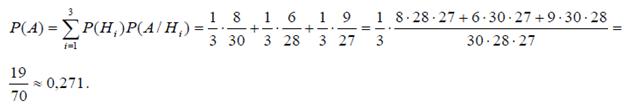
Пример. В группе из 10 студентов, пришедших на экзамен, 3 студента подготовлены отлично, 4 - хорошо, 2 - удовлетворительно и 1 - плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный - на 16, удовлетворительно подготовленный - на 10, плохо подготовленный - на 5. Вызванный наугад студент ответил на все три заданных преподавателем вопроса. Найти вероятность того, что этот студент: а) подготовлен отлично; б) подготовлен плохо.

Решение. Пусть событие А={студент ответил все три вопроса}. Введем систему гипотез:

H 1={студент подготовлен отлично};

H 2 ={студент подготовлен хорошо};

H 3={студент подготовлен удовлетворительно};

H 4 ={студент подготовлен плохо}.

Находим вероятности гипотез: P (H 1) = 0,3; P (H 2) = 0,4; P (H 3) = 0,2; P (H 4) = 0,1.

Находим условные вероятности события А.

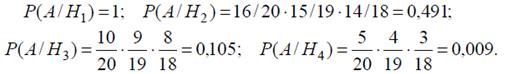
По формуле Байеса находим

Ответ: 0,58; 0,002.

Дата добавления: 2014-12-10