Примеры для самостоятельного решения

1. Имеется два набора пластилина. Вероятность того, что кусок пластилина из первого набора не имеет дефектов, равна 0,8, а из второго – 0,9. Найти вероятность того, что взятый наудачу кусок пластилина (из наудачу взятого набора) – не имеет дефектов. Ответ. 0,85.

2. При отклонении от нормы режима работы автомата срабатывает сигнализатор 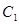с вероятностью 0,8, а 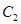с вероятностью 1. Вероятность того, что автомат снабжен сигнализатором 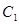, равна 0,6, а 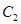- 0,4. Получен сигнал о разладке автомата. Что вероятнее: автомат снабжен сигнализатором 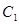или 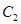? Ответ: Вероятнее, что автомат снабжен сигнализатором .

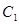Схема решения задач по теории вероятности.

1) Прежде чем перейти к определению вероятности с помощью теорем о сложении и умножении вероятностей проверьте нельзя ли использовать классическое или геометрическое определение вероятности.

2) Определите не идет ли в задаче речь о ситуациях с полной группой событий (применяем формулу полной вероятности) или и о вероятности гипотез (применяем формулу Баейса).

3) Определить главное событие вероятность, которого требуется найти по условию задачи.

4) Определить составные события, как составные части главного события.

5) Определить связь между составными событиями: «И», «ИЛИ».

6) Если связь – «И», можно применять теоремы для произведения событий.

7) Если связь – «ИЛИ», можно применять теоремы для суммы событий.

8) При применении теоремы для произведения событий необходимо проверить события на зависимость и применять соответствующую теорему.

9) При применении теоремы для суммы событий необходимо проверить события на совместимость и применять соответствующую теорему.

Дата добавления: 2014-12-10