Правило вычисления вероятности по размеченному вероятностному графу

Решение задач по теории вероятности с помощью графов.

Одним из самых наглядных способов решения задач по теории вероятности служит применение размеченных графов или деревьев вероятности.

Размеченный граф вероятностей рисуют (как правило) слева направо. Опыты [испытания] обозначаются в виде жирных точек (рис. 1 и 2) или в виде прямоугольников (рис. 3 – 12), а каждый исход – сплошной линией (ветвью), идущей от соответствующей точки или прямоугольника. Около каждой ветви указывается вероятность соответствующего исхода. Сумма вероятностей на ветвях, выходящих из одного прямоугольника, равна единице. Двигаясь по ветвям и перемножая соответствующие вероятности, в конце пути мы получаем вероятность сложного события. Сложив нужные вероятности, найдем вероятность искомого события.

Имеется две основные разновидности графов: неориентированные и ориентированные. Неориентированный граф – совокупность точек (вершин графа) с соединяющими некоторые из них отрезками (ребрами графа; ветвями). Ориентированный граф – это совокупность точек (вершин) с соединяющими некоторые из них ориентированными отрезками (стрелками). В этой работе мы будем пользоваться только ориентированными графами.

1) вероятность попадания в конечную вершину (вероятность исхода) можно вычислить, перемножая вероятности, встречаемые на ребрах соответствующего маршрута (рис. 1, жирный маршрут);

2) если же нас интересует вероятность события, которому благоприятствуют несколько исходов, то вероятности соответствующих конечных вершин складываются (рис. 2, жирные маршруты).

Рисунок 1.

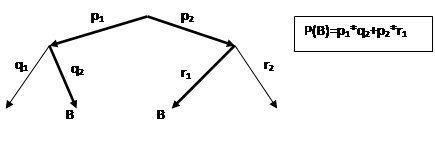Рисунок 2.

Пример. В каждой из трех групп по 25 студентов. Число студентов группы, сдавших экзамен по математике, равно 22, 20 и 18 соответственно. Случайно выбранный студент сдал экзамен по математике. Какова вероятность, что это студент первой группы?

Решение: Построим размеченный вероятностный граф

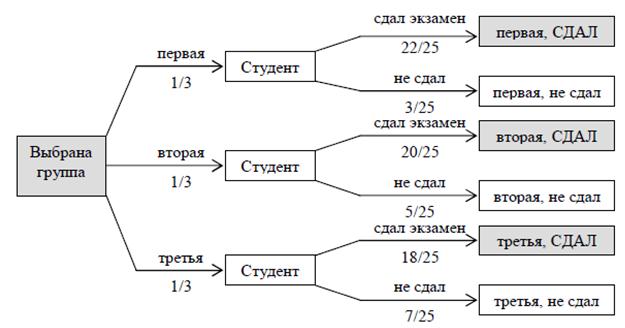
Обозначим через A событие, заключающееся в том, что случайно выбранный студент сдал экзамен. Этому событию на графе благоприятствуют три маршрута. Поэтому

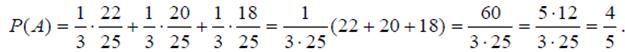
Пример. Студент пришел на экзамен, зная 25 из 30 билетов. Какова вероятность того, что он сдаст экзамен, если после отказа отвечать на билет ему предоставляется возможность вытянуть еще один?

Решение: Построим размеченный вероятностный граф

Обозначим через A событие, состоящее в том, что студент сдал экзамен. На графе вероятностей этому событию благоприятствуют два маршрута. Следовательно,

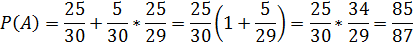
Пример. В первой урне находятся 7 белых и 9 черных шаров, во второй - 6 белых и 4 черных шаров. Из первой урны во вторую переложили два шара, а затем из второй урны извлекли один шар. Найти вероятность того, что этот шар белый.

Решение: Построим размеченный вероятностный граф

Пусть событие A - извлеченный из второй урны шар оказался белым. Этому событию на графе благоприятствуют четыре маршрута. Поэтому

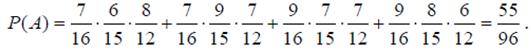
Задания для самостоятельной работы

Деканат решил проконтролировать посещение лекции по математике четырьмя нерадивыми студентами. Каждый из них может быть или не быть на этой лекции. Рассматриваются события:

A − на лекции был ровно один из 4 студентов;

B − на лекции был хотя бы один из студентов;

C − на лекции было не менее 2 студентов;

D − на лекции было ровно 2 студента;

E − на лекции было ровно 3 студента;

F − на лекции были все 4 студента.

Описать события:

1) A + B; 2) A*B; 3) B + C; 4) B*C; 5) D + E + F; 6) B*F.

Совпадают ли события B*F и C*F? B*C и D?

1. В урне 10 белых и 8 черных шаров. Наудачу выбрали 5 шаров. Найти вероятность того, что среди них окажется ровно 3 белых шара

2. Экзаменационный билет содержит два вопроса, а число всех билетов равно двадцати. Студент знает ответы на 20 вопросов программы. Какова вероятность получить положительную оценку, если она ставится при условии, что студент ответит хотя бы на один вопрос билета, а число билетов, которые студент знает полностью, равно восьми?

3. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «юрта».

4. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.

5. На первом этаже семиэтажного дома в лифт зашли 3 человека. Вероятности выхода каждого из лифта на любом этаже одинакова. Найти вероятность того, что все трое вышли из лифта на 4 этаже.

6. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.

7. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово «кукла»?

8. В урне 4 белых и 4 черных шара. Из этой урны наудачу извлекли 5 шаров. Какова вероятность того, что 2 из них белые, а 3 – черные?

9. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

10. События A, B, C и D образуют полную группу событий. Вероятности событий таковы: P(A) = 0,1; P(B) = 0,4; P(C) = 0,3. Чему равна вероятность события D.

11. Школьная библиотека получила 3 коробки учебников русского языка, напечатанных в типографии № 1, и 2 коробки учебников, напечатанных в типографии № 2. Вероятность того, что учебник из типографии № 1 не имеет опечаток, равна 0,8, а типографии № 2 – 0,9. Учительница наудачу извлекает учебник из наудачу выбранной коробки, и дает его Андрею. Найти вероятность того, что у Андрея учебник без опечаток.

12. На пяти одинаковых карточках написаны буквы: на двух карточках "л", на остальных трех "и". Вкладываем наудачу эти карточки подряд. Какова вероятность того, что при этом получится слово "лилии"?

13. Четырёхтомное сочинение расположено на полке в произвольном порядке. Какова вероятность, что номера томов идут подряд?

14. В двух ящиках находятся детали: в первом – 10 (из них 3 стандартных), во втором – 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.

15. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей группы – 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?

16. Из 5 букв разрезанной азбуки составлено слово - КНИГА. Неграмотный мальчик перемешал буквы, а потом наугад их собрал. Какова вероятность того, что он опять составил слово КНИГА?

17. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из трех человек. Какова вероятность того (если считать выбор случайным), что выбраны две девочки и один мальчик.

18. Для кабинета физики покупают микроскоп. В магазине есть в наличие 4 модели микроскопа. Вероятности того, что микроскоп определенной модели выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что наудачу купленный микроскоп выдержит гарантийный срок службы.

Дата добавления: 2014-12-10