Возрастание и убывание функции

Задания для контрольной работы.

Выбор номеров вопросов определяется последней цифрой.

Задание 1. Вычислить пределы:

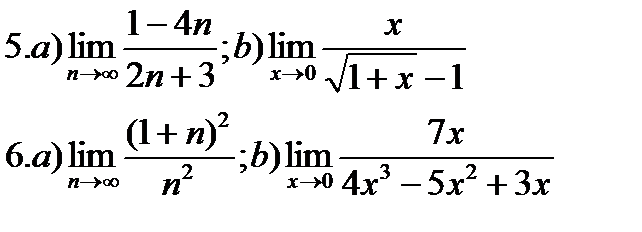
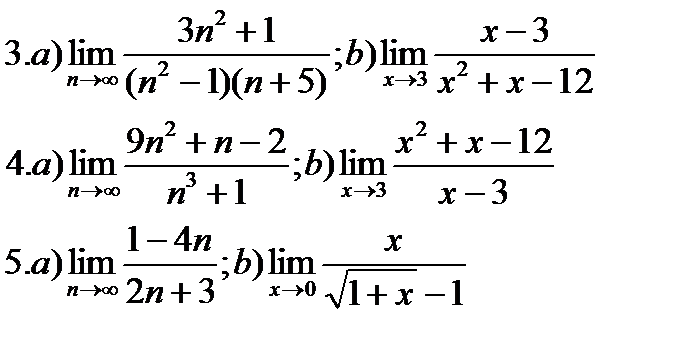
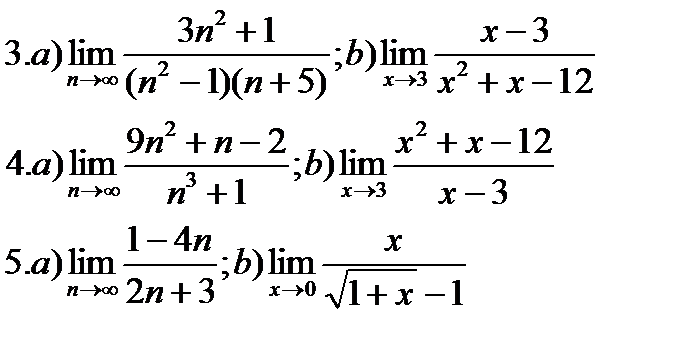
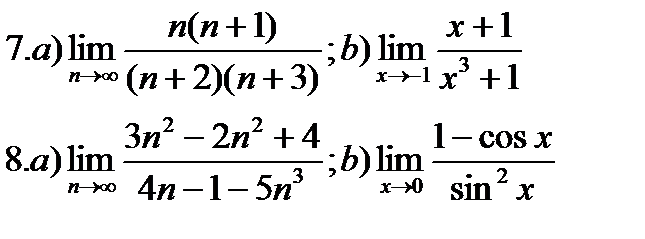
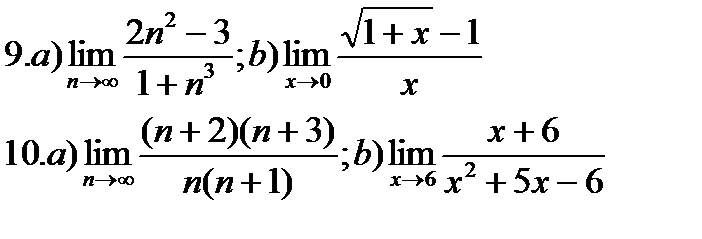
Указания к заданию 1

Опр.Число А называется пределом функции f (x) при х, стремящемся к х_о (или в точке х_о),

если для любого 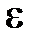> 0 существует такое , что для всех х, удовлетворяющих

условиям | х – х_о | < 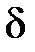, х ¹ х ₀, имеет место неравенство | f (x) – А| < .

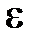Если А есть предел функции f (x) при х, стремящемся к х_{о ,} то пишут

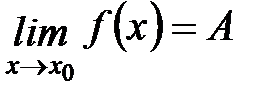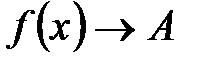или при .

Если в определении предела вместо неравенств 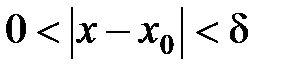, т.е. ,

х ¹ х₀, рассмотреть неравенства 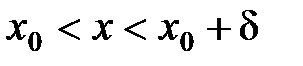, то получим понятие правого предела. В

этом случае пишут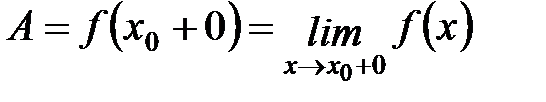

Рассматривая неравенства , вводим понятие левого предела:

.

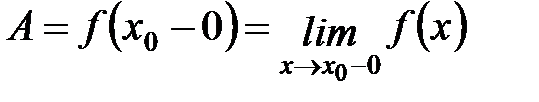Предел (двусторонний) функции в точке х_о существует в том и только в том случае, когда левый и правый пределы в этой точке существуют и совпадают: f (x₀ –0)= f (x₀ +0).

Опр. Число А называется пределом функции f (x) при x ® +¥, ,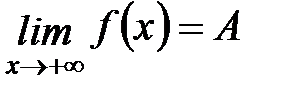

если для любого 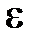>0 существует такое М>0, что х > М Þ | f (x) – А | < .

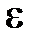Опр. Число А называется пределом функции f (x) при x ® -¥, ,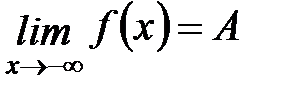

если для любого 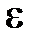>0 существует такое М>0, что х < –М Þ | f (x) – А | < .

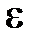Опр. Число А называется пределом функции f (x) при x ® ¥, ,

если для любого 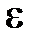>0 существует такое М>0, что | х | > М Þ | f (x) – А | < .

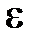Замечание: вычисление любого предела начинается с подстановки предельного значения аргумента в функцию стоящую под знаком предела.

Пример 1. Вычислить предел

Пример 2. Вычислить предел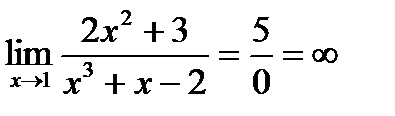

Пример 3. Вычислить предел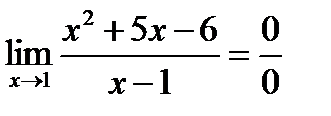

Решение. Если подставить х = 1 в рассматриваемую функцию, получим 0 в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностями, которые могут иметь вид: 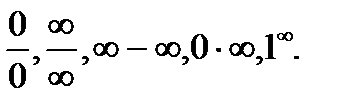Для каждой неопределенности существуют свои способы вычисления пределов.

Разложим числитель на множители: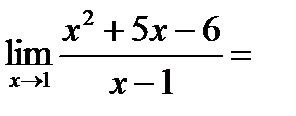

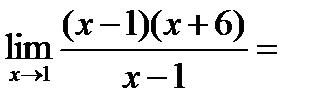
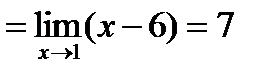
Замечание: а) замечательные пределы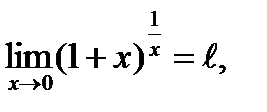

б) эквивалентности при 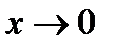sin , , ,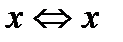

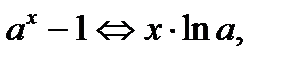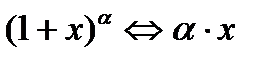. При вычислении пределов можно пользоваться этими соотношениями.

Пример 4. Вычислить предел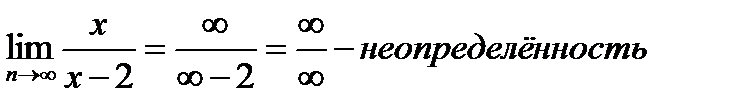

Необходимо разделить числитель и знаменатель на переменную в наивысшей степени:

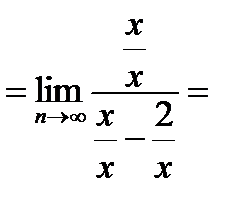
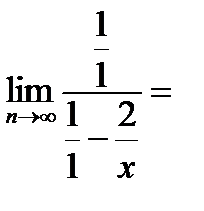
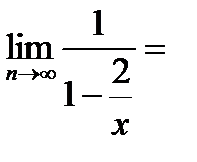
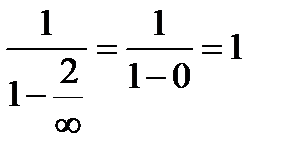
Задание 2. Производная и её приложения.

1. Найти производные функций:

Найти интервалы выпуклости и точки перегиба графика функции: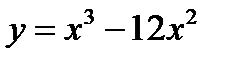

2. Найти производные функций: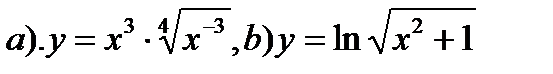

Найти наименьшее и наибольшее значения функции:

3. Найти производные функций: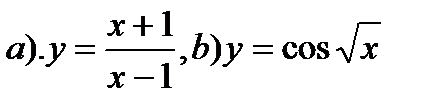

Исследовать функцию на монотонность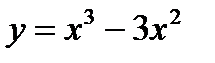

4. Найти производные функций: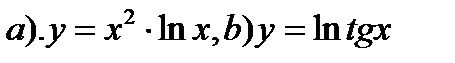

Исследовать функцию на экстремум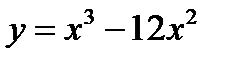

5. Найти производные функций:

Найти наименьшее и наибольшее значения функции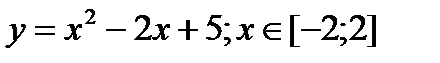

6. Найти производные функций: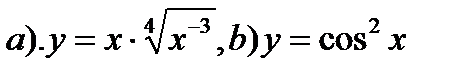

Исследовать функцию на монотонность: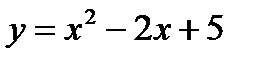

7. Найти производные функций:

Найти интервалы выпуклости и точки перегиба графика функции:

8. Найти производные функций: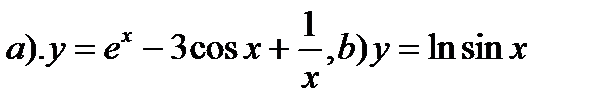

Исследовать функцию на монотонность:

9. Найти производные функций: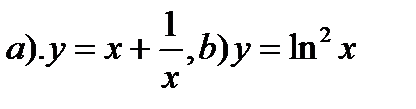

Исследовать функцию на экстремум: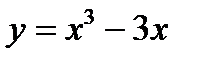

10. Найти производные функций:

Найти наименьшее и наибольшее значения функции:

Указания к заданию 2

Опр. Если при существует конечный предел дроби , то этот предел называют производной функции в точке х и обозначают символом :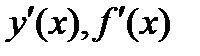

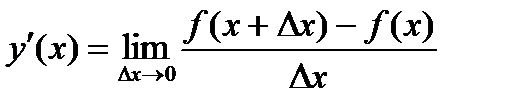
Основные правила и формулы дифференцирования

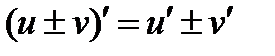
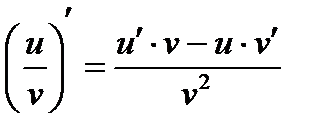
Формулы:

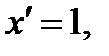
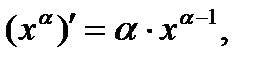
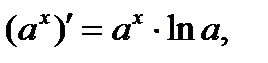
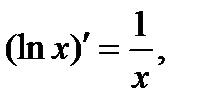
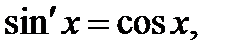
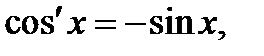
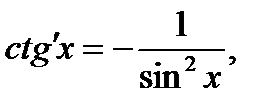
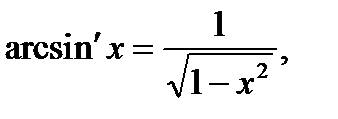
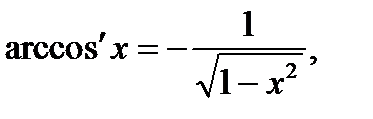
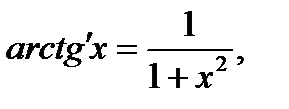
Для того чтобы дифференцируемая функция f(x), возрастала в некотором промежутке, необходимо и достаточно, чтобы ее производная была неотрицательна в этом промежутке, f’(x)≥0.

Для того чтобы дифференцируемая функция f(x) убывала в некотором промежутке, необходимо и достаточно, чтобы ее производная была не положительна в этом промежутке, f(x)≤0.

Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции, необходимо:

1). Найти область определения функции.

2). Найти производную функции.

3). Приравнять производную к нулю, го есть определить ее корни, а также найти точки, в которых производная не существует, а функция существует.

4). Определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.

Пример: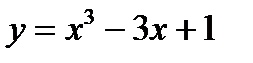

1.Область определения – любое число.

2. Найдём производную: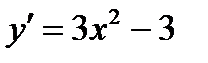

3. 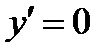если 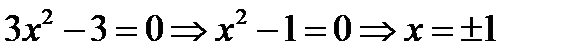. Точек в которых функция не существует нет.

4. -1 1

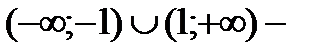функция возрастает, 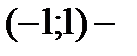функция убывает.

Дата добавления: 2014-12-10