
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопросы. Исследование функций и построение графиков
|
|
|
|
Исследование функций и построение графиков
Производная и дифференциал функции.
Цель занятия: Научиться находить производные основных элементарных функций, уметь исследовать функции с помощью производной.
1. Понятие производной.
2. Правила дифференцирования. Формулы дифференцирования.
3. Дифференциал функции.
4. Возрастание и убывание функции.
5. Экстремумы функции. Условия экстремума функции.
6. Выпуклость и вогнутость графика функции. Точки перегиба.
7. Построение графиков функций.
Решение типовых задач
1. Найти производные следующих функций:
а) 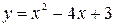 ; б)
; б) 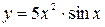 ; в)
; в)  .
.
Решение. Вычислим производные данных функций:
а) 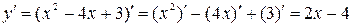 .
.
б) 
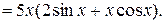
в) 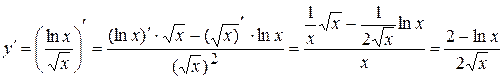 .
.
2. Найти производные функций:
а) 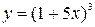 ; б)
; б) 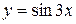 .
.
Решение. а) 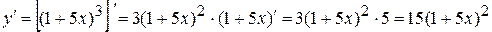 .
.
б) 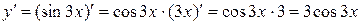 .
.
3. Найти производную 2-ого порядка от функции 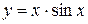 .
.
Решение.  . Дифференцируя производную
. Дифференцируя производную 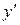 , получаем:
, получаем: 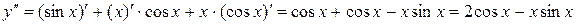 .
.
4. Найти дифференциалы функции:
а) 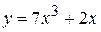 ; б)
; б) 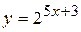 .
.
Решение. а) Вычислим производную функции:
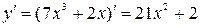 .
.
Дифференциал функции найдем по формуле 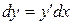 :
:
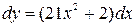 .
.
б) Вычислим дифференциал по аналогии с предыдущим примером:
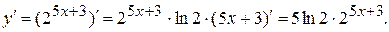
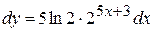 .
.
5. Исследовать функцию 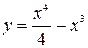 и построить ее график.
и построить ее график.
Решение.
1. Область определения функции: 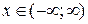 .
.
2. Функция не является ни четной, ни нечетной.
3. Точки пересечения с осями координат.
Пусть 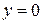 , тогда
, тогда 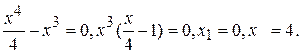 ;
;
График пересекает ось Ох в точках 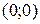 и
и 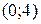 .
.
4. Найдем интервалы возрастания и убывания и экстремумы функции.
Найдем 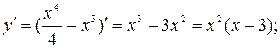
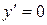 при
при  и
и 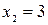 .
.
Выясним знак 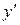 в окрестности критических точек.
в окрестности критических точек.

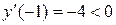
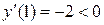
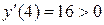
При переходе через точку 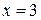 производная
производная 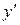 меняет знак с минуса на плюс, следовательно,
меняет знак с минуса на плюс, следовательно, 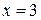 - точка минимума функции.
- точка минимума функции.
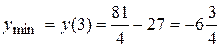 .
.
Функция убывает на интервале на 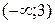 и возрастает на интервале
и возрастает на интервале 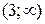 .
.
5. Найдем интервалы выпуклости и вогнутости функции и точки перегиба.
Найдем производную второго порядка
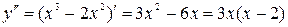 ;
;

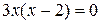 ,
, 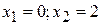 .
.
Исследуем знак 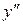 в окрестности точек
в окрестности точек 
 и
и 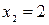 .
.

В интервале 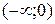 кривая вогнута, в интервале
кривая вогнута, в интервале 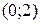 кривая выпуклая, в интервале
кривая выпуклая, в интервале 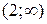 кривая вогнута.
кривая вогнута.
Итак, при переходе через точки 
 и
и 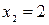 вторая производная меняет знак. Следовательно, кривая имеет две точки перегиба:
вторая производная меняет знак. Следовательно, кривая имеет две точки перегиба: 
 и
и 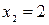 . Найдем ординаты точек перегиба
. Найдем ординаты точек перегиба
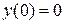 ;
; 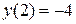 .
.
6. 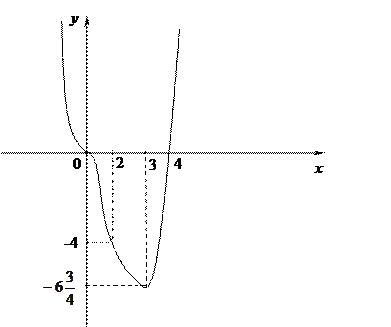 Построим график функции
Построим график функции
Задания для самостоятельного решения
1. Найдите производные и дифференциалы указанных функций:
1. 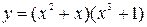 ;
; 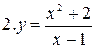 ;
;
3. 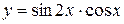 ; 4.
; 4. 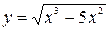 ;
;
5.  ; 6.
; 6.  .
.
2. Найдите значение производной функции 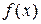 в заданной точке
в заданной точке 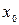 :
:
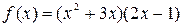 ,
, 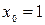 .
.
3. Найдите производные второго порядка функций:
а) 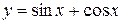 ; б)
; б) 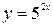 .
.
4. Определите точки экстремума функций:
1) 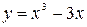 ; 2)
; 2)  .
.
5. Исследуйте функцию и постройте ее график
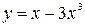 .
.
ЗАНЯТИЕ 5 (4 часа)
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 646; Нарушение авторских прав?; Мы поможем в написании вашей работы!