Решение типовых задач

1. В ящике находятся три белых и два черных шара. Из ящика вынимается наудачу один шар. Найти вероятность того, что этот шар будет белым.

Решение. Событие, состоящее в появлении белого шара, обозначим через А.

Общее число случаев .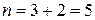

Число случаев, благоприятствующих событию А, .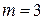

Тогда: .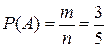

2. В урне находится 10 белых и 6 черных шаров. Из урны наудачу вынимаются два шара. Найти вероятность того, что оба шара будут белыми.

Решение. Обозначим через А событие, состоящее в появлении двух белых шаров.

Общее число возможных случаев

.

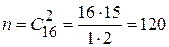Число случаев, благоприятствующих событию А

.

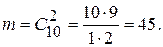
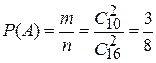3. В партии из 10 деталей 7 стандартных. Найдите вероятность того, что среди шести наудачу взятых деталей 4 стандартных.

Решение. Общее число возможных исходов 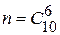. Подсчитаем число исходов, благоприятствующих интересующему нас событию: четыре стандартные детали можно взять из семи стандартных деталей 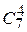способами; при этом остальные 6-4=2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10-7=3 нестандартных деталей можно 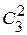способами.

Следовательно, число благоприятствующих исходов равно

.

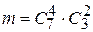Искомая вероятность равна

.

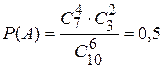4. Три стрелка стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,75, вторым стрелком – 0,8, третьим стрелком – 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель.

Решение. .

События А,В,С – независимые.

Применяем теорему умножения вероятностей:

.

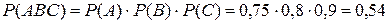5. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет только один стрелок.

Решение. Вероятность того, что в мишень попадет первый стрелок и не попадет второй, равна

.

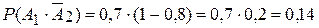Вероятность того, что попадет второй стрелок в мишень и не попадет первым равна:

.

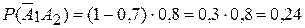Вероятность того, что в мишень попадет только один стрелок, равна сумме этих вероятностей:

.

6. Устройство содержит три независимо работающих элемента. Вероятности отказа элементов соответственно равны: 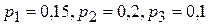. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

Решение.

;

;

;

.

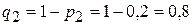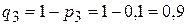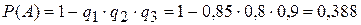7. Для некоторой местности среднее число ясных дней в июле равно 25. Найти вероятность того, что первые два дня июля будут ясными.

Решение.

Событие А – был солнечный день 1-ого июля;

Событие В – был солнечный день 2-ого июля.

При этом события А и В зависимы.

.

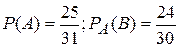По теореме умножения вероятностей зависимых событий получаем

.

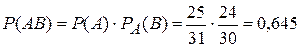8. На предприятии работают две бригады рабочих: первая производит в среднем 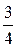продукции с процентом брака 4%, вторая - 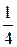продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие:

а) окажется бракованным;

б) изготовлено второй бригадой при условии, что изделие оказалось бракованным.

Решение.

а) Событие А – взятое наудачу изделие бракованное. Рассмотрим две гипотезы:

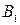- изделие изготовлено первой бригадой;

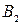- изделие изготовлено второй бригадой.

; .

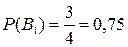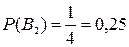Условные вероятности события А соответственно равны:

; .

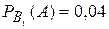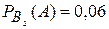Искомую вероятность 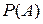найдем по формуле полной вероятности:

.

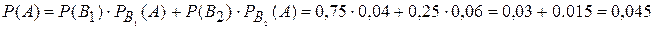б) Для определения вероятности того, что бракованное изделие изготовлено второй бригадой, воспользуемся формулой Байеса:

.

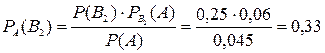Задания для самостоятельной работы

1. Монета подбрасывается дважды. Найдите вероятность того, что при этом герб выпадет:

а) только один раз;

б) хотя бы один раз;

в) два раза.

2. Из 60 вопросов, входящих в экзаменационные билеты, студент знает 50. Найти вероятность того, что среди 3-х наугад выбранных вопросах студент знает:

а) все вопросы;

б) два вопроса.

3. Вероятность того, что в течение одного рабочего дня возникнет неполадка в определенном приборе, равна 0,05. Какова вероятность того, что не произойдет ни одной неполадки за 3 рабочих дня?

4. В одном аквариуме находятся 3 белые, 3 красные и 3 голубые рыбки. Трех случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что все 3 рыбки белые?

5. Студент изучает биологию, химию и физику. Он оценивает, что вероятность получить «пятерку» по этим предметам равна соответственно:

; ; .

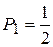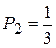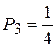Пусть оценки по этим предметам независимы. Какова вероятность, что он:

1) не получит ни одной «пятерки»?

2) получит «пятерку» только по биологии?

6. Отдел технического контроля проверят изделие на стандартность. Вероятность того, что изделие стандартно равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

7. В партии из 80 банок консервов оказалось три помятых. Какова вероятность того, что среди трех подряд взятых банок окажется хотя бы одна помятая?

8. Имеются три партии ламп по 20, 30, 50 штук в каждой. Вероятность того, что лампы проработают заданное время, равна для каждой партии соответственно 0,7; 0,8; 0,9. Какова вероятность того, что выбранная наудачу лампа из ста данных ламп проработает заданное время?

Литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисление. – М., Наука, 1985.

2. Ефимов Н.В. Краткий курс аналитической геометрии. – М., Наука, 1975.

3. Минорский В.П. Сборник задач и упражнений по высшей математике. – М., Изд-во физ. – мат. лит., 2001.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М., Высшая школа, 1997.

5. Гмурман В.Е. Теория вероятностей и математическая статистика. – Высшая школа., М., 2000.

6. Лихолетов И.И., Мацкевич П.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск, Высшая школа, 1976.

7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М., Высшая школа, 2000.

Дата добавления: 2014-12-16