
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над множествами
|
|
|
|
Практическое занятие №1. Операции над множествами
По математике
Электронный практикум
для студентов юридического факультета
Краснодар-2013
| Цель занятия: | 1. | изучить способы задания множеств; |
| 2. | получить навыки в применении операций над множествами. |
Множества можно задавать двумя способами:
1.перечислением элементов множества.
Например, множество M={x, y, z} состоит из трёх элементов, порядок перечисления которых не имеет значения, т.е. {x, y, z}={y, x, z}=...
2. описанием элементов множеств:
- описанием характеристических свойств, объединяющих элементы в виде уравнений, диаграмм Эйлера-Венна и геометрически. Например, множество M = {x2 Î N; x – простое число} задано квадратами простых чисел.
- описанием множеств, порожденных процедурами над элементами, означает указание алгоритма порождения элементов этого множества. Например, подмножество М всех нечетных натуральных чисел с помощью порождающей процедуры имеет вид: M={xÎN: x=1+2n, nÎN}
| Рассмотрим операции над множествами в порядке убывания приоритета. Пересечением (произведением) двух множеств называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно. Обозначение: С = АìüВ |
 | ||
| Объединением (суммой) двух множеств А и В называется множество С, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В (или тому и другому вместе). Обозначение: С = АîþВ |
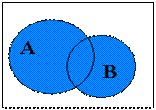
| ||
| Разностью множеств А и В называется такое множество С, которое состоит из тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В. Обозначение: С = А ½ В или С = А \ В |
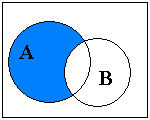
| ||
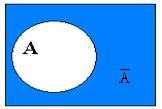
Дополнением множества А до универсального множества U называется множество С, равное разности U½A.
Обозначение: С = U½А или С = 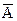 Симметрической разностью двух множеств А и В называется множество
Симметрической разностью двух множеств А и В называется множество
| 
| ||
| С = Аîþ В | Аìü В. Обозначение: С = А D В Формула включений и исключений для двух множеств А и В: n(АîþВ)= n(А)+ n(В) - n(А∩В). для трех множеств А, В и С: |
|
n(АîþВîþС)= n(А)+ n(В)+ n(С)- n(А∩В)-n(А∩С)-n(В∩С)-n(А∩В∩С)
где n(Z) – количество элементов множества Z, т.е. его мощность.
Примеры выполнения заданий
1. Заданы множества: А = {1, 3, 5, 7, 9}, B = {1, 2, 3, 4, 5}.
Найдите элементы множеств: D = Аîþ В и Е = АìüВ.
D= {1, 2, 3, 4, 5, 6, 7,8, 9}, Е = {1, 3, 5}.
Задания для самостоятельного выполнения
1. Задайте множество А перечислением его элементов:
| 0)A={xÎR| (x2–6x+5)×(x2–x–12)=0} | 1)A={xÎR |(x2–5x+6)×(x2+x–20)=0} |
| 2)A={xÎR| (x2 –5x +4)×(x2–x–6)=0} | 3)A={xÎR|(x2+4x–5)×(x2–7x+12)=0} |
| 4)A={xÎR| (x2+3x–4)×(x2+x–12)=0} | 5)A={xÎR |(x2–5x–6)×(x2–x–6)=0} |
| 6)A={xÎR |(x2 +x–2)×(x2–7x+6)=0} | 7)A={xÎR|(x2–3x–4)×(x2–9x+20)=0} |
| 8)A={xÎR |(x2–3x+2)×(x2–4x–5)=0} | 9)A={xÎR |(x2–x–2)×(x2–x–20)=0} |

2. Заданы множества: А = {1, 3, 9, 10, 8}, B = {5, 3, 11, 4, 8} и C = {1, 4, 8, 9, 10}. Найдите элементы множеств Д и Е:
| 0)Д = АîþВìüС; Е = (А D В) | С; | 1)Д = (АîþС) | (ВìüС); Е = А| ВìüС; |
| 2)Д = АîþВîþС; Е = АìüС D В; | 3)Д = (АîþС)ìüВ; Е = А DВîþС; |
| 4)Д = (АîþС) | В; Е = (В D С) | А; | 5)Д = АìüВìüС; Е = С D В | А; |
| 6)Д = Аîþ(В D С); Е = А | В | С; | 7)Д = (ВîþС) | (АìüС); Е = АîþВ | С; |
| 8)Д = (АîþВ)ìüС; Е = А D В | С; | 9)Д = (АîþВ) D С; Е = АìüВ | С; |

3. Изобразите с помощью диаграмм Эйлера-Венна в двух вариантах расположения следующие множества:
0) а)U½  ;
б) ;
б) 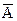 ìü B½C; ìü B½C;
| 1) а)CîþА½ 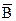 ;
б)(А½В)îþC; ;
б)(А½В)îþC;
| 2) а) (A D В)½C;
б) 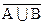 ìüС; ìüС;
|
| 3) а)АìüВ½С; б)AìüВîþС½А; | 4) а) 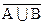 ½С;
б)(В½А)ìüC; ½С;
б)(В½А)ìüC;
| 5) а) 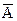 ìü ìü 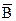 ½С;
б) ½С;
б) 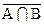 ½С; ½С;
|
6) а)С½АîþВ;
б) 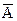 ìü (В D С); ìü (В D С);
| 7) а)U½ 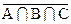 ;
б)CìüА½ ;
б)CìüА½ 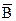 ; ;
| 8) а)A½ (B D C); б)С½АìüВ; |
| 9) а) (АîþВ)ìü(В D С); б)AîþВ½C; |
а)

б)

Законы теории множеств
| АîþВ | º ВîþА; | AîþÆ | º А; |
| АìüВ | º ВìüА; | AìüÆ | º Æ; |
| Аîþ (ВîþС) | º (АîþВ)îþ С; | Aìü 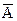
| º Æ; |
| Аìü (ВìüС) | º (АìüВ)ìüС; | AîþA | º А; |
| Аìü (ВîþС) | º (АìüВ)îþ (АìüС); | AìüA | º А; |
| Аîþ (ВìüС) | º (АîþВ)ìü(АîþС); | 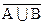
| º 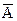 ìü ìü 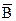 ; ;
|
| Аîþ U | º U; | 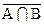
| º 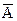 îþ îþ 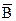 ; ;
|
| AìüU | º А; | Aîþ (AìüB) | º А; |
Aîþ 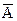
| º U; | Aìü (AîþB) | º А |
Равносильности теории множеств
| А½В | º Аìü 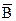 ; ;
| A½(В½С) | º (А½В)îþ(AìüС); |
| А½А | º Æ; | (A½В)½С | º A½BîþС; |
| А½ (ВîþС) | º (А½В)ìü(A½С); | A D В | º B D A; |
| А½ (ВìüС) | º (А½В)îþ(A½С); | A D В | º АîþВ ½ АìüВ; |
| (АìüВ)½С | º (А½С)ìü(В½С); | A D В | º (А½В)îþ (В½А); |
| (АîþВ)½С | º (А½С)îþ(В½С); | A D (ВD C) | º (A D В)D C; |
| А½(А½В) | º AìüB; | Аìü(В D C) | º (АìüВ) D (AìüC). |
4. Докажите тождества:
0)X ∪ 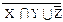 º Z ∪ X º Z ∪ X
 º º  ∩ ∩ 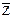 X ∩
X ∩  ∪ Z | ∪ Z |  º Z | º Z |  Y | (
Y | (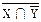 ∪ Z) º Æ; ∪ Z) º Æ;
| 1) X ∩Y∩(X∩Z∪X∩Y∩Z ∪Z∩ t) º X ∩Y∩Z
 º Y ∪ º Y ∪  ∪ ∪ 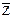 (X | (X |
(X | (X |  )) ∪ ( )) ∪ ( | ( | ( | |  )) º )) º 
 ∩ ( ∩ (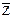 | X ∪ | X ∪ 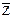 ) º Æ; ) º Æ;
|
2)  ∩Y∩ Z∪X∩Z º (X ∪Y) ∩Z
X∪ ∩Y∩ Z∪X∩Z º (X ∪Y) ∩Z
X∪  ∪ ∪ 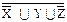 ºX∪Z∪ ºX∪Z∪  Y | (Y | X ∪
Y | (Y | X ∪  ) º Y ∩ X
( ) º Y ∩ X
(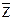 ∩ ∩  | X) | | X) | 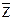 º Æ; º Æ;
| 3) X ∩Y∪X∩Y∩Z ∪X∩Y∩Z∪X∩Y∩Z º X∩Y
 º X ∩ º X ∩ 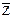 ∩ Y
(X | ∩ Y
(X |  ) | ) |  º X
(X ∩ º X
(X ∩  ) | ( ) | ( ∪ ∪  ) º Æ; ) º Æ;
|
4)  ∪ Y ∩ Z ∪ ∪ Y ∩ Z ∪  ∪ ∪  ∪ ∪ 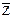 º U º U
 ∩ ∩  º º  ∩ ∩ 
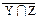 | | 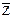 º Z | Y º Z | Y
 º Æ; º Æ;
| 5) ((X ∪ Y) ∪ ( ∩ ∩  )) ∩ )) ∩ 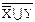 º X ∩ º X ∩ 
 º ( º ( ∪ Z) ∩ ∪ Z) ∩  X | Y ∪ X ∩ Z º X | Y ∩
X | Y ∪ X ∩ Z º X | Y ∩ 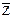
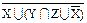 º Æ; º Æ;
|
6) 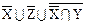 º U º U
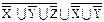 º X ∩ Y º X ∩ Y
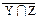 | |  º X ∩ º X ∩ 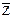 ∩ Y ∩ Y
 ∩ (Y ∪ Z) ∩ X ∩Y º Æ; ∩ (Y ∪ Z) ∩ X ∩Y º Æ;
| 7) (X ∪ Y ∪ Z) ∩ (X ∪ Y) ∪ Z º X ∪ Z ∪ Y
 º º  ∪ ∪  Y | (X ∩Y |
Y | (X ∩Y |  ) º Y | X ) º Y | X
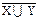 | |  ∪Y º Æ; ∪Y º Æ;
|
8) X ∪  ∪ X ∩ Z º U ∪ X ∩ Z º U
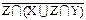 ∪ ∪  º º  ∪ ∪ 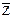 X ∪
X ∪ 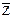 ∩ (Y| ∩ (Y|  ) º X ) º X
 | |  ∪ ∪ 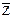 º Æ; º Æ;
| 9) (X ∪ Z) ∩ (X ∪ Y) ∩ (Y ∩ Z) º Y ∩ Z
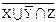 ∩ ∩ 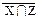 º (Y ∪ º (Y ∪ 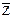 ) ∩ ) ∩  (
(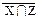 | | 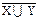 ) | ) |  º X | Z º X | Z
 ∩ ∩  º Æ; º Æ;
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1063; Нарушение авторских прав?; Мы поможем в написании вашей работы!