Ранг матрицы. Говорят, что ранг rankA матрицы A размера m×n равен r, если существует хотя бы одна несингулярная подматрица r-го порядка

Системы уравнений

Линейная алгебра

Говорят, что ранг rank A матрицы A размера m × n равен r, если существует хотя бы одна несингулярная подматрица r -го порядка, тогда как любая подматрица более высокого порядка является сингулярной.

Если это определение озвучить в терминах определителей, то оно будет выглядеть примерно так:

Матрица A размера m × n имеет ранг r, если существует хотя бы один отличный от нуля определитель r -го порядка, тогда как определитель любой подматрицы более высокого порядка равен нулю.

Очевидно, что rank A < min{ m,n }.

Для вычисления ранга матрицы можно использовать метод элементарных преобразований строк и столбцов – в точности тот самый метод, который применяется для вычисления определителей. Будет уместным напомнить основные операции метода:

1. Перестановка строк или столбцов.
2. Умножение строки или столбца на ненулевое число.
3. Прибавление к строке (столбцу) другой строки (столбца), предварительно умноженной на любое число.
4. Нулевая строка или столбец вычеркивается.

Целью элементарных преобразований является приведение матрицы к ступенчатой форме, т.е. к квазитреугольному виду - типа того, что представлено ниже:

.

(1)

Очевидно, что определитель третьего порядка, составленный из элементов первых трех строк и столбцов, отличен от нуля, и ранг матрицы равен 3:

Отметим, что любая матрица может быть представлена посредством эквивалентных преобразований (в смысле неизменности ее ранга) к блочному виду

(2)

где E - единичная матрица.

Например, для преобразования матрицы (1) к такому виду достаточно прибавить ко второму, третьему и пятому столбцам первый столбец с соответствующим образом подобранными коээффициентами, что приведет нас к матрице

Фактически, результаты этих преобразований чрезвычайно просты: во всех позициях первой строки - кроме первой - элементы превратились в нулевые.

Прибавляя затем второй столбец к третьему, четвертому и пятому - с соответствующим образом подобранными коээффициентами, получим

Далее поделим каждую строку на соответствующий коэффициент и удалим нулевые столбцы:

.

(3)

Рассматриваемая матрица приведена к вышеуказанному виду.

Пример.

Найти ранг матрицы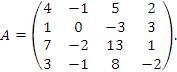

Решение. Непосредственным вычислением проверяется, что det A = 0. Следовательно, rank A < 4.

Однако существует минор третьего порядка, отличный от нуля. Таким минором является, например, определитель, составленный из элементов первой, второй, третьей строк и второго, третьего, четвертого столбцов.

Следовательно, rank A = 3.

Дата добавления: 2014-12-16