
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однородные системы линейных уравнений
|
|
|
|
Однородная система линейных уравнений имеет вид
 , ,
| (1) |
где A – матрица коэффициентов; X – матрица-столбец, составленная из неизвестных.
Очевидно, что любая однородная система имеет нулевое решение 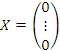 , которое называется тривиальным решением.
, которое называется тривиальным решением.
Теорема. Если 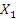 и
и 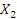 являются решениями однородной системы (1), то и их линейная комбинация
являются решениями однородной системы (1), то и их линейная комбинация
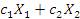
является решением этой системы.
Доказательство. По условию теоремы AХ 1=0 и AХ 2=0.
Тогда для любых чисел С 1 и С 2: С 1 AХ 1=0 Þ AС 1 Х 1=0 и С 2 AХ 2=0Þ AС 2 Х 2=0. Складывая эти выражения, получаем A (С 1 Х 1+ С 2 Х 2)= AС 1 Х 1+ AС 2 Х 2= С 1 AХ 1+ С 2 AХ 2=0. Следовательно, линейная комбинация С 1 Х 1+ С 2 Х 2 решений однородной системы линейных уравнений также является решением этой системы.
Примеры:
1. Решить систему уравнений
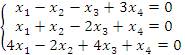 методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
методом Гаусса. Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
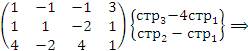  Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например,
Ранг матрицы равен 3, тогда как число неизвестных равно 4. Поэтому одну из неизвестных, например, 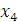 следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение следует рассматривать как свободный параметр. Далее нужно присвоить этому параметру произвольное значение 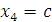 и выразить базисные неизвестные и выразить базисные неизвестные 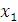 , , 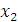 и и 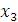 через c. Преобразованная матрица соответствует следующей системе уравнений: через c. Преобразованная матрица соответствует следующей системе уравнений:
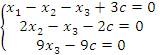 Из последнего уравнения следует, что
Из последнего уравнения следует, что  . Выразим остальные базисные переменные: . Выразим остальные базисные переменные:
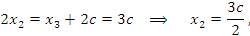 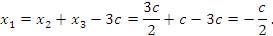 Таким образом, общее решение системы найдено:
Таким образом, общее решение системы найдено:
 Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
Чтобы найти частное решение, нужно придать параметру c какое-нибудь числовое значение. Полагая c = 4, получаем
 Проверка: Подставим неизвестные
Проверка: Подставим неизвестные
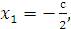 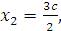  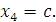 в уравнения системы:
в уравнения системы:
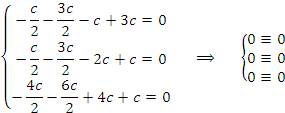 Уравнения обратились в тождества.
Уравнения обратились в тождества.
|
***
2. Пусть 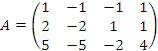 .
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду: .
Найти общее решение однородной системы линейных уравнений AX = 0. Решение. Преобразуем коэффициентную матрицу к ступенчатому виду:
 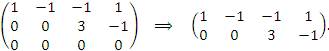 Поскольку
Поскольку  , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая 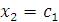 и и 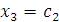 , получаем уклрлченную систему уравнений , получаем уклрлченную систему уравнений
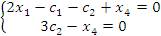 решение которой имеет вид
решение которой имеет вид
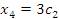 , , 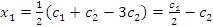 .
Запишем общее решение .
Запишем общее решение
 и представим его в виде линейной комбинации частных решений:
и представим его в виде линейной комбинации частных решений:
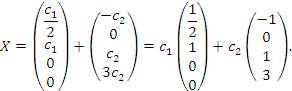 Если общее решение однородной системы представлено в виде линейной комбинации типа
Если общее решение однородной системы представлено в виде линейной комбинации типа
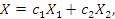 то говорят, что частные решения
то говорят, что частные решения  образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения образуют фундаментальную систему решений.
В рассматриваемом случае фундаментальную систему решений образуют частные решения 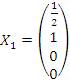 и и 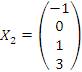 . .
|
***
3. Предположим, что общее решение однородной системы уравнений имеет вид
 Очевидно, что
Очевидно, что
 и поэтому частные решения
и поэтому частные решения
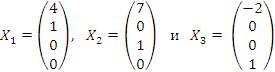 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
|
***
4. Дана матрица  . Решить однородную систему линейных уравнений AX = 0.
Решение. Преобразуем коэффициентную матрицу к треугольному виду: . Решить однородную систему линейных уравнений AX = 0.
Решение. Преобразуем коэффициентную матрицу к треугольному виду:
  Соответствующая система
Соответствующая система
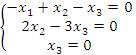 имеет только тривиальное решение
имеет только тривиальное решение 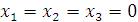 . .
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!