
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщенное правило Крамера
|
|
|
|
Теорема. Необходимым и достаточным условием совместности системы m линейных уравнений с n неизвестными
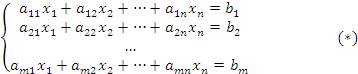
| (1) |
является равенство между собой рангов коэффициентной A и расширенной 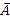 матриц.
матриц.
В русско-язычной литературе на эту теорему ссылаются как на теорему Кронекера-Капелли.
Следствия.
- Если rank à =rank A и совпадает с числом n неизвестных, то система (1) имеет единственное решение.
Это утверждение по сути представляет собой просто другую формулировку правила Крамера
- Если rank à =rank A>n, то система (1) имеет бесконечное множество решений.
Схема:
Равенство рангов коэффициентной и расширенной матриц означает совместность системы уравнений (1). При этом число r=rank à =rank A устанавливает количество базисных переменных, тогда как остальные (n - r) переменные играют роль свободных параметров и могут принимать любые значения. Каждому набору параметров, число которых бесконечно велико, соответствует свое решение.
Примеры:
1. Докажем необходимость условия, сформулированного в теореме, т.е. покажем, что предположение о совместности системы уравнений влечет за собой равенство рангов, 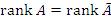 .
.
Рассмотрим расширенную матрицу

и преобразуем ее, выполнив элементарные операции над столбцами.
Вычтем из последнего столбца первый столбец, умноженный на 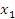 , второй столбец умноженный на
, второй столбец умноженный на 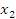 , и т.д. При этом ранг матрицы не меняется:
, и т.д. При этом ранг матрицы не меняется:
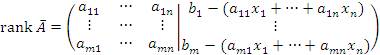
С учетом уравнений (1), последний столбец является нулевым и поэтому его можно опустить. Тогда
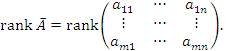
2. Перейдем к доказательству достаточности условия.
Покажем, что равенство рангов r=rank à =rank A влечет за собой совместность системы (1).
Если r= rank A, то существует несингулярная подматрица Ã r -го порядка. Ее матричные элементы (коэффициенты при неизвестных) указывают – какие именно r уравнений "образуют базис" данной системы уравнений - в том смысле, что каждое из оставшихся уравнений является следствием "базисных" уравнений (их линейной комбинацией).
Поэтому можно перейти к укороченной системе r уравнений и выбрать r неизвестных в качестве базисных переменных. Остальные (n - r) переменные будут при этом выступать в качестве свободных параметров, которым можно придавать произвольные числовые значения.
Укороченная система r линейных уравнений полностью эквивалентна исходной системе и имеет (согласно теореме Крамера) единственное решение для любого набора значений свободных параметров.
Примеры:
1. Дана система линейных уравнений,
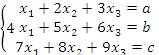 Установить соотношения между параметрами a, b и c, при которых система является несовместной. Решение. Составим расширенную матрицу и преобразуем ее к ступенчатой форме:
Установить соотношения между параметрами a, b и c, при которых система является несовместной. Решение. Составим расширенную матрицу и преобразуем ее к ступенчатой форме:
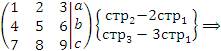 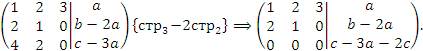 Если
Если 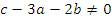 , то система является несовместной. В противном случае одна из неизвестных является свободной переменной и, следовательно, система имеет бесконечное множество решений. , то система является несовместной. В противном случае одна из неизвестных является свободной переменной и, следовательно, система имеет бесконечное множество решений.
|
***
2. Система линейных уравнений задана расширенной матрицей, представленной в приведенно-ступенчатой форме:
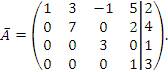 Выяснить сколько решений имеет эта система. Решение. Очевидно, что ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы и совпадает с числом неизвестных. Следовательно, система уравнений имеет единственное решение – согласно следствию из обобщенного правила Крамера.
Выяснить сколько решений имеет эта система. Решение. Очевидно, что ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы и совпадает с числом неизвестных. Следовательно, система уравнений имеет единственное решение – согласно следствию из обобщенного правила Крамера.
|
***
3. Выяснить сколько решений имеет система линейных уравнений, заданная расширенной матрицей
 при различных значениях параметра a. Решение. Если
при различных значениях параметра a. Решение. Если 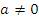 , то , то 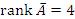 , тогда как , тогда как 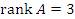 . В этом случае система является несовместной и не имеет решений.
Если a = 0, то . В этом случае система является несовместной и не имеет решений.
Если a = 0, то 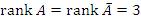 , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.
Следовательно, система имеет бесконечное множество решений. , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.
Следовательно, система имеет бесконечное множество решений.
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 572; Нарушение авторских прав?; Мы поможем в написании вашей работы!