Эпюра продольных сил. Напряжения

Центральным растяжением (сжатием) называется такой вид деформации, при котором в попереч­ных сечениях бруса (стержня) возникает только продольная (нормальная) сила. Считается, что внутрен­няя продольная сила действует вдоль оси стержня, перпендикулярно к его поперечным сечениям. Чис­ленные значения продольных сил N определяют по участкам, используя метод сечений, составляя урав­нения равновесия суммы проекций на ось бруса (z) всех сил, действующих на отсечённую часть.

Растягивающие продольные силы принято считать положительными, а сжимающие - отрицатель­ными.

Рассмотрим (рис. 1.2, а) прямой брус постоянной толщины, закреплённый одним концом и нагру­женный на другом конце силой Р, направленной вдоль его оси. Под действием закрепления и внешней силы Р брус растягивается (деформируется). При этом в закреплении возникает некоторое усилие, бла­годаря которому верхний край брусаостаётсянеподвижным. Это усилие называют реакцией закрепле­ния на внешнюю нагрузку. Заменим влияние закрепления на стержень эквивалентно действующей си­лой. Эта сила равна реакции закрепления R (рис. 1.2, б).

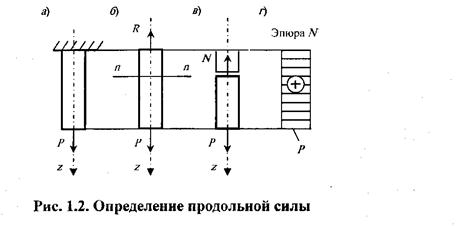
Под действием двух внешних воздействий: известной силы Р и неизвестной пока реакции R- брус находится в равновесии. Уравнение равновесия бруса

При построении уравнений общего равновесия механики принято следующее правило знаков: про­екция усилия на ось положительна, если её направление совпадает с выбранным направлением этой оси, проекция отрицательна, если направлена в противоположную сторону.

Мысленно разрежем стержень на две части по интересующему нас сечению п-п (рис. 1.2, б). Влияние на нижнюю часть верхней части представим действием на нижнюю часть в её верхнем торце n-п нор­мальной силы N (рис. 1.2, в). Уравнение равновесия нижней отсечённой части бруса:

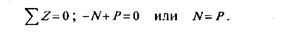
График изменения продольной силы вдоль оси бруса показан на рис. 1.2, г. График, показывающий изменение продольных сил по длине оси бруса, называется эпюрой продольных сил (эпюрой N ).

Пример. Построить эпюру внутренних нормальных сил, возникающих под действием трёх внеш­них сил (см. рис. 1.3): Р₁=5 кН, P₂ = 8 кН, Р₃, = 7 кН (см. рис. 1.3, а).

Используя метод сечений, определим значения внутренней силы в характерных поперечных сече­ниях бруса.

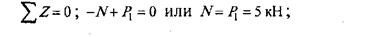
Уравнение равновесия нижней отсчетной части бруса:

сечение II-II

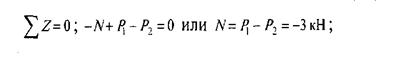
cечение I-I

сечение III-III

ƩZ= 0; -N+ Р₁- Р₂ + Р₃=0 или N=Р₁-Р₂ + Р₃ =4 кН.

Строим эпюру нормальных сил (см. рис. 1.3,б)

Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодейст­вующую внутренних нормальных сил, распределённых по площади поперечного сечения, и связана с возникающими в этом сечении нормальными напряжениями зависимостью

N= dF

Под действием двух внешних воздействий: известной силы Р и неизвестной пока реакции R- брус находится в равновесии. Уравнение равновесия бруса

или

При построении уравнений общего равновесия механики принято следующее правило знаков: проекция усилия на ось положительна, если её направление совпадает с выбранным направлением этой оси, проекция отрицательна, если направлена в противоположную сторону.

Мысленно разрежем стержень на две части по интересующему нас сечению п-п (рис. 1.2, б). Влияние на нижнюю часть верхней части представим действием на нижнюю часть в её верхнем торце п-п нормальной силы N (рис. 1.2, в). Уравнение равновесия нижней отсечённой части бруса

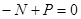или

Продольная сила N, возникающая в поперечном сечении бруса, представляет собой равнодействующую внутренних нормальных сил, распределённых по площади поперечного сечения, и связана с возникающими в этом сечении нормальными напряжениями зависимостью

здесь σ - нормальное напряжение в произвольной точке поперечного сечения, принадлежащей элемен­тарной площадке dF; F- площадь поперечного сечения бруса.

Произведение σdF=dN представляет собой элементарную внутреннюю силу, приходящуюся на площадку dF.

Значение продольной силы N в каждом частном случае легко можно определить при помощи мето­да сечений. Для нахождения напряжений в каждой точке поперечного сечения бруса надо знать закон их распределения по этому сечению.

Проведём на боковой поверхности бруса до его нагружения линии, перпендикулярные к оси бруса (рис. 1.4, а).

Каждую такую линию можно рассматривать как след плоскости поперечного сечения бруса. При нагружении бруса осевой силой Р эти линии, как показывает опыт, остаются прямыми и параллельными между собой (их положения после нагружения бруса показаны на рис. 1.4, б).

Это позволяет считать, что поперечные сечения бруса, плоские до его

на­гружения, остаются плоскими и при действии нагрузки. Такой опыт

Рис. 1.4. Деформирование бруса

подтвер­ждает гипотезу плоских сечений (гипотезу Бернулли).

Согласно гипотезе плоских сечений, все продольные волокна бруса растяги­ваются одинаково, значит их растягивают одинаковые по величине силы о dF = dN, следовательно, во всех точках поперечного сечения нормальное на­пряжение о имеет постоянное значение.

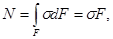
откуда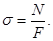

В поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределённые нормальные напряжения, равные от­ношению продольной силы к площади поперечного сечения.

Для наглядного изображения изменения нормальных напряжений в поперечных сечениях стержня (по его длине) строится эпюра нормальных напряжений. Осью этой эпюры является отрезок прямой, равный длине стержня и параллельный его оси. При стержне постоянного сечения эпюра нормальных напряжений имеет такой же вид, как и эпюра продольных сил (она отличается от неё лишь принятым масштабом). При стержне же переменного сечения вид этих двух эпюр различен; в частности, для стержня со ступенчатым законом изменения поперечных сечений эпюра нормальных напряжений имеет скачки не только в сечениях, в которых приложены сосредоточенные осевые нагрузки (где имеет скачки эпюра продольных сил), но и в местах изменения размеров поперечных сечений.

Дата добавления: 2014-12-16