Кручение бруса с круглым поперечным сечением

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и по­перечные силы) равны нулю.

Для крутящего момента, независимо от формы сечения, принято следующее правило знаков. Если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит момент М _K направ­ленным против часовой стрелки, то момент считается положительным. При противоположном направ­лении моменту приписывается знак минус.

Рассмотрим стержень, нагруженный по концам моментами М (рис. 1.8). Если посмотреть на одну его плоскость со стороны внешней нормали, то мы увидим, что момент M _K направлен по часовой стрелке. Следовательно, М _K будет отрицательным. Тот же самый результат может быть получен, если посмот­реть из точки со стороны внешней нормали на другую его плоскость.

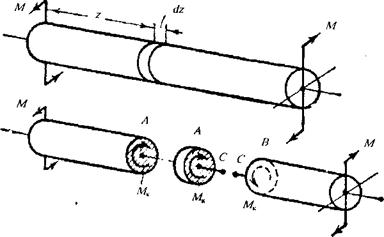
Рис. 1.8. Брус, нагруженный моментами.

При расчёте стержня на кручение надо решить две основные задачи. Требуется определить напря­жения и найти угловые перемещения в зависимости от внешних моментов. Эти задачи решаются по- разному, смотря по тому, какой вид имеет поперечное сечение стержня. Наиболее просто можно полу­чить решение в случае кругового сечения, а также для широкого класса тонкостенных стержней.

Указанным правилом руководствуются при построении эпюр крутящих моментов (рис. 1.9).

Механизм деформирования стержня с круглым поперечным сечением можно представить себе в следующем виде: будем считать, что каждое поперечное сечение в результате действия внешних мо­ментов поворачивается в своей плоскости на некоторый угол как жёсткое целое. Этот угол поворота для различных сечений будет различным. Сказанное представляет собой гипотезу плоских сечений - пред­положение, оправдываемое общими правдоподобными соображениями о характере возникающих пере­мещений.

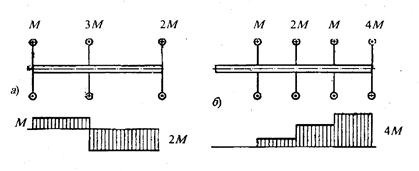
Рис. 1.9. Эпюры крутящих моментов.

Окончательным критерием пригодности любой гипотезы является опыт. Получив расчётную фор­мулу, нужно, прежде всего, сопоставить результаты расчёта с экспериментом, и если между ними обна­руживается достаточно хорошее соответствие, гипотеза считается приемлемой.

В данном случае принятая гипотеза носит название гипотезы плоских сечений.

В поперечных сечениях стержня возникает постоянный крутящий момент

Двумя поперечными сечениями выделим из стержня элемент длиной dz, а из него в свою очередь двумя цилиндрическими поверхностями с радиусами ρ и ρ + dρ выделим элементарное кольцо.

Правое торцевое сечение кольца поворачивается при кручении относительно левого на угол dφ. Об­разующая цилиндра АВ поворачивается при этом на угол γ и занимает положение АВ^'. Отрезок ВВ^' ра­вен, с одной стороны, ρdφ, а с другой - γdz. Следовательно,

.

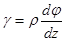Угол γ представляет собой не что иное, как угол сдвига цилиндрической поверхности. Величина dφ/dz обозначается обычно через θ,

,

и называется относительным углом закручивания. Это — угол взаимного поворота двух сечений, отнесён­ный к расстоянию между ними. Величина θ аналогична относительному удлинению при растяжении ∆l1. Вводя обозначение θ, получим

По закону Гука для сдига

,

где τ — касательные напряжения, возникающие в поперечном сечении бруса. Парные им напряжения воз­никают в продольных плоскостях - в осевых сечениях.

Элементарные силы τdF приводятся к крутящему моменту

Интегрирование распространяется на всю площадь поперечного сечения F. Подставляя в подынте­гральную функцию напряжение τ из последней формулы, получим

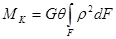
Записанный в формуле интеграл представляет собой чисто геометрическую характеристику(см. п. 2), измеряется в см⁴ и носит название полярного момента инерции сечения:

Таким образом, получаем 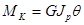, или

.

Произведение GJ_p называют жесткостью стержня при кручении.

Через относительный угол закручивания θ легко определяется и величина взаимного угла поворота сечений φ. Имеем

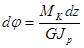
откуда

,

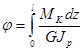где l - расстояние между сечениями, для которых определяется взаимный угол поворота φ.

Если крутящий момент по длине стержня не изменяется, М_к = М, и если жёсткость остаётся посто­янной, то

.

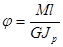Проведя преобразования, получим

.

Таким образом, касательные напряжения в поперечном сечении распределены вдоль радиуса по ли­нейному закону и имеют наибольшее значение в точках, наиболее удалённых от оси. При этом

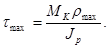
Величина 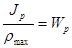называется полярным моментом сопротивления и измеряется в см³. Окончательно имеем

Эти формулы являются основными расчётными формулами для кручения стержня с круговым по­перечным сечением. Они справедливы как для сплошного, так и для полого кругового сечения.

Определим теперь величины геометрических характеристик сечения J_p и W_p. Если стержень имеет сплошное круговое сечение, то

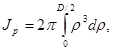
где D - диаметр сечения, или

Если же в стержне имеется внутренняя центральная полость диаметра d, то

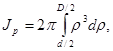
или

.

Соответственно этим выражениям определяем полярный момент сопротивления W_p:

для сплошного сечения

для кольцевого сечения (полый вал)

Таким образом, при заданном крутящем моменте угловые перемещения вала обратно пропорцио­нальны четвёртой степени диаметра. Что же касается наибольшего напряжения, то оно обратно пропор­ционально кубу диаметра D.

Касательные напряжения в поперечных сечениях бруса направлены в каждой точке перпендику­лярно к текущему радиусу р. Из условия парности следует, что точно такие же напряжения возникают и в продольных сечениях бруса. Наличие этих напряжений проявляется, например, при испытании на кручение деревянных образцов.

Дата добавления: 2014-12-16