Внутренние силовые факторы, возникающие в поперечных сечениях бруса при изгибе

ИЗГИБ.

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возни­кают изгибающие моменты. Если изгибающий момент в сечении является единственным силовым фак­тором, а поперечные и нормальная силы отсутствуют, изгиб называется чистым. Большей частью, одна­ко, в поперечных сечениях бруса наряду с изгибающими моментами возникают также и поперечные си­лы. В этом случае изгиб называют поперечным, Классификация видов изгиба производится и по другим признакам, некоторые из которых будут рассмотрены в дальнейшем. Брус, работающий в основном на изгиб, часто называют балкой.

Для того чтобы правильно ориентироваться в вопросах, связанных с расчётом бруса на изгиб, необ­ходимо, прежде всего, научиться определять законы изменения внутренних силовых факторов, т.е. нау­читься строить эпюры изгибающих моментов и поперечных сил. Рассмотрим некоторые характерные примеры и установим необходимые правила.

Простейшая двухопорная балка, нагруженная силой P показана на(рис. 1.15, а). Напомним ещё раз, что показанная система, как и все, которые рассматривались до сих пор и будут рассмотрены в даль­нейшем, получена как результат операций, связанных с выбором расчётной схемы. К анализу схемы двухопорной балки сводится расчёт очень многих машиностроительных конструкций, например балки мостового крана, показанной на (рис. 1.16).

Анализ внутренних сил начинается обычно с определения полной системы внешних сил. В данном случае необходимо определить реакции опор. Из условий равновесия определяем реакции:

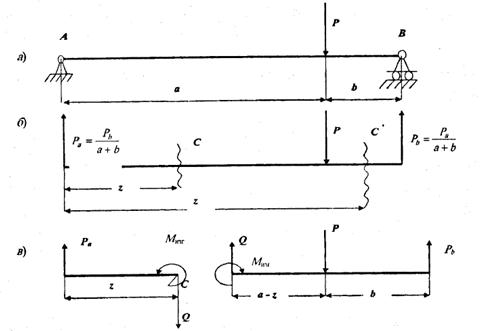
Рис. 1.15. Определение изгибающего момента

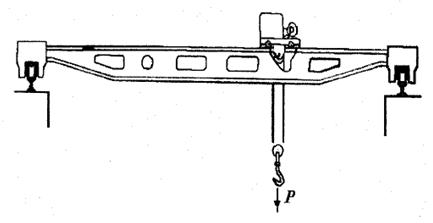
Рис. 1.16. Мостовой кран

На расстоянии z, от левой опоры проведём сечение С (рис. 1.15) и разделим балку мысленно на две части. Для того чтобы каждая из частей находилась в равновесии, в сечении С необходимо приложить силу Q и момент М. Эти силовые факторы определяются из условий равновесия одной из частей бруса. В - величина внутренних сил не зависит от того, рассматриваются ли условия равновесия правой пли левой части бруса (рис. 1.15, в). В данном случае удобнее рассматривать левую часть.

Если взять сумму моментов всех сил, действующих на левую часть бруса, относительно централь­ной поперечной оси в сечении С и приравнять эту сумму нулю, то получим

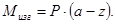
Если бы слева от сечения С действовала не одна, а несколько сил, величина изгибающего момента М_изг в сечении определилась бы суммой моментов этих сил. Таким образом, изгибающий момент в се­чении может рассматриваться как сумма моментов относительно поперечной оси сечения всех сил, рас­положенных по одну сторону от этого сечения. В дальнейшем, для того чтобы избежать громоздких ри­сунков, иллюстрирующих равновесие отсечённых частей бруса, изгибающий момент будем определять именно так.

Знак изгибающего момента устанавливается по знаку кривизны изогнутого бруса (рис. 1.17) и зави­сит от выбранного направления осей внешней неподвижной системы координат zy. Если ось у (рис. 1.17) направить в обратную сторону, то знак кривизны, а следовательно, и момента изменится на обрат­ный. Этим правилом знаков пользуются при определении перемещений бруса и при определении фор­мы изогнутой оси. При построении эпюр изгибающих моментов используется другое правило знаков (правило относительных знаков), при котором знак момента не зависит от направления внешних осей. Эпюра моментов строится на оси бруса, и ордината момента откладывается в сторону вогнутости упру­гой линии, т.е., как говорят, эпюра моментов строится на сжатом волокне. Этому правилу можно дать и другое толкование. Если сумма моментов сил, действующих на левую часть бруса, даёт равнодейст­вующий момент, направленный по часовой стрелке, то ордината изгибающего момента в сечении от­кладывается вверх. Если же равнодействующий внешний момент слева от сечения направлен против часовой стрелки, ордината изгибающего момента откладывается вниз.

Рис 1.17.Знаки изгибающего момента Рис 1.18.Ориентация изгибающего момента

Для сил, лежащих справа от сечения, имеет место обратная зависимость: в случае равнодействую­щего момента, направленного по часовой стрелке, - вниз, а в случае равнодействующего момента, направленного против часовой стрелки, - вверх. Сказанное иллюстрируется схемой, представленной на (рис. 1.18).

Возвращаясь к рассматриваемому примеру двухопорной балки, замечаем, что момент силы Р_a, рас­положенной слева от сечения С, направлен по часовой стрелке. Следовательно, в сечении С ордината изгибающего момента откладывается вверх.

В пределах изменения z от 0 до а изгибающий момент равен

Для правого участка вменяется в пределах от а до {а+ Ь). Изгибающий момент в сечении Судобнее рассматривать как сумму моментов внешних сил, лежащих справа от сечении. Очевидно,

Ордината момента отложена вверх, так как момент внешней силы, лежащей справа от сечения С, направлен против часовой стрелки. В соответствии с полученными выражениями для изгибающих мо­ментов может быть построена эпюра, показанная на рис. 1.19. Эпюра является кусочно линейной и на всей длине балки расположена сверху. Это значит, что ось изогнутой балки, называемая упругой лини­ей, всюду направлена вогнутой стороной вверх, что в данном случае достаточно очевидно.

Рис. 1.19. Построение эпюр.

Определим поперечные силы Q. Из условия равновесия левой или правой части разрезанного бруса (рис.1.15) следует, что

Q=P_a, или Q= Р - Р_а= Р_b.

Во всех случаях поперечная сила для прямого бруса равна сумме проекций на плоскость сечения всех внешних сил, лежащих по одну сторону от сечения. Отсюда устанавливается правило знаков для поперечной силы. Если сумма внешних сил, лежащих по левую сторону от сечения, даёт равнодейст­вующую, направленную вверх, то поперечная сила в сечении считается положительной, вниз — отрица­тельной. Справа вниз — знак «плюс», справа вверх — знак «минус». Это правило иллюстрируется схемой, показанной на (рис. 1.20).

В рассматриваемом случае двухопорной балки сила Р _a, лежащая слева от сечения С, направлена вверх. Следовательно,

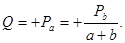
Для правого участка балки сила Рь расположенная справа от сечения С, направлена вверх. Следова­тельно, на этом участке поперечная сила будет отрицательной:

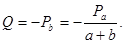
Эпюра поперечных сил в рассматриваемой двухопорной балке изобразится двумя прямоугольника­ми (рис. 1.19).

Рассмотрим ещё несколько примеров построения эпюр изгибающих моментов и поперечных сил.

Двухопорная балка длиной l нагружена равномерно распределёнными силами собственного веса. Эти силы характеризуются интенсивностью нагрузки q Н/м, т.е. силой, приходящейся на единицу длины бру­са (рис. 1.21). Определяем реакции опор. Очевидно,

Обычно, для упрощения прибегают к условному изображению реакций.

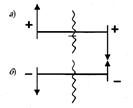
Рис. 1.20. Знаки поперечных сил.

Рис. 1.21. Построение эпюр.

Сумма моментов внешних сил, лежащих по одну сторону от сечения, например по левую, равна

где P_az - момент силы Р_а направлен по часовой стрелке (знак плюс);

qz - сила собственного веса на длине z её равнодействующая проходит через середину отрезка z. Следовательно, плечо силы равно z/2, а момент этой силы, расположенной слева от сечения С, направлен против часовой стрелки (знак «минус»). Таким образом,

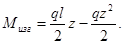
Эпюра изгибающего момента изображается параболой, показанной на (рис. 1.21). Наибольшее значе­ние изгибающий момент имеет в среднем сечении пролета при z= 2;

Поперечная сила в сечении С равна сумме сил, лежащих по одну сторону от сечения:

Эпюра поперечной силы изображается прямой.

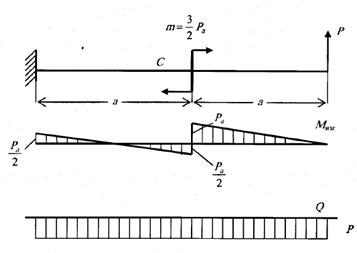
Рис. 1.22. Изгиб балки.

Построение эпюр изгибающих моментов и поперечных сил на примере балки защемлённой одним концом показано на (рис. 1.22).

Такого рода балки называются обычно консолями. В данном случае с правой стороны на балку не наложено связей и определение изгибающих моментов и поперечных сил в любом сечении может быть произведено без предварительного определения реакций.

В среднем сечении консоли к балке через крестовину передаётся момент пары сил. В результате на эпюре изгибающих моментов возникает скачок. При переходе через сечение С сумма моментов сил, рас­положенных по правую или левую сторону от сечения, меняется сразу на величину М. Рассматривая все построенные выше эпюры, нетрудно подметить определённую закономерную связь между эпюрами из­гибающих моментов и эпюрами поперечных сил.

Судя по виду эпюр, поперечная сила Q представляет собой производную от изгибающего момента М по длине бруса. Докажем, что эта закономерность действительно имеет место.

Пусть брус закреплён произвольным образом и нагружен в общем случае распределённой нагруз­кой интенсивности q= f(z) Принятое направление для q будем считать положительным (рис. 1.23).

Выделим из бруса элемент длиной dz и в произведённых сечениях приложим моменты М и М + dM, а также поперечные силы Q и Q + dQ. Направления дли этих силовых факторов приняты положитель­ными в соответствии с обусловленным выше правилом знаков. В пределах малого отрезка dz нагрузку q можно считать распределённой равномерно.

Рис. 1.23. Построение эпюр.

Приравниваем нулю сумму проекций всех сил на вертикальную ось и сумму моментов относитель­но поперечной оси С (рис. 1.23)

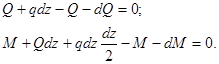
Производя упрощения и отбрасывая величину высшего порядка малости, получим

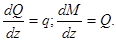
Таким образом, поперечная сила действительно представляет собой производную от изгибающего момента по длине бруса. Производная же от поперечной силы даёт интенсивность внешней распреде­лённой нагрузки q.

Из соотношений можно сделать некоторые общие выводы о характере эпюр изгибающих моментов и поперечных сил для прямого бруса.

Если брус нагружен равномерно распределённой нагрузкой интенсивности q = const, очевидно, функция Q будет линейной, а М- квадратичной.

Если брус нагружен сосредоточенными силами или моментами, то в промежутках между точками их приложения интенсивность q = 0. Следовательно, Q = const, а М является линейной функцией z В точках приложения сосредоточенных сил эпюра Q претерпевает скачок на величину внешней силы, а в эпюре М возникает соответствующий излом (разрыв в производной).

Дата добавления: 2014-12-16