Внутренние силовые факторы, возникающие в поперечных сечениях бруса при изгибе

Вопросы для повторения и закрепления материала

Цели и задачи изучения темы

{Определите цели и задачи изучения темы.}

Результат освоения темы:

Индекс компетенции	Индекс образовательного результата	Образовательный результат

2.1. {название первого параграфа темы}

{Введите название первого параграфа темы и текст параграфа. }

2.1.1. {название первого вопроса первого параграфа темы}

{Введите название первого вопроса первого параграфа темы и текст вопроса. }

2.1.2. {название второго вопроса первого параграфа темы}

{Введите название второго вопроса первого параграфа темы и текст вопроса. }

2.2. {название второго параграфа темы}

{Введите название первого параграфа темы и текст параграфа. }

2.2.1. {название первого вопроса второго параграфа темы}

{Введите название первого вопроса второго параграфа темы и текст вопроса. }

2.2.2. {название первого вопроса второго параграфа темы}

{Введите название второго вопроса второго параграфа темы и текст вопроса. }

{Введите вопросы для повторения и усвоения материала по теме.}

1……

2……

3……

Задания для самостоятельной работы

Рассмотрим балку, на которую действует пара сил с моментом т и внешняя сила F (рис. 29.3а). Для определения вну­тренних силовых факторов пользуемся методом сечений. Рассмотрим равновесие участка 1 (рис. 29.36). Под действием внешней пары сил участок стремится развер­нуться по часовой стрелке. Силы упругости, возникающие в сече­нии 1, удерживают участок в равновесии. Продольные силы упругости выше оси бруса направлены направо, а силы ниже оси направлены налево. Испытание стальных образцов на продольный изгиб Цель работы –демонстрация явления потери устойчивости формы стержней; определение величин критических сил при продольном изгибе стержней различных размеров с разным способом закрепления концов и сопоставление установленных в опыте величин критических сил с их значениями, рассчитанными по соответствующим формулам сопротивления материалов. Таким образом, при равновесии участка 1 получим: ΣFz = 0. Продольная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси Ох:

Этот момент называют изгибающим моментом Мх = Ми.

Из схемы вала на рис. 29.36 видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения а равны нулю.

Такой слой называют нейтральным слоем (НС). Линия пересе­чения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.

Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.

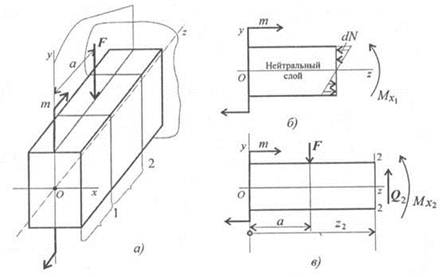
Рис. 29.3

Практически величина изгибающего момента в сечении опреде­ляется из уравнения равновесия: ; .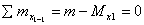

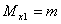Таким образом, в сечении 1-1 продольная сила равна нулю, из­гибающий момент в сечении постоянен.

Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом.

Рассмотрим равновесие участка бруса от свободного конца до сечения 2

(рис. 29.Зв).

Запишем уравнения равновесия для участка бруса:

; ; .

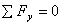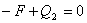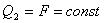В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.

; .

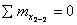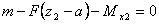Изгибающий момент в сечении: МХ2 = т - F(z2 - а);

z2 — расстояние от сечения 2 до начала координат.

Изгибающий момент зависит от расстояния сечения до начала координат.

Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.

Решение первой задачи сводится к определению необходимого числа функций времени (уравнений движения), однозначно определяющих положение каждой точки тела в пространстве. Решение второй задачи заключается в определении зависимостей, позволяющих по известным уравнениям движения определить траекторию, а также скорость и ускорение любой точки тела в любой момент времени.

Дата добавления: 2014-12-16