Поперечного сечения

Прежде всего, можно довольно просто установить, что касательные напряжения в поперечных сечениях для точек, расположенных вблизи контура, направлены по касательной к дуге контура. Действительно, по­ложим, что в какой-то точке касательное напряжение τ вблизи контура на­правлено под некоторым углом к контуру. Разложим это напряжение на две составляющие - по касательной к контуру и по нормали.

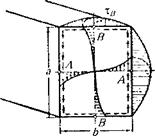
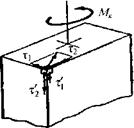
Рис. 1.11. Напряжения при кручении Рис. 1.12. Эпюра касательных напряжений

По условию парности на свободной поверхности стержня должно возникнуть касательное напряже­ние τ^'_n = τ_n. Но внешняя поверхность свободна от нагрузки и к ней никаких внешних сил не приложено, кроме, разве что, сил атмосферного давления. Таким образом, τ^'_n = 0. Следовательно, τ_n = 0, и касатель­ное напряжение τ вблизи контура направлено по касательной к контуру.

Совершенно аналогично можно показать, что в случае, если поперечное сечение имеет внешние уг­лы, то в них касательные напряжения обращаются в нуль (рис. 1.11). Раскладывая напряжение τ вблизи угла на две составляющие по нормалям к сторонам угла, получаем напряжения τ₁ и τ₂. Так как парные им напряжения τ^'₁ и τ^'₂ равны нулю, то в нуль обращаются и напряжения τ₁ и τ₂. Значит, вблизи внешне­го угла касательные напряжения в поперечном сечении отсутствуют.

Если рассмотреть полученную методами теории упругости эпюру касательных напряжений для бруса прямоугольного сечения (рис. 1.12), то как мы увидим, напряжения равны нулю, а наибольшие напряжения возникают по серединам больших сторон: в точке А:

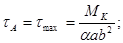
в точке B:

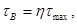
где а - большая, b - малая стороны прямоугольника.

Коэффициенты а и η зависят от отношения сторон a/b. Значения этих коэффициентов задаются втаблице.

Угловое перемещение

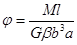
Коэффициент β также является функцией отношения a/b.

Дата добавления: 2014-12-16