Чистый сдвиг и его особенности

СДВИГ И КРУЧЕНИЕ.

На примере растяжения и сжатия были выявлены некоторые наиболее важные свойства напряжён­ного состояния. При растяжении в зависимости от ориентации секущих площадок на гранях выделенно­го прямоугольного элемента возникают как нормальные, так и касательные напряжения. Последние, не­зависимо от величины нормальных напряжений, подчиняются условию парности.

Теперь положим, что имеется такое напряжённое состояние, когда на гранях выделенного элемента возникают только касательные напряжения. Такое напряжённое состояние называется чистым сдвигом (более строгое определение чистого сдвига будет дано позднее на основе общей теории напряжённого состояния).

В качестве примера, иллюстрирующего состояние однородного чистого сдвига, можно рассмотреть тонкостенную цилиндрическую трубку, нагруженную моментами, приложенными в торцовых плоско­стях.

Величина напряжения т определяется из условий равенства момента равномерно распределённых по поперечному сечению внутренних сил моменту:

где R - радиус трубки; δ - толщина трубки.

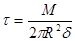
Рассмотрим деформации при сдвиге. Касательное напряжение τ связано с угловой деформацией γ соотношением:

,

Где

.

В результате возникающих угловых деформаций пластина перекашивается, а торцовые сечения труб­ки получают взаимные угловые смещения φ.

.

Аналогично испытанию на растяжение и сжатие можно провести испытание материала в условиях чистого сдвига. Для этого удобнее всего воспользоваться испытанием тонкостенной трубки. Сопостав­ление диаграммы сдвига с диаграммой растяжения для одного и того же материала показывает их каче­ственное сходство. На диаграмме сдвига также имеется упругая зона, зоны текучести и упрочнения.

Аналогичным образом для сдвига, как и для растяжения, можно было бы дополнительно ввести ха­рактеристики - предел пропорциональности при сдвиге, предел упругости, предел текучести и пр.

Прежде, когда изучение механики деформируемых тел находилось ещё в начальной стадии, так обычно и поступали. В дальнейшем, однако, было установлено, что характеристики сдвига связаны с характеристиками растяжения. В настоящее время теория пластичности даёт возможность построить теоретически диаграмму сдвига по диаграмме растяжения, а также выразить все характеристики сдвига через уже знакомые нам механические характеристики растяжения. Точно так же допускаемые напря­жения и коэффициенты запаса при чистом сдвиге могут быть связаны с соответствующими величинами для простого растяжения.

Напряжённое состояние, изображённое на рис. 1.7, а представляет собой чистый сдвиг. В этом со­стоянии длины ребер элементарного параллелепипеда не изменяются, а изменяются лишь углы между боковыми гранями: первоначально прямые углы становятся равными 90° + у и 90° - у (рис. 1.17, б).

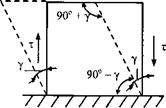
Рис. 1.7. Деформация при сдвиге.

Каждая из граней параллелепипеда при деформации чистого сдвига перемещается относительно противоположной грани на величину АА', называемую абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию между противоположными гранями называется относительным сдвигом, при ма­лых деформациях оно равно углу сдвига γ - изменения первоначально прямых углов между боковыми гранями параллелепипеда. Абсолютный сдвиг выражается в мерах длины, а относительный сдвиг явля­ется безразмерной величиной. Угол сдвига γ, как показывает опыт, прямо пропорционален касательным напряжениям. Эта зависимость между γ и τ, называемая законом Гука при сдвиге, выражается в виде

или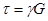

Она справедлива при напряжениях, не превышающих предела пропорциональности материала.

Коэффициент пропорциональности G в формулах называется модулем сдвига (или модулем упру­гости второго рода).

Модуль сдвига является физической постоянной материала, характеризующей его жёсткость (т.е. способность сопротивляться упругим деформациям) при сдвиге. Модуль сдвига G, как и модуль упру­гости Д выражается в паскалях (Па), мегапаскалях (МПа).

Дата добавления: 2014-12-16