Поняття вектора

СТАТИКА

Статика – це розділ теоретичної механіки, в якому викладається загальне вчення про сили і вивчаються умови рівноваги матеріальних тіл, що знаходяться під дією сил.

Під рівновагою тіла в статиці мається на увазі стан його спокою відносно інших тіл, що сприймаються як нерухомі.

Елементи векторної алгебри

У теоретичній механіці розглядаються такі векторні величини як сила, момент сили відносно точки та осі, момент пари сил, швидкість, прискорення та інші.

Для визначеності розглядаємо прямокутну декартову систему координат.

Вектор – це спрямований відрізок, який характеризується довжиною і напрямом.

Операції над векторами. Вектори можна складати і множити на число:

сума двох векторів є вектор;

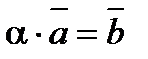множення вектора на дійсне число є вектор;

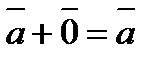існує нульовий вектор.

У математиці всі вектори є вільними, їх можна переносити паралельно самим собі.

Рисунок. 1.1

У сумі двох векторів (рис. 1.1а) початок другого вектора можна помістити у кінець першого вектора, тоді суму двох векторів можна представити як вектор, що має початок у початку першого вектора, а кінець в кінці другого вектора. Застосовуючи це правило для суми декількох векторів (рис. 1.1б),отримуємо, що сумою декількох векторів є вектор, що замикає ламану лінію, що складається з векторів доданків.

Операції над векторами підпорядковуються таким законам (див. рис. 1.2):

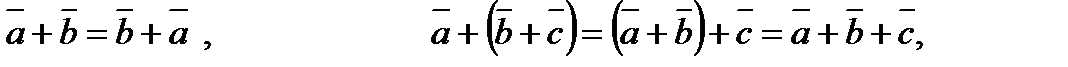
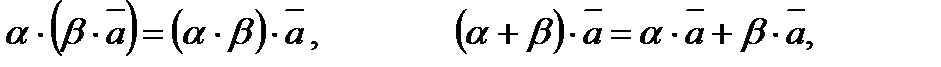
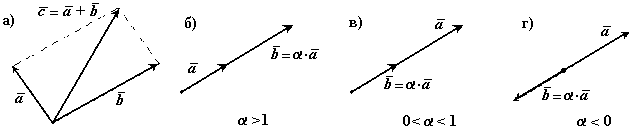
Рисунок 1.2

Праві та ліві системи координат

Декартові системи координат поділяються на два види: праву та ліву.

Розглянемо декартові системи координат на площині (див. рис. 1.3).

При повороті осі Ox правої системи координат на 90^° проти годинникової стрілки вона збігається з віссю Oy.

Розглянемо декартові системи координат у просторі (див. рис. 1.4).

При повороті осі Ox правої системи координат навколо осі Oz на 90^° проти годинникової стрілки вона співпадає з віссю Oy.

Довжина, проекції і напрямні косинуси вектора.

У подальшому будемо розглядати праву систему координат. Одиничні вектори вздовж осей Ox, Oy і Oz утворюють систему одиничних (або базисних) векторів. Будь – який вектор, що має початок у точці О, можна подати як суму числа (a_x, a_y, a_z) – це проекції вектора на осі координат (див. рис. 1.5).

Довжина (або модуль) вектора визначається формулою 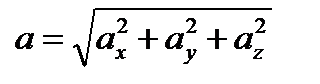і позначається або .

Проекцією вектора на вісь називається скалярна величина, яка визначається відрізком, що відсікається перпендикулярами, опущеними з початку і кінця вектора на цю вісь. Проекція вектора вважається позитивною (+), якщо напрям її збігається з позитивним напрямом осі, і негативною (-), якщо проекція спрямована в протилежну сторону (див. рис. 1.6).

Напрямними косинусами cos(), cos(), cos() вектораназиваються косинуси кутів між вектором і позитивними напрямами осей Ox, Oy і Oz відповідно:

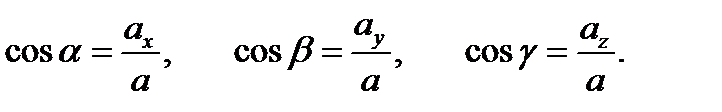
Будь – яка точка простору з координатами (x, y, z) може бути задана своїм радіусом-вектором

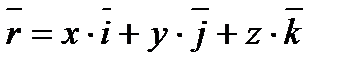
Координати (x, y, z) це проекції вектора на осі координат.

Скалярна множина двох векторів

Є два вектори 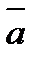і .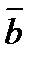

Рисунок 1.7

,

.

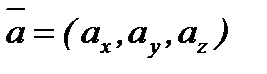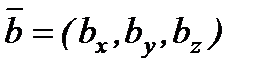Результатом скалярного множення двох векторів 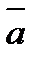і 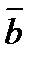є скалярна величина (число). Записується як або 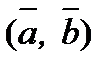. Скалярна множина двох векторівдорівнює .

Властивості скалярної множини:

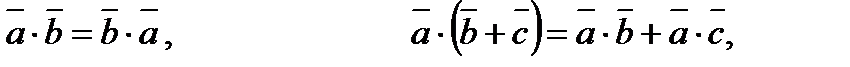
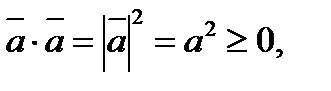
Векторна множина двох векторів

Рисунок 1.8

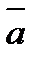Є два вектори і : ,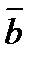

.

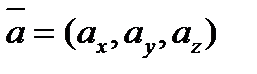Результатом векторного множення двох векторів 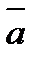і 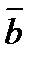є вектор . Записується як або .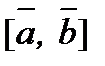

Векторне множення двох векторів – це вектор , перпендикулярний до обох цих векторів і напрямлений так, щоб з його кінця поворот вектора 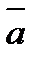до вектора 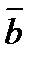було видно проти годинникової стрілки.

Довжина (або модуль) векторного множення дорівнює .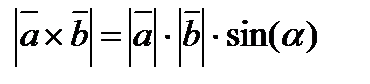

Властивості векторного множення:

Векторне множення двох векторів вираховується через їх проекції таким чином:

.

Лекція 2

Короткий зміст: Основні поняття і визначення статики: матеріальна точка і абсолютно тверде тіло, механічна система, сила, система сил. Аксіоми і теореми статики.

Основні поняття і визначення статики

Матеріальним тілом називається будь – яка кількість речовини, яка заповнює певний об’єм у просторі. Можливі випадки, коли тіло в тих чи інших напрямках має доволі малі розміри порівняно з розмірами в інших напрямках.

Матеріальною точкою називається найпростіша модель матеріального тіла будь – якої форми, розміри якого достатньо малі і яке можна сприйняти за геометричну точку, що має визначену масу.

Механічною дією одного тіла на інше називається така дія, за наявності якої нехтують змінами в хімічній структурі тіла і його фізичному стані. Якщо тіло підлягає механічній дії з боку інших матеріальних тіл, то воно може змінювати свій рух у просторі або залишатися в стані спокою. Механічна дія може проходити як за умови зіткнення тіл, так і на відстані (тяжіння, відштовхування). Отже, під механічною взаємодією розуміють ті дії матеріальних тіл одне на одне, в результаті яких відбувається зміна руху цих тіл або зміна їх форми (деформація).

Механічним рухом називають зміну взаємного положення матеріальних тіл, що відбувається з часом, у просторі.

Механічною системою називається будь – яка сукупність матеріальних точок.

Абсолютно твердим тілом (або незмінною механічною системою)називається матеріальне тіло, геометрична форма якого і розміри не змінюються ні за яких механічних дій з боку інших тіл, а відстань між будь – якими його точками лишається постійною.

Cила – це основна кількісна міра механічної дії одного тіла на інше, яка характеризує її інтенсивність і напрямок.

Природа сили може бути різноманітною. Це можуть бути гравітаційні, електромагнітні, пружні сили або сили тиску. Теоретична механіка не цікавиться природою сил.

Сила визначається точкою прикладання, числовим значенням і напрямком дії, тобто є векторною величиною.

Модуль сили знаходять шляхом її порівняння з силою, взятою за одиницю. У Міжнародній системі одиниць СИ, якою ми будемо користуватися, одиницею сили є 1 н’ьютон (1 Н). Для статичного вимірювання сили існують прилади динамометри.

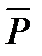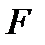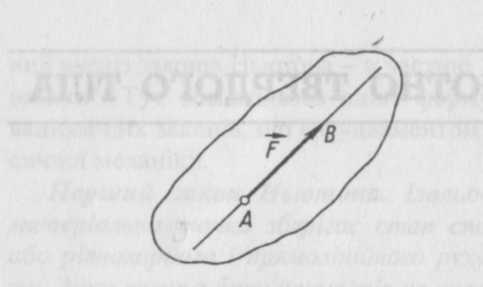
Силу як величину векторну позначають літерою зі знаком вектора (наприклад або ). Для відображення числового значення сили або її модуля використовується знак модуля від вектора або ті ж самі літери, але без знака вектора (наприклад і або і 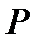). Графічно сила, як і інші вектори, зображується спрямованим відрізком (рис. 2.1). Довжина цього відрізка виражає у вибраному масштабі модуль сили, напрям відрізка відповідає напряму сили, точка А на рис. 2.1 є точкою прикладення сили. Пряма, вздовж якої спрямована сила, називається лінією дії сили.

Рисунок 2.1

Системою сил, називається група сил, котрі діють на тіло що розглядається або (в загальному випадку) на точки механічної системи.

Якщо лінії дії всіх сил лежать в одній площині, то система сил називається пласкою, а якщо ці лінії дії не лежать в одній площині – то система сил називається просторовою.

Системою сил еквівалентною нулю (або врівноваженою системою сил), називається така система сил, дія якої на тверде тіло або матеріальну точку, що знаходиться в стані спокою або рухаються за інерцією, не призводить до зміни стану спокою або руху за інерцією цього тіла або матеріальної точки

.

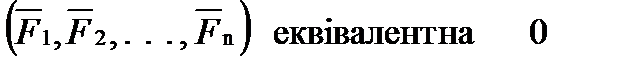Дві системи сил називаються еквівалентними, якщо їх одиничнаа дія на одне й те саме тверде тіло або матеріальну точку однакова за інших рівних умов

.

Рівнодійною силою системи сил що розглядається називається сила, дія якої на тверде тіло або матеріальну точку еквівалентна дії цієї системи сил. Рівнодійну силу зазвичай позначають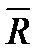

.

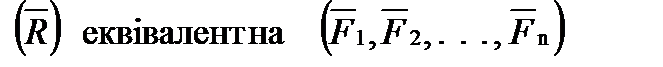Зрівноважувальною силою системи сил, що розглядається, називається сила, додавання якої до заданої системи сил дає нову систему, еквівалентну нулю.

Зрівноважувальна сила дорівнює за модулем рівнодійний і протилежна їй за напрямком.

Сили, що діють на дане тіло (чи систему тіл), можна розділити на зовнішні та внутрішні. Зовнішніми називаються сили, які діють на дане тіло (чи на тіла системи) з боку інших тіл, а внутрішніми – сили, з якими частини цього тіла (чи тіла цієї системи) діють один на одного.

Сила, прикладена до тіла в одній його точці, називається зосередженою. Сили, що діють на всі точки даного об’єму, даної частини поверхні тіла або даної частини кривої, називаються розподіленими.

Поняття про зосереджену силу є умовним. Сили, які в механіці розглядаються як зосереджені, являють собою рівнодійні деяких систем розподілених сил. Зокрема, сила тяжіння, що розглядається в механіці, діє на дане тверде тіло і є рівнодійною сил тяжіння, що діють на його частини. Лінія дії цієї рівнодійної проходить через точку, що називається центром тяжіння тіла. Якщо однорідне тіло має центр симетрії (прямокутний брус, циліндр, куля і т. п.), то центр тяжіння такого тіла знаходиться в його центрі симетрії.

Аксіоми статики

1. Аксіома про рівновагу двох сил. Якщо на вільне абсолютно тверде тіло діють дві сили, то тіло може знаходитися в рівновазі тоді і тільки тоді, коли ці сили рівні за величиною і спрямовані вздовж однієї прямої в протилежні боки.

Рисунок 2.2

,

Рисунок 2.3

2. Аксіома паралелограма сил. Дві сили, прикладені до тіла в одній точці, мають рівнодійну, прикладену в тій самій точці і рівну за величиною і напрямком діагоналі паралелограма, побудованого на (рис. 2.3) цих силах, як на сторонах.

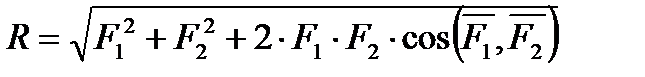
Рисунок 2.4

Ця аксіома допускає і зворотне твердження.

Силу можна розкласти безліччю способів на дві сили, прикладені в будь – якій точці лінії дії даної сили.

Отже, закон паралелограма сил можна ще сформулювати так: дві сили, прикладені до тіла в одній точці, мають рівнодійну, що дорівнює геометричній (векторній) сумі цих сил і прикладену в тій самій точці.

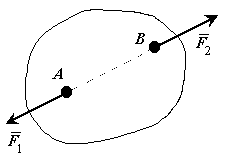
Надалі слід розрізняти поняття суми сил і їх рівнодійної. Пояснимо це прикладом. Розглянемо дві сили і 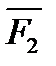(рис. 2.4), прикладені до тіла в точках А і В. Показана на рис. 2.4 сила дорівнює геометричній сумі сил і 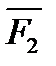(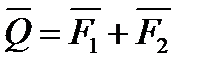) як діагональ відповідного паралелограма. Але сила Q не є рівнодійною цих сил, оскільки неважко зрозуміти, що одна сила Q не може замінити дію сил і 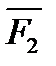на це тіло, де б вона не була прикладена. Надалі буде ще строго доведено, що ці дві сили не мають рівнодійної.

Рисунок 2.5

Правило багатокутника сил. Будь –яке число сил, прикладених в одній точці, можна складати геометрично. Рівнодійну сил (рис. 2.5) визначаємо як векторну суму цих сил:

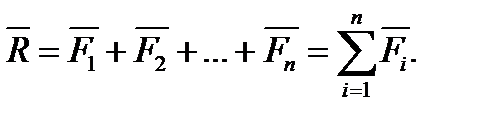
Одержаний таким чином багатокутник називається багатокутником сил, або силовим багатокутником.

3. Аксіома про додавання (відкидання) зрівноваженої системи сил. Якщо на тверде тіло діє система сил, то до неї можна додавати (відкидати) зрівноважену систему сил. Отримана після додавання (відкидання) нова система сил еквівалентна початковій.

Рисунок 2.6

4. Аксіома про рівність дії і протидії. За будь – якої дії одного матеріального тіла на інше має місце така ж за величиною, але протилежна за напрямком протидія.

Якщо до даного тіла прикладена сила дії від другого тіла, то від даного тіла до іншого тіла буде прикладена сила , що дорівнює і прямо протилежна силі . Сили, прикладені в одній геометричній точці, але до різних тіл, не утворюють зрівноваженої системи сил.

Вільним твердим тілом називається тіло, що має можливість отримувати будь – який рух з даного положення, для чого необхідно прикласти відповідну силу.

При розв’язанні більшості задач механіки доводиться мати справу з тілами невільними, тобто позбавленими можливості переміщатися в напрямку дії прикладених до них активних сил. Тіла, що обмежують рух тіла, яке розглядається, називаються в’язями. Сила, з якою в’язь діє на діло, позбавляючи його переміщення в тому чи іншому напрямку, називається силою реакції (протидії) цієї в’язі, або просто реакцією в’язі.

5. Аксіома про в’язі. Ефект від дії в’язей такий самий, як від дії визначених, додаткових сил, котрі можуть бути прикладені до вільного тіла замість в’язей.

Аксіому про в’язі також називають принципом звільнення від в’язей. Відповідно цієї аксіоми, не змінюючи рівноваги тіла, кожну в’язь можна відкинути, замінивши її реакцією в’язі.

Сили, які можуть надавати вільному тілу рух, називаються активними силами. Приклавши до тіла, окрім активних сил, реакції в’язі, можна розглядати тіло як вільне. Активні сили і сили реакції називаються зовнішніми силами.

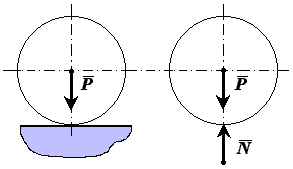
Рисунок 2.7

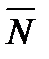Нехай, наприклад, на гладкій нерухомій горизонтальній площині лежить куля (див. рис. 2.6). Площина, що обмежує рух кулі, є для неї в’яззю. Щоб уявно звільнити кулю від в’язі, для утримання її в спокої до неї в точці дотику з площиною необхідно прикласти силу , що дорівнює за модулем в’язі кулі і протилежну їй за напрямком. Сила 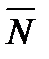і є реакція площини (реакція в’язі). Куля, звільнена від в’язі, буде вільним тілом, на яке діють (активна) сила 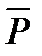, що задається, і реакція площини .

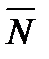6. Аксіома затвердіння. Рівновага механічної системи не порушується від накладання нових в’язей, зокрема, рівновага механічної системи не порушиться, якщо всі частини системи зв’язати між собою незмінно, жорстко.

Дата добавления: 2014-12-16