Розрахунок плоских ферм

Приклад розв’язання задач на рівновагу системи тіл дає розрахунок ферм. Фермою називається жорстка конструкція із прямолінійних стрижнів, що з’єднані між собою шарнірами. Якщо всі стрижні ферми лежать в одній площині,ферму називають плоскою. Місця з’єднання стрижнів ферми називають вузлами.

Рисунок 8.1: а – мостова ферма; б – кроквяна; в – кранова

За своїм призначенням найчастіше ферми поділяють на мостові, кроквяні та кранові (рис.8.1).

При розрахунку ферми тертям у вузлах і вагою стрижнів

(порівняно з зовнішніми навантаженнями) нехтують або розподіляють вагу стрижнів по вузлах. Тоді на кожний із стержнів ферми будуть діяти дві сили, прикладені до їх кінців, які за умови рівноваги можуть бути спрямовані тільки вздовж стрижня. Як наслідок, можна вважати, що стиржневі ферми працюють тільки на розтяг або стиск. Обмежимося розглядом жорстких плоских ферм без зайвих стержнів, що утворені з трикутників. У таких фермах число стиржнів 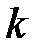і число вузлів 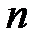пов’язані співвідношенням

.

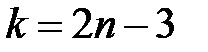Насправді, в жорсткому трикутнику, утвореному з трьох стрижнів, буде три вузли (див., наприклад, на рис. трикутник , утворений стрижнями 4, 5, вузол 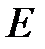– стрижнями 6, 7, і т.д.); як наслідок, для всіх інших (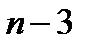) вузлів знадобиться 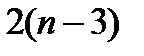стержнів. В результаті число стержнів у фермі 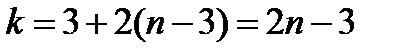. При меншому числі стрижнів ферма не буде жорсткою, при більшому числі вона буде статично невизначною.

Розрахунок ферми зводиться до визначення опорних реакцій і зусиль в її стрижнях.

Опорні реакції можна знайти звичайними методами статики, розглядаючи ферму в цілому як тверде тіло. Перейдемо до визначення зусиль в стрижнях.

Метод вирізання вузлів. Цим методом зазвичай користуються, коли необхідно знайти зусилля в усіх стрижнях ферми. Він зводиться до послідовного розгляду умов рівноваги сил,що сходяться в кожному з вузлів. Хід розрахунків пояснимо на прикладі.

Розглянемо зображену на рис.8.2 ферму, утворену з однакових рівнобедрених трикутників, силу, що діє на ферму, паралельні осі 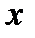і чисельно рівні: .

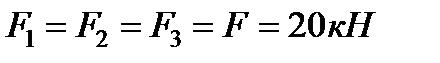У цій фермі число вузлів 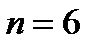, а число стержнів 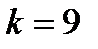. Як наслідок, співвідношення виконується і ферма є жорсткою без зайвих стрижнів.

Складаючи рівняння рівноваги для ферми в цілому, знайдемо, що реакції опор спрямовані, як показано на рисунку, і чисельно рівні:

,

.

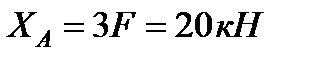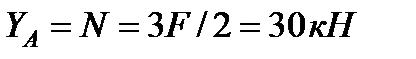Переходимо до визначення зусиль в стрижнях. Пронумеруємо вузли ферми римськими цифрами,а стрижні – арабськими. Шукані зусилля позначимо 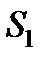(у стрижні 1), 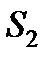(в (стерижні 2) і т.д. Виріжемо уявно всі вузли разом зі стерижнями, що сходяться від ферми. Дію відкинутих стержнів замінимо силами, які будуть спрямовані вздовж відповідних стерижнів, і чисельно дорівнюватимуть шуканим зусиллям Зображаємо одразу відразу всі ці сили на рисунку, спрямовуючи їх від вузлів, тобто вважаючи всі стерижні розтягнутими (рис. 8.2 а; зображену картину потрібно уявити собі для кожного вузла так, як це показано на рис. 8.2 б для вузла ІІІ). Якщо в результаті розрахунку значення зусилля в якому - не будь стерижні буде від`ємним, це буде означати, що даний стерижень не розтягується, а стискається. Літерних позначень для сил, що діють вздовж стержнів, не вводимо, оскільки зрозуміло, що сили, що діють вздовж стерижня 1, дорівнюють чисельно , вздовж стерижня 2, – і т. д.

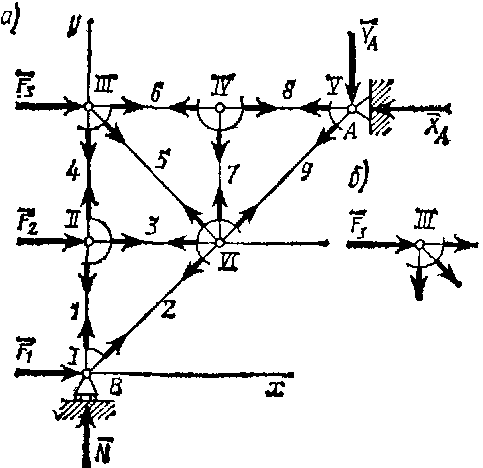
Рисунок 8.2

Тепер для сил, що сходяться в кожному вузлі, складаємо послідовно рівняння рівноваги:

.

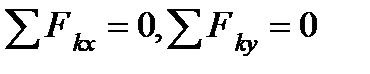Почнемо з вузла І, де сходяться два стерижні, так якоскільки з двох рівнянь рівноваги можна визначити лише два невідомих зусилля.

Складаючи рівняння рівноваги для вузла І, отримаємо:

.

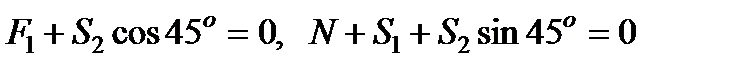Звідси знаходимо:

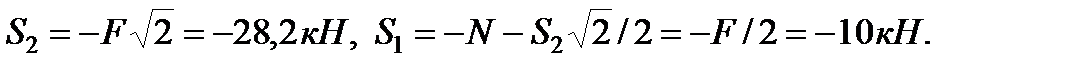Тепер, знаючи 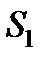, переходимо до вузла ІІ. Для нього рівняння рівноваги дають 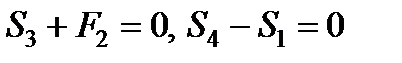, звідки

.

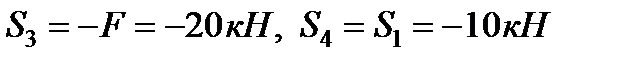Визначивши 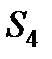, складаємо аналогічним шляхом рівняння рівноваги спочатку для вузла ІІІ, а потім для вузла ІV. З цих рівнянь знаходимо:

.

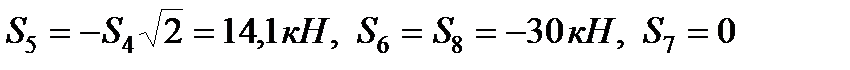Нарешті, для обчислення 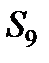складаємо рівняння рівноваги сил, що сходяться у вузлі V, проектуючи їх на вісь 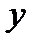. Отримаємо , звідки .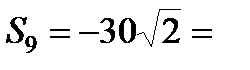

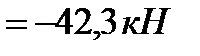Друге рівняння рівноваги для вузла V і два рівняння для вузла VІ можна скласти як перевірочніперевірені. Для знаходження зусиль в стержнях ці рівняння не знадобилисьзнадобилися, так якоскільки замість них були використані три рівняння рівноваги всієї ферми в цілому при визначенн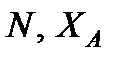і і.і.

Кінцеві результати розрахунку можна звести до у таблиці:

№Номер стерижня
Зусилля, кН	-10	-28,2	-20	-10	14,1	-30		-30	-42,3

Як показують знаки зусиль, стерижень 5 розтягнутий, інші стерижні стиснуті, стерижень 7 не навантажений (нульовий стержень).

Наявність в фермі нульових стержнів, подібних до стерижня 7, виявляється одразу, так якоскількі якщо у вузлі, не навантаженому зовнішніми силами, сходяться три стерижні, із яких два спрямовані вздовж однієї прямої, то зусилля в третьому стерижні дорівнює нулю. Цей результат випливає з рівняння рівноваги проекції на вісь, перпендикулярну до згаданим згаданих двом двох стерижнямів. Наприклад, у фермі, зображеній на рис. 8.3, за відсутності сили 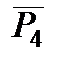нульовим буде стержень 15, і, як наслідок, 13. За наявності ж сили 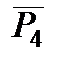ні один з цих стержнів нульовим не є.

Якщо ву ході розрахунку зустрінеться вузол, для якого число невідомих більше двох, то можна використати метод перетинів.

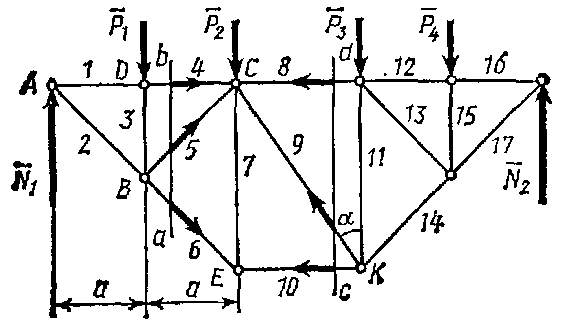
Метод перетинів (метод Ріттера). Цим методом доцільно користуватисяь для визначення зусиль в окремих стерижнях ферми, зокрема для перевірочних розрахунків. Ідея методу полягає в тому, що ферму розділяють на дві частини перетином, що проходить через три стерижні,в яких (або в одному з яких) необхідно визначити зусилля, і розглядають рівновагу однієї з цих частин. Дію відкинутої частини замінюють відповідними силами, спрямовуючи їх вздовж уздовж розрізаних стержнів від вузлів, тобто вважаючи стерижні розтягнутими (як і в методі вирізання вузлів). Потім, складають рівняння рівноваги,беручи центри моментів (або вісь проекцій) так, щоб в у кожне рівняння ввійшло тільки одне невідоме зусилля.

Приклад. Нехай потрібно визначити зусилля в стерижні 6 ферми, зображеної на рис. 8.3. Діючі вертикальні сили 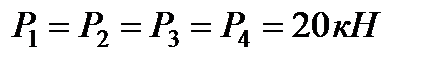, реакції опор 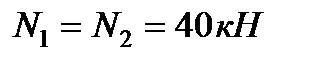. Проводимо перетин 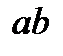через стерижні 4, 5, 6 і розглядаємо рівновагу лівої частини ферми, замінюючи дію на неї правої частини силами, спрямованими вздовж стерижнів 4, 5, 6. Щоб знайти 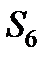,с кладаємо рівняння моментів відносно точки 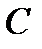, де перетинаються стерижні 4 і 5. Отримаємо, вважаючи 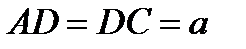і ,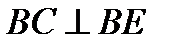

.

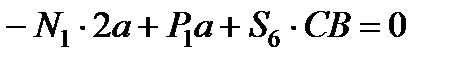Рисунок 8.3

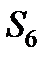Звідси знаходимо . Плече 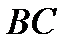визначаємо за даними, що визначають напрямок і розміри стержнів ферми.

В даномуУ цьому приклад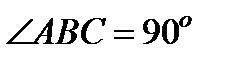і і .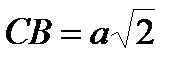

Як наслідок, 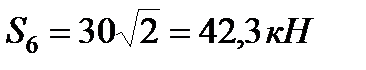, стерижень розтягнутий.

Зусилля в стерижнях 4 і 5 можна знайти, склавши рівняння моментів відносно центрів (точка перетину стержнів 5 і 6) і (точка перетину стержнів 4 і 6).

Щоб визначити зусилля в стерижні 9 тієї ж ферми, проводимо перетин через стерижні 8, 9, 10 і, розглядаючи рівновагу правої частини, складаємо рівняння проекцій на вісь, перпендикулярну до стерижнямів 8 і 10. Отримаємо

,

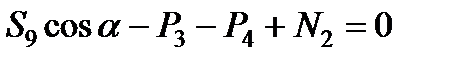звідки знаходимо 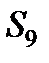. Зусилля в стерижнях 8 і 10 можна в цьому випадку знайти, склавши рівняння моментів відносно центрів 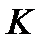і .

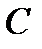КІНЕМАТИКА

Лекція 9

Короткий зміст: Введення в кінематику. Кінематика точки. Поняття траєкторії. Способи завдання руху: векторний, координатний і природний. Швидкість точки при різних способах завдання руху.

Введення. Кінематикою називається розділ теоретичної механіки, в якому вивчаються рухи матеріальних об'єктів, таких, як точка і тверде тіло, без розгляду причин, що викликають або змінюють цей рух. Таке вивчення руху матеріальних об'єктів не вимагає врахування матеріальних характеристик цих об'єктів - маси, моментів інерції і та ін. Рух матеріальних об'єктів завжди відбувається в просторі відносно певної системи відліку і в часі.

Простір вважається тривимірним евклідовим простором, властивості якого не залежать від матеріальних об'єктів, що в ньому рухаються. Час в у класичній механіці не пов'язаний із простором і рухом матеріальних об'єктів. У всіх системах відліку рухомих один відносно одного, воно він протікає проходить однаково. В курсі теоретичної механіки кінематика ділиться на кінематику точки і кінематику твердого тіла.

Кінематика точки

У кінематиці точки розглядаються характеристики руху точки, такі, як швидкість і прискорення, і методи їх визначення при різних способах завдання руху.

Траєкторією точки називається геометричне місце її послідовних положень в просторі з часом відносно даної системи відліку.

Форма траєкторії може бути прямолінійною або криволінійною і залежить від обраної системи координат.

Приклад 1. З літака, що горизонтально летить відносно Землі, скинутий вантаж. Опір повітря відсутній. Траєкторією центру центра мас вантажу відносно системи відліку Oxy, жорстко пов'язаною із Землею, буде парабола. (Рисрис. 1.1а).

Рисунок 9.1

Траєкторією центру центра мас вантажу відносно системи відліку O₁x₁y₁, жорстко пов'язаною з літаком, що летить, буде пряма лінія. (Рисрис. 1.1б).

Приклад 2. Колесо радіусом R котиться по горизонтальній прямій без ковзання. Точка А на ободі колеса здійснює складний рух.

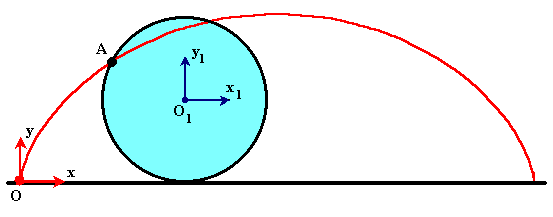
Рисунок 9.2

Траєкторією точки А відносно системи відліку Oxy, жорстко пов'язаною з прямою, буде крива під назвою циклоїда.

Траєкторією точки А відносно системи відліку O₁x₁y₁, яка рухається поступально і початок відліку якої знаходиться в центрі мас колеса, буде коло радіусу радіусом R, центр якого знаходиться в точці O₁.

Дата добавления: 2014-12-16