Координатах. Короткий зміст: Швидкість і прискорення точки в полярних координатах

Лекция 11

Короткий зміст: Швидкість і прискорення точки в полярних координатах.

Швидкість і прискорення точки в полярних

Розглянемо рух точки в площині. В У цьому випадку рух можна задати в полярних координатах. Для цього приймемо візьмемо яку-небудь точку площини за полюс і проведемо з неї полярну вісь, наприклад, вісь Ox. Положення рухомої точки М на плоскості площині відоме, якщо задані радіус r і полярний кут  як функції часу, тобто

і .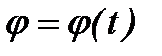

(3.1)

Ці рівняння називаються рівняннями руху точки в полярних координатах. Якщо з рівнянь (3.1) виключити параметр – час t, то отримаємо рівняння траєкторії в полярних координатах: .

Введемо одиничний вектор , направлений напрямлений по радіусу-вектору від полюса О до точки М. Тоді .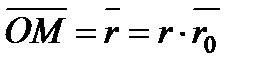

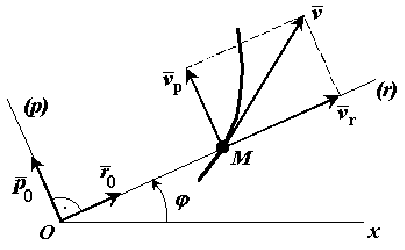
Рисунок 11.1

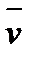Для швидкості отримаємо вираз

Похідна від одиничного вектора за часом рівна дорівнює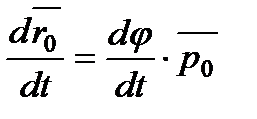

(без доведення) де

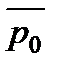– одиничний вектор, напрям якого отримується поворотом вектора на 90⁰ у позитивному напрямі кута.

Після цього для швидкості отримуємо вираз .

Це розкладання швидкості точки на радіальну і трансверсальну (поперечну) складові, тобто

, , ,

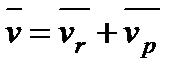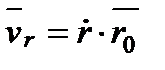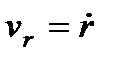– радіальна швидкість;

– трансверсальна швидкість.

Модуль швидкості дорівнює .

Визначимо прискорення точки .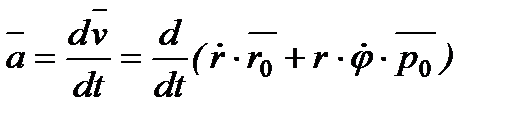

Після диференціювання отримуємо .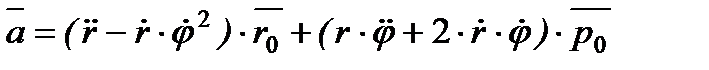

Отримали розкладання прискорення точки на радіальну 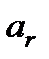і трансверсальну (поперечну) 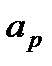складові, тобто

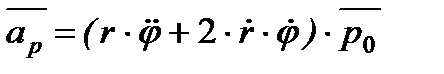
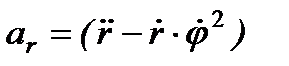- радіальна швидкість;

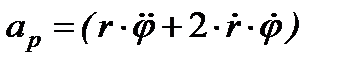– трансверсальна швидкість.

Модуль прискорення дорівнює .

Окремі випадки:

1. Якщо , то маємо прямолінійний рух по прямій Or. В У цьому випадку і

.

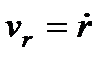
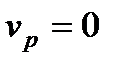
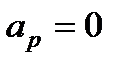
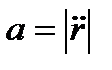2. Якщо 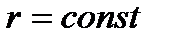, то маємо рух по колу. В цьому випадку и і

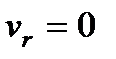
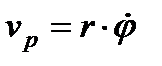
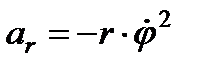
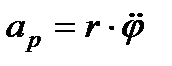
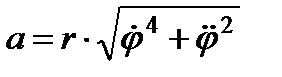
– кутова швидкість обертання радіус-вектора, – його кутове прискорення.

Швидкість і прискорення точки в циліндричних

Дата добавления: 2014-12-16