
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Координатах
|
|
|
|
При русі точки в просторі інколи використовуються циліндричні осі координат.
Положення точки визначається координатами
 , ,  і і 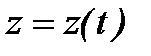
| (3.2) |
Лекція 12
Короткий зміст: Завдання кінематики твердого тіла. Види руху твердого тіла. Число ступенів свободи твердого тіла. Поступальний рух твердого тіла. Обертання твердого тіла навколо нерухомої осі. Кутова швидкість та кутове прискорення твердого тіла.
Кінематика твердого тіла
Абсолютно твердим тілом називається матеріальне тіло, геометрична форма якого і розміри не змінюються ні при яких механічних діях з боку інших тіл, а відстань між будь-якими двома його точками залишається постійною.
Кінематика твердого тіла,також як і динаміка твердого тіла,є одним з найбільш важких складних розділів курсу теоретичної механіки.
Задачі кінематики твердого тіла розпадаються на дві частини:
1. завдання руху і визначення кінематичних характеристик руху тіла в цілому;
2. визначення кінематичних характеристик (траєкторія, швидкість і прискорення) руху окремих точок тіла.
Існує п'ять видів руху твердого тіла:
1. поступальний рух;
2. обертання навколо нерухомої осі;
3. плаский рух;
4. обертання навколо нерухомої точки;
5. вільний рух.
Перші два називаються простими рухами твердого тіла:
Ступені свободи твердого тіла
Числом ступенів свободи твердого тіла називається число незалежних параметрів, які однозначно визначають положення тіла в просторі відносно даної системи відліку.
Рух твердого тіла багато в чому залежить від числа його ступенів свободи.

| Рисунок 12.1 |
Розглянемо приклад. Якщо диск, не обертаючись, може ковзати уздовж нерухомої в даній системі відліку осі (рис.4.1а),то в даній системі відліку він, очевидно, володіє лише одним ступенем свободи – положення диска однозначно визначається,скажімо, координатою x його центруцентра, відлічуваній відлічуваною уподовж вздовж осі. Але якщо диск, крім того, може ще і обертатися (рис.4.1б), то він набуває ще одного ступеню ступеня свободи – до координати x додається кут повороту φ диска довкола навколо осі. Якщо вісь з диском затиснута в рамці, яка може повертатися довкола вертикальної осі (рис. в), то число ступенів свободи стає рівнимдорівнює трьом – до x і φ додається кут повороту рамки φ.
Вільна матеріальна точка в просторі має три ступені свободи: наприклад декартові координати x, y і z. Координати точки можуть визначатись також в циліндричній (r, φ, z) і сферичній (r, φ, ῳ) системах відліку, але число параметрів, що однозначно визначаючих визначають положення точки в просторі завжди три.
Матеріальна точка на плоскості площині має два ступені свободи. Якщо в плоскості площині вибрати систему координат x Оy, то координати x і y визначають положення точки на плоскостіплощині, а координата z тотожно рівна дорівнює нулю.
Вільна матеріальна точка на поверхні будь-якого вигляду має два ступені свободи. Наприклад: положення точки на поверхні Землі визначається двома параметрами: широтою і довготою.
Матеріальна точка на кривій будь-якого виду має один ступінь свободи. Параметром, що визначає положення точки на кривій, може бути, наприклад, відстань уподовж уздовж кривої від початку відліку.
Розглянемо дві матеріальні точки в просторі, сполучені жорстким стрижнем довжини l. Положення кожної точки визначається трьома параметрами, але на них накладена в'язь

| Рисунок 12.2 |
 є рівнянням в'язі. З цього рівняння будь-яка одна координата може бути виражена через останні п'ять координат (п'ять незалежних параметрів). Тому ці дві точки мають (
є рівнянням в'язі. З цього рівняння будь-яка одна координата може бути виражена через останні п'ять координат (п'ять незалежних параметрів). Тому ці дві точки мають ( ) п'ять ступенів свободи.
) п'ять ступенів свободи.
Розглянемо три матеріальні точки в просторі, такі, що не лежать на одній прямій, сполучені трьома жорсткими стрижнями. Число ступенів свободи цих точок рівне дорівнює ( ) шести.
) шести.

| Рисунок 12.3 |
Поступальний рух твердого тіла.
Поступальним рухом твердого тіла називається такий його рух, при якому будь-яка пряма, що жорстко скріплена з тілом, залишається паралельною своєму первинному положенню в кожен момент часу.
Педалі велосипеда поступально рухаються відносно його рами під час руху, поршні в циліндрах двигуна внутрішнього згорання відносно циліндрів, кабіни колеса огляду в парках відносно Землі.
Траєкторії точок в тілі, що поступально рухаються можуть бути не лише прямими, але і й кривими, у тому числі колами.
Теорема. При поступальній поступальному ході русі твердого тіла траєкторії, швидкості таі прискорення всіх точок твердого тіла однакові.

| Рисунок 12.4 |
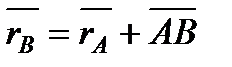 . Траєкторія точки А - це крива, котра задається функцією
. Траєкторія точки А - це крива, котра задається функцією  , а траєкторія точки В - це крива, котра задається функцією
, а траєкторія точки В - це крива, котра задається функцією  . Траєкторія точки В отримується переносом траєкторії точки А в просторі вздовж вектора. Отже, траєкторії всіх точок твердого тіла однакові.
. Траєкторія точки В отримується переносом траєкторії точки А в просторі вздовж вектора. Отже, траєкторії всіх точок твердого тіла однакові.
Продиференціюємо за часом вираз 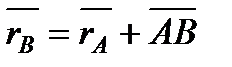 .
.
Отримуємо  , так якоскільки
, так якоскільки  . Продиференціюємо за часом швидкості іта отримаємо вирази
. Продиференціюємо за часом швидкості іта отримаємо вирази  .
.
Отже, швидкості і прискорення всіх точок твердого тіла однакові. щЩо і потрібно було довести.
Поступальнийа хода рух твердого тіла повністю характеризується рухом однієї будь-якої його точки.
Тверде тіло при поступальній поступальному ході русі має три міри ступені свободи.
Для завдання руху твердого тіла в декартовій системі координат досить знати координати 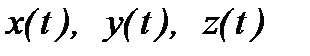 любої будь-якої його точки.
любої будь-якої його точки.
Функції 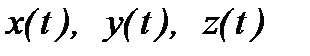 називаються рівняннями поступального руху твердого тіла.
називаються рівняннями поступального руху твердого тіла.
Обертання твердого тіла довкола навколо нерухомої осі
Обертанням твердого тіла довкола навколо нерухомої осі називається такий його рух, при якому дві точки тіла залишаються нерухомими протягом впродовж всього усього часу руху. При цьому також залишаються нерухомими всі точки тіла, розташовані на прямій, що проходить через його нерухомі точки. Ця пряма називається віссю обертання тіла.
Нехай точки A і B нерухомі. Вздовж осі обертання направимо напрямимо ось  . Через ось обертання проведемо нерухому плоскість площину
. Через ось обертання проведемо нерухому плоскість площину  і рухому
і рухому  , скріплену з тілом, що обертається (при
, скріплену з тілом, що обертається (при 
 ).
).

| Рисунок 12.5 |
 і самого тіла визначається двогранним кутом між плоскістю
і самого тіла визначається двогранним кутом між плоскістю  і
і 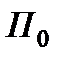 . Позначимо його
. Позначимо його  . Кут
. Кут  називається кутом повороту тіла.
називається кутом повороту тіла.
Положення тіла відносно вибраної системи відліку однозначно визначається у будь-який момент часу, якщо задано рівняння  , де
, де  - любабудь - яка двічі диференційована функція часу. Це рівняння називається рівнянням обертання твердого тіла довкола навколо нерухомої осі.
- любабудь - яка двічі диференційована функція часу. Це рівняння називається рівнянням обертання твердого тіла довкола навколо нерухомої осі.
У тіла, що здійснює обертання довкола навколо нерухомої осі, один ступінь свободи, оскільки його положення визначається завданням лише одного параметра – кута  .
.
Кут  вважається позитивним, якщо він відкладається проти годинникової стрілки, і негативним – в у протилежному напрямі. Траєкторії точок тіла при його обертанні довкола навколо нерухомої осі є колами, розташованими в плоскості площині перпендикулярних осі обертання.
вважається позитивним, якщо він відкладається проти годинникової стрілки, і негативним – в у протилежному напрямі. Траєкторії точок тіла при його обертанні довкола навколо нерухомої осі є колами, розташованими в плоскості площині перпендикулярних осі обертання.
Для характеристики обертального руху твердого тіла довкола навколо нерухомої осі введемо поняття кутової швидкості і кутового прискорення.
Алгебраїчною кутовою швидкістю тіла в будь - який момент часу називається перша похідна за часом від кута повороту у цей момент, тобто 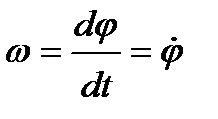 .
.
Кутова швидкість є позитивною величиною при обертанні тіла проти годинникової стрілки, оскільки кут повороту зростає з часом, і негативною – при обертанні тіла за годинниковою стрілкою, тому що кут повороту при цьому убуваєспадає.
Розмірність кутової швидкості за визначенням:  .
.
У техніці кутова швидкість – це частота обертання, виражена в оборотах обертах в за хвилину. За одну хвилину тіло обернеться на кут, де n - – число оборотів обертів в за хвилину. Розділивши цей кут на число секунд в за хвилиніхвилину, отримаємо
 .
.
Алгебраїчним кутовим прискоренням тіла називається перша похідна за часом від кутової швидкості, тобто друга похідна від кута повороту, тобто  .
.
Розмірність кутового прискорення за визначенням:  .
.
Введемо поняття векторів кутової швидкості і та кутового прискорення тіла. 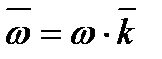 і
і  , де
, де  – одиничний вектор осі обертання. Вектори
– одиничний вектор осі обертання. Вектори  і
і 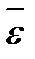 можна зображувати в будь-яких точках осі обертання, вони є ковзними векторами.
можна зображувати в будь-яких точках осі обертання, вони є ковзними векторами.
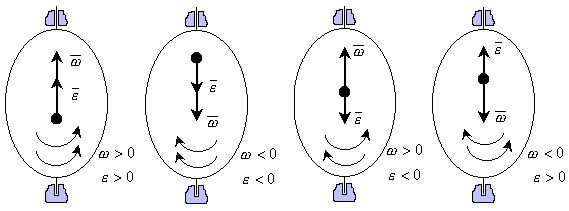
| Рисунок 12.6 |
Кутова алгебраїчна швидкість – це проекція вектора кутової швидкості на вісь обертання. Кутове алгебраїчне прискорення це проекція вектора кутового прискорення швидкості на вісь обертання.
Якщо  при
при  , то алгебраїчна кутова швидкість зростає з часом і, отже, тіло обертається прискорено в даний момент часу в позитивну позитивний сторонубік. Напрями векторів
, то алгебраїчна кутова швидкість зростає з часом і, отже, тіло обертається прискорено в даний момент часу в позитивну позитивний сторонубік. Напрями векторів  і
і 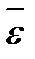 збігаються, отже обидва вони направлені напрямлені в позитивну позитивнний сторону бік осі обертання
збігаються, отже обидва вони направлені напрямлені в позитивну позитивнний сторону бік осі обертання  .
.
При  і
і  тіло обертається прискорено в негативну негативний сторонубік. Напрям векторів
тіло обертається прискорено в негативну негативний сторонубік. Напрям векторів  і
і 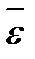 збігаються, обидва вони направлені в негативну сторону осі обертання
збігаються, обидва вони направлені в негативну сторону осі обертання  .
.
Якщо  при
при  , то маємо сповільнене обертання в позитивну позитивний сторонубік. Вектори
, то маємо сповільнене обертання в позитивну позитивний сторонубік. Вектори  і
і 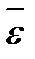 направлені в протилежні сторони.
направлені в протилежні сторони.
Якщо  при
при  , то маємо сповільнене обертання в негативну негативний сторонубік. Вектори
, то маємо сповільнене обертання в негативну негативний сторонубік. Вектори  і
і 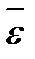 направлені в протилежні сторони.
направлені в протилежні сторони.
Кутову швидкість і кутове прискорення на малюнках рисунках зображують дуговими стрілками довкола навколо осі обертання (якщо не можна зобразити вектори). Дугова стрілка для кутової швидкості вказує напрям обертання тіла, а дугова стрілка для кутового прискорення – напрям, в якому збільшується кутова алгебраїчна швидкість. Для прискореного обертання дугові стрілки для кутової швидкості і та кутового прискорення мають однакові напрями, для сповільненого їхні напрями протилежні.
Окремі випадки обертання твердого тіла
Рівномірне обертання
Обертання називається рівномірним, якщо його кутова швидкість постійна, тобто  .
.
Так якОскільки  , то
, то  . Початкові умови:
. Початкові умови:  , то після інтегрування отримаємо:
, то після інтегрування отримаємо:
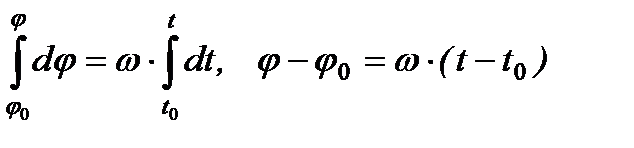 або
або  ,
,
 .
.
Рівнозмінне Рівнозміннюване обертання
Обертання називається рівноприскореним, якщо його кутове прискорення постійне і більше нуля, тобто  .
.
Обертання називається рівносповільненим, якщо його кутове прискорення постійне і менше нуля, тобто 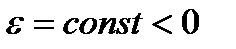 .
.
Так якОскільки 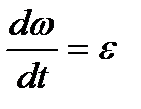 , то
, то 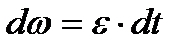 . Початкові умови:
. Початкові умови:  , то після інтегрування отримаємо
, то після інтегрування отримаємо
 або
або 
 ,
,
далі  ,
,  і після інтегрування:,
і після інтегрування:,
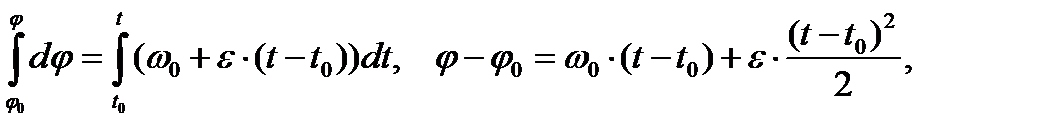 а
а  .
.
Лекція 13
Короткий зміст: Швидкості і та прискорення точок тіла при обертанні. Векторні формули для швидкостей і прискорень точок тіла. Складний рух точки. Абсолютний, відносний і переносний рух точки. Складання швидкостей. Складання прискорень при поступальній поступальному ході русі твердого тіла.
Швидкості і та прискорення точок тіла при обертанні.
Перейдемо до вивчення руху окремих точок твердого тіла. Відоме рівняння обертання твердого тіла довкола навколо нерухомої осі  .
.

| Рисунок 13.1 |
 відбувається елементарний поворот тіла на кут
відбувається елементарний поворот тіла на кут  , то точка М при цьому здійснює уздовж вздовж своєї траєкторії елементарне переміщення
, то точка М при цьому здійснює уздовж вздовж своєї траєкторії елементарне переміщення 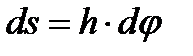 .
.
Тоді алгебраїчна швидкість буде дорівнювати
 або або 
| (5.1) |
Швидкість точки дорівнює  . Швидкість
. Швидкість 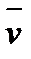 на відміну від кутової швидкості тіла називають інколи ще лінійною, або окружною коловою швидкістю.
на відміну від кутової швидкості тіла називають інколи ще лінійною, або окружною коловою швидкістю.
Модуль швидкості дорівнює
 . .
| (5.2) |
Величини швидкостей точок тіла, при його обертанні довкола навколо нерухомої осі, пропорційні найкоротшим відстаням від цих точок до осі. Коефіцієнтом пропорційності є кутова швидкість  . Швидкості точок направлені напрямлені по дотичних до траєкторій і, отже, перпендикулярні радіусам обертання.
. Швидкості точок направлені напрямлені по дотичних до траєкторій і, отже, перпендикулярні радіусам обертання.
Прискорення точки розкладаємо на дотичну і нормальну складові, тобто
 .
.
Дотичне і нормальне прискорення обчислюються по за формулахформулами:
 ,
,  .
.
Таким чином  ,
,  і модуль прискорення обчислюється за формулою
і модуль прискорення обчислюється за формулою 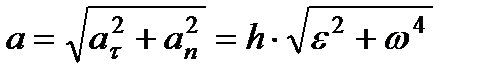 .
.
Дотичні, нормальні іта повні прискорення точок тіла, при його обертанні довкола навколо нерухомої осі, як і швидкості, так само пропорційні найкоротшим відстаням від цих точок до осі. Нормальне прискорення направлене напрямлене по радіусу кола до осі обертання. Напрям дотичного прискорення залежить від знаку кутового прискорення.
Векторні швидкості іта прискорення точок тіла
Швидкість точки по модулю і напряму можна представити подати векторним чином
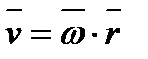 , ,
| (5.3) |
де  –- радіус-вектор точки М, проведений із довільної точки осіи обертання
–- радіус-вектор точки М, проведений із довільної точки осіи обертання  .
.

| Рисунок 13.2 |
Доведення. Вектор  перпендикулярний до площиніплощини, в котрій якій лежать вектори
перпендикулярний до площиніплощини, в котрій якій лежать вектори  і
і  , отже, по за напряму напрямом він збігається зі швидкістю
, отже, по за напряму напрямом він збігається зі швидкістю 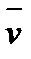 . Модуль векторного добутку
. Модуль векторного добутку 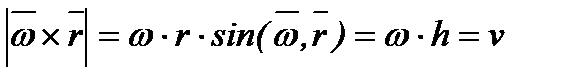 Таким чином, векторний добуток
Таким чином, векторний добуток 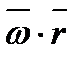 за модулем і напрямом визначає швидкість точки.
за модулем і напрямом визначає швидкість точки.
Визначимо прискорення крапки точки, продиференціювавши формулу Ейлера:.
 , або
, або
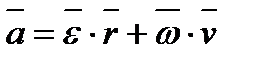
Перший доданок є дотичним прискоренням, а друге – нормальним:.

 .
.
Зіставлення двох формул для швидкості точки ( и і
и і 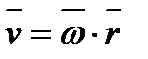 ) дає формулу для обчислення похідної за часом від вектора
) дає формулу для обчислення похідної за часом від вектора  :
:
 .
.
В У цій формулі вектор  має постійний модуль, оскільки сполучає весь час дві точки твердого тіла.
має постійний модуль, оскільки сполучає весь час дві точки твердого тіла.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1393; Нарушение авторских прав?; Мы поможем в написании вашей работы!