Способи завдання руху

Рух точки можна вивчати, використовуючи будь-яку систему координат. Розглянемо три способи завдання руху: векторний, координатний і природний.

Векторний спосіб.

Розглядатимемо випадок декартової прямокутної системи координат. Рух точки відносно даної системи відліку заданий, якщо відомий радіус-вектор 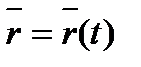цієї точки як функція часу,тобто

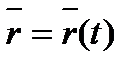
(1-.1)

Векторний спосіб зазвичай застосовується для теоретичного викладу кінематики точки.

Координатний спосіб.

Рух точки можна вивчати використовуючи будь-яку систему координат. Розглянемо випадок декартової прямокутної системи координат.

Рух точки задано, якщо відомі координати точки, як безперервні функції часу,тобто, такі, що двічі диференціюються.:

, , .

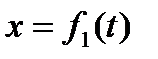(1.2)

Рівняння руху є також рівняння траєкторії точки в параметричній формі. Параметром є час t.

(1.3)

Рівняння траєкторії в координатній формі виходять з рівнянь (1-2) виключенням параметра t. Виходять рівняння двох поверхонь , 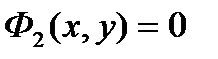. Пересічення цих поверхонь дає криву в просторі – траєкторію точки.

Природний спосіб завдання руху.

При природному способі завдання руху задаються траєкторія точки і закон руху точки по траєкторії. Рух точки розглядається відносно фіксованої системи відліку.

Рисунок 9.3

Для завдання закону руху точки по траєкторії необхідно вибрати на траєкторії точку О, що вважається початком відліку. Крім того, необхідно задати початок відліку часу.:

,

закон руху точки по траєкторії.

Функція 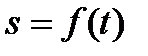має бути безперервною і такою,що двічі диференціюється.

Від завдання руху в декартових координатах можна перейти до його завдання природним способом. Закон руху точки по траєкторії в диференціальній формі через декартові координати виражається у вигляді

.

і після інтегрування – в кінцевій формі

,

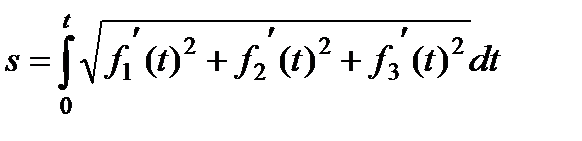якщо .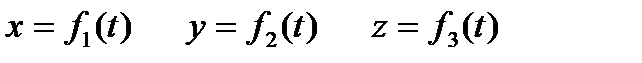

Рисунок 9.4

Швидкість точки

Однією з основних характеристик руху точки є її швидкість відносно вибраної системи відліку.

Швидкість точки при векторному способі завдання руху

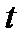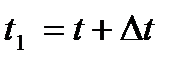Положення точки, що рухається М відносно системи відліку у момент часу , визначається радіусом - вектором .В інший момент часу точка займе положення М ₁ з радіус-вектором . За час 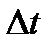радіусом - вектором точки, що рухається, зміниться на .

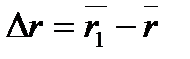Середньою швидкістю 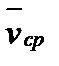називається відношення зміни радіуса - вектора до зміни часу:

. .

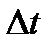(1.4)

Швидкість точки дорівнює першій похідній за часом від її радіус-вектора.

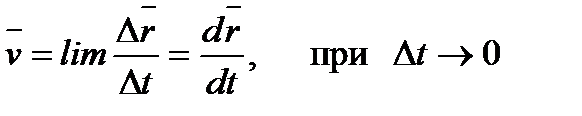
(1.5)

Швидкість точки при координатному способі

Дата добавления: 2014-12-16