Переносного руху

Додавання прискорень в загальному випадку

Теорема. (кінематична теорема Коріоліса) Абсолютне прискоренння точки є векторною сумою трьох прискорень - переносного, відносного і Коріоліса:. .

Доведення. Абсолютне прискоренння точки визначимо обчисленням повної похідної за часом від абсолютної швидкості:

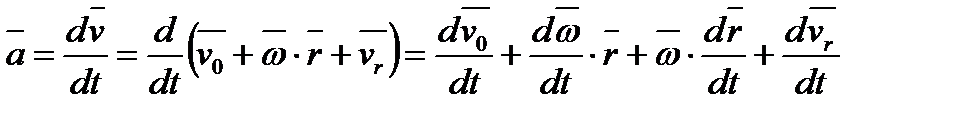
Для похідних від векторів и 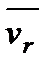застосуємо формулу Бура. Отримаємо

, .

Враховуючи, що , , , , отримаємо для абсолютного прискорення

(15.8)

В У цій формулі перші три складові є переносним прискоренням для точки 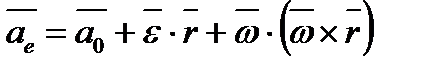. Остання складова називається прискоренням Коріоліса (іноді його називають додатковим або поворотним прискоренням) і обчислюється .

У підсумку формула (9.8) приймає виднабуває вигляду

(15.9)

Що що і й треба було довести.

Прискорення Коріоліса

Теорема (Правило Жуковського). Щоб отримати напрямок прискорення Коріоліса, необхідно вектор проекції відносної швидкості повернути на навколо осі, паралельної осі переносного обертання в направленні напряміцього обертання.

Модуль прискорення Коріоліса дорівнює подвоєному добутку кутової швидкості переносного обертання на модуль проекції відносно швидкості на плоскістьплощину, перпендикулярну осі переносного обертання:

Спроектувавши обидві частини рівності на рухомі осі координат, одержимо вирази для проекцій коріолісового прискорення:

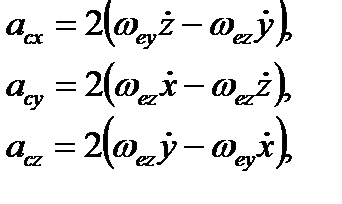
де , , 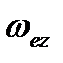– проекції кутової швидкості на осі координат; , , – проекції відносної швидкості на ці самі осі координат. Тоді модуль коріолісового прискорення

.

Напрям визначається за напрямними косинусами кутів, які вектор утворює відповідно з ортами рухомих осей:

Випадки перетворення на нуль коріолісового прискорення. Коріолісове прискорення дорівнює нулю в ті моменти (або на тих проміжках часу), коли:

1) вектор дорівнює нулю, тобто переносний рух є поступальним;

2) відносна швидкість дорівнює нулю, тобто немає відносного руху;

3) , тобто коли вектори і є колінеарними.

Фізичні причини виникнення коріолісового прискорення. Коріолісове прискорення виникає внаслідок двох причин:

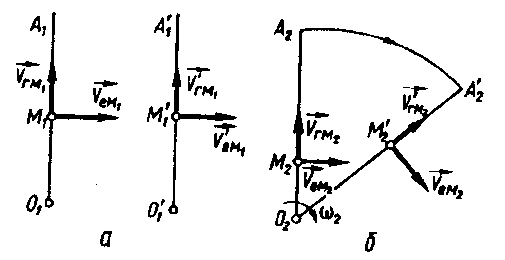
Рисунок 15.3

1. Уявімо Уявимо собі два прямолінійних відрізки О₁А₁ та О₂А₂, по яких рухаються точки М₁ і М₂ (рис. 15.3). Відрізок О₁А₁ рухається поступально, а відрізок О₂А₂ обертається навколо точки О₂. Позначимо через та відповідно відносну та переносну швидкості точки М. Переносним рухом точки М₁ (рис. 15.3, а) є поступальний рух, зумовлений рухом відрізка. Через елементарний проміжок часу відрізок О₁А₁ займе положення 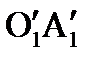. Оскільки переносний рух – поступальний, то переносні швидкості М₁ і 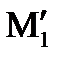однакові.

Переносним рухом точки М₂ (рис. 15.3, б) є обертальний рух, спричинений обертанням відрізка О₂А₂ навколо точки О₂. Тому переносні швидкості точки М₂ на відрізку О₂А₂ та різні: ; .

Отже переносна швидкість точки М₂ змінюється залежно від її відносного руху вздовж відрізка О₂А₂. При цьому швидкість змінення зміни переносної швидкості точки М₂ у часі, яка створює додаткове прискорення, пропорційна відносній швидкості 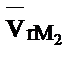та кутовій швидкості переносного руху .

2. Відносна швидкість точки М₂, тобто 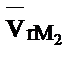, залежить від переносного обертального руху, оскільки при обертанні відрізка О₂А₂ змінюється напрям відносної швидкості 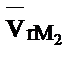(рис. 15.3, б).

Отже, швидкість змінення зміни в часі відносної швидкості точки (тобто прискорення точки, яке залежить від наведеної вище причини) також буде пропорційною відносній швидкості 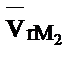та кутовій швидкості переносного руху.

Таким чином, коріолісове прискорення характеризує змінення зміну в часі відносної швидкості через переносний непоступальний рух і переносної швидкості – через відносний рух точки.

Лекція 16

Короткий зміст: Синтез рухів. Пара обертань. Додавання поступального і обертального рухів.

Складний рух твердого тіла.

Постановка задачі синтезу рухів.

Дотепер ми займалися аналізом рухів: прагнучиі вивчити складний рух, ми розкладали його на простіші рухи. Часто виникає обернена задача, або задача синтезу чи складання рухів: утворити (побудувати та вивчити) складний рух тіла з простіших рухів. Постановка задачі: в кожний даний момент часу при різних часткових припущеннях про характер відносного та переносного рухів знайти вигляд того результуючого складного руху, якому відповідає розподіл абсолютних швидкостей точок тіла в цей момент. Тобто мова йтиме про складання миттєвих (нескінченно малих) переміщень тіла.

Оскільки розподіл швидкостей точок твердого тіла в даний момент залежить від його поступальної і кутової швидкостей в у цей момент, то цю таку задачу можна ще назвати задачею про складання векторів миттєвих поступальних і кутових швидкостей тіла. Складові рухи комутативні в тому сенсі, що миттєвий розподіл швидкостей результуючого руху не зміниться, якщо відносний і переносний рухи поміняти місцями.

Введемо нерухому систему координат . Нехай тверде тіло (Р) рухається відносно системи координат , яка, в у свою чергу, переміщується відносно системи . У цьому випадку кажутьговорять, що тіло здійснює складний рух, який складається з двох складових рухів (рис. 16.1).

У більш загальних випадках складний рух може складатись з n складових рухів. При цьому маємо n систем координат і задається n рухів: рух тіла відносно системи координат 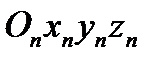, рух системи відносно системи і т. д. Нарешті задається рух системи відносно нерухомої системи . Рух тіла або рух якої-небудь однієї системи координат відносно іншої в загальному випадку нічим не обмежено. Задача полягає в знаходженні залежностей між основними характеристиками складових рухів і складного руху.

Додавання поступальних рухів

Рисунок 16.1

Нехай система на рис. 16.1 рухається поступально відносно нерухомої системи координат зі швидкістю . Через позначимо швидкість поступального руху тіла (Р) відносно системи . Тоді рух тіла відносно системи є складним: його рух стосовно відносно тріедра можна трактувати як відносний (), а рух тріедра стосовно тріедра є переносним . Рух точки 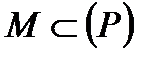відносно системи є абсолютним, швидкість цього руху можна знайти за формулою. Оскільки , то

.

Таким чином, абсолютні швидкості всіх точок тіла виявилися однаковими. Отже, при додаванні поступальних рухів твердого тіла результуючий рух буде також поступальним. Швидкість результуючого руху дорівнює сумі швидкостей складових рухів. Для n поступальних рухів:

.

Коли дві складові руху є поступальними, то (на відміну від усіх наступних випадків) теорема про додавання швидкостей формулюється і доводиться однаково як для миттєвих, так і для скінченних переміщень.

Рух, в якому швидкості всіх точок тіла тільки в даний момент часу виявляються рівними між собою, називається миттєво поступальним. Прискорення точок при цьому різні.

Дата добавления: 2014-12-16