
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поняття про фазову площину
|
|
|
|
Звичайний опис руху системи з одним ступенем свободи у вигляді залежності координати від часу  не являється є єдино можливим. У ряді випадків, особливо при вивченні нелінійних механічних коливань, певні достоїнства має представлення руху на фазовій площині. Стан системи у будь-який фіксований момент часу
не являється є єдино можливим. У ряді випадків, особливо при вивченні нелінійних механічних коливань, певні достоїнства має представлення руху на фазовій площині. Стан системи у будь-який фіксований момент часу  визначається парою відповідних значень
визначається парою відповідних значень 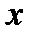 та
та 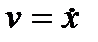 і може бути представлено представлений зображаючоюзображальною (фазовою) точкою в плоскій декартовій системі координат
і може бути представлено представлений зображаючоюзображальною (фазовою) точкою в плоскій декартовій системі координат 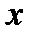 ,
,  , якщо відкладати по осі абсцис координату
, якщо відкладати по осі абсцис координату 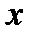 , а по осі ординат - – швидкість
, а по осі ординат - – швидкість  . Така площина називається фазовою. В процесі руху даної системи величини
. Така площина називається фазовою. В процесі руху даної системи величини 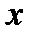 та
та  змінюються і, відповідно, міняється змінюється положення зображуючої зображальної точки на фазовій площині. Геометричне місце зображуючих зображальних точок для цього руху називається фазовою траєкторією.
змінюються і, відповідно, міняється змінюється положення зображуючої зображальної точки на фазовій площині. Геометричне місце зображуючих зображальних точок для цього руху називається фазовою траєкторією.
Для побудови фазової траєкторії при заданому законі руху  треба необхідно шляхом диференціювання утворити вираження швидкості
треба необхідно шляхом диференціювання утворити вираження швидкості 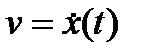 , а потім виключити час із двох рівнянь:
, а потім виключити час із двох рівнянь:  ,
,  .
.
Функція 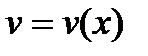 і описує фазову траєкторію цього руху.
і описує фазову траєкторію цього руху.
Фазова площина особливо зручна для представлення коливальних процесів, коли координата і швидкість не виходять за відомі межі; по-цьомутому уся вся картина руху навіть впродовж необмеженого часу займає обмежену частину фазової площини.
Сукупність фазових траєкторій, яка описує усі всі можливі рухи цієї системи, називається фазовою діаграмою (фазовим портретом) цієї системи.
Для вільних гармонійних гармонічних коливань  , а
, а 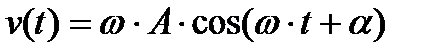 . Виключаючи з цих виразів час
. Виключаючи з цих виразів час  ,отримуємо
,отримуємо

| Рисунок 18.3 |
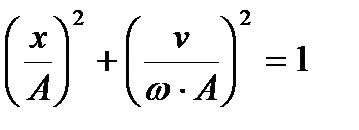 .
.
Це рівняння еліпса. Його півосі залежать від амплітуди і кругової колової частоти.
Вільні коливання в полі постійної сили.
На матеріальну точку, окрім пружної сили, діє сила, постійна за величиною і напрямом.
| Рисунок 18.4. |
 Позначимо її
Позначимо її 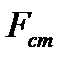 ,тоді диференціальне рівняння руху точки прийме набере видвигляду:
,тоді диференціальне рівняння руху точки прийме набере видвигляду: 
або  ,
,
де 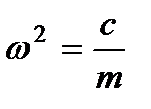 .
.
Початкові умови приймають виднабирають вигляд: при 
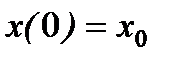 ,
,  .
.
Це неоднорідне диференціальне рівняння. Його рішення розв’язок складається з рішення розв’язку однорідного диференційного диференціального рівняння і частки рішення розв’язку неоднорідного диференціального рівняння  .
.
Рішення Розв’язок має вигляд:
 ,
,
 ,
,
 ,
,  ,
,
 .,
.,
Якщо початок відліку координати зрушити змістити на 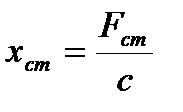 ,
, 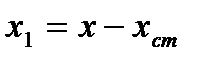 , тоді в новій системі відліку рішення розв’язок матиме вигляд:
, тоді в новій системі відліку рішення розв’язок матиме вигляд:
 ,
,
 ,
,
 – амплітуда коливань.;
– амплітуда коливань.;
| Рисунок 18.5 |
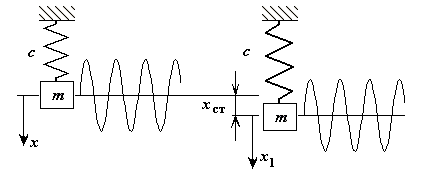
Паралельне включення пружних елементів

| Рисунок 18.6 |
Маса закріплена за допомогою двох пружних елементів розташованих паралельно.
Змістимо масу на відстань 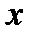 .
.  ,
,  ,
,  .
.
Результуюча жорсткість пружних елементів, розташованих паралельно, дорівнює сумі жорсткостей цих елементів.
Послідовне включення пружних елементів

| Рисунок 18.7 |
Змістимо масу на відстань 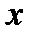 . У пружних елементах виникає (пружна) сила
. У пружних елементах виникає (пружна) сила  , однакова для обох елементів. Перший пружний елемент змінить
, однакова для обох елементів. Перший пружний елемент змінить 
| Рисунок 18.8 |
 , другий – на.
, другий – на. 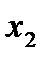 .
.  ,.
,.
 ,
,  ,
,  .
.
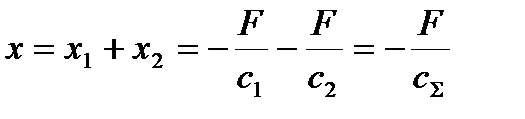 , отже,
, отже, 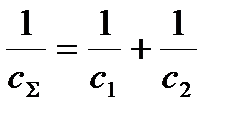 .
.
Зворотній Зворотна величина результуючої жорсткості пружних елементів рас-покладених розміщених послідовно дорівнює сумі зворотних величин жорсткостей цих елементів.
Зворотній Зворотна величина жорсткості пружного елемента називається податливістю цього елемента:.
 ,
,  ,
, 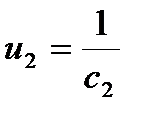 ,
, 
Результуюча підодатливість пружних елементів розташованих по-отжепослідовно дорівнює сумі піоддатливоістіь цих елементів.
Вимушені коливання без опору
Розглянемо рух точки під дією двох сил: одна відновлювальналююча, інша залежить від часу  . – гармонічйна компенсуюча компенсувальна сила.
. – гармонічйна компенсуюча компенсувальна сила.

| Рисунок 18.9 |
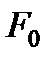 – амплітуда вимушених змушених коливань;.
– амплітуда вимушених змушених коливань;.
 – кругова колова частота вимушених змушених коливань.
– кругова колова частота вимушених змушених коливань.
Диференціальне рівняння руху точки з масою  , закріпленною на пружному елементі, під дією збурююючоївальної гармонійної гармонічної сили має вигляд:
, закріпленною на пружному елементі, під дією збурююючоївальної гармонійної гармонічної сили має вигляд:
 .
.
Задаючи рішення рівняннярозв’язок у вигляді: 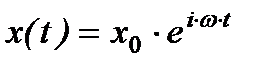 і підставляючи його в диференціальне рівняння, отримаємо алгебраїчне рівняння для визначення амплітуди вимушених коливань.
і підставляючи його в диференціальне рівняння, отримаємо алгебраїчне рівняння для визначення амплітуди вимушених коливань.
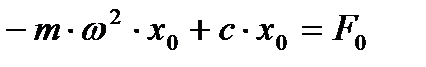 .
.
Розділимо його на масу і позначимо  , тоді
, тоді  і остаточно
і остаточно
 - – амплітуда вимушених змушених коливань;.
- – амплітуда вимушених змушених коливань;.
 – частота власних коливань
– частота власних коливань
Матеріальна точка коливається з амплітудою  і частотою збурюючої збурювальної сили
і частотою збурюючої збурювальної сили  .
.
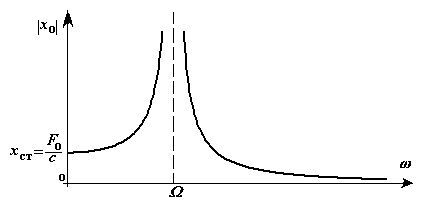
| Рисунок 18.10 |
 від частоти вимушених змушених коливань
від частоти вимушених змушених коливань  .
.
Модуль амплітуди вимушених змушених коливань зростає від 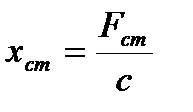 (при
(при  ) до нескінченності (при
) до нескінченності (при  ) і убуває від нескінченності
) і убуває від нескінченності
(при  ) до нуля (при
) до нуля (при  ).
).
Явище, коли частота вимушених змушених коливань збігається з власною частотою коливань системи, називається резонансом.
Вільні коливання з в'язким опором
Існують пристрої (демпфери), які створюють силу, пропорційну відносній швидкості.  . Коефіцієнт пропорційності називається коефіцієнтом демпфування, або коефіцієнтом в'язкого опору.
. Коефіцієнт пропорційності називається коефіцієнтом демпфування, або коефіцієнтом в'язкого опору.

| Рисунок 18.11 |

 або
або 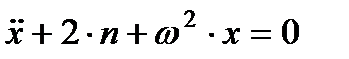 ,
, 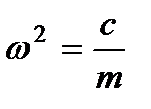 ,
, 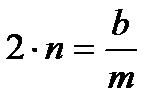 .
.
Початкові умови мають вигляд: 
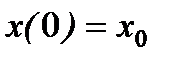 ,
, 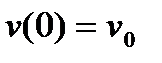 .
.
Характеристичне рівняння має вигляд:  .
.
Коріння Корені характеристичного рівняння рівні:  .
.
Розглянемо можливі можливий рішення:розв’язок:
1-й випадок 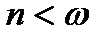
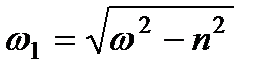 ,
,  .
.
Рішення Розв’язок має вигляд:
 ,
,
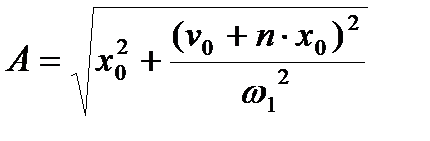 ,
,  - – умовна амплітуда затухаючих згасаючих коливань;
- – умовна амплітуда затухаючих згасаючих коливань;
| Рисунок 18.12 |

 – кругова колова, або циклічна, частота затухаючих згасаючих коливань вимірюється в
– кругова колова, або циклічна, частота затухаючих згасаючих коливань вимірюється в  .
.
 – фазовий кут (або просто фаза).
– фазовий кут (або просто фаза).  .
.
 – період затухаючих згасаючих коливань.
– період затухаючих згасаючих коливань. 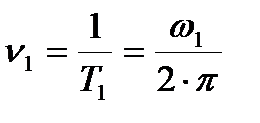 – частота коливань (1 колив/cек=1 Гц)
– частота коливань (1 колив/cек=1 Гц)
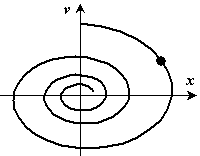
| Рисунок 18.13 |
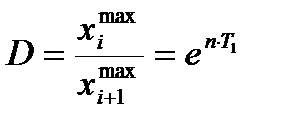 – декремент коливань.
– декремент коливань.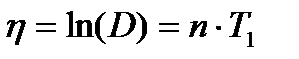 - логарифмічний декремент коливань.
- логарифмічний декремент коливань.
Матеріальна точка здійснює гармонічні коливання з частотою  і амплітудою, величина якої весь час зменшується.
і амплітудою, величина якої весь час зменшується.
Рух зображуючої зображувальної точки на фазовій площині показано на
2-й випадок: 

 .
.
Рішення Розв’язок має вигляд:
 . Матеріальна точка здійснює затухаючий згасаючих не коливальний рух.
. Матеріальна точка здійснює затухаючий згасаючих не коливальний рух.

| Рисунок 18.14 |
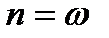 ,
, 
(два однакових кореня)
Рішення Розв’язок має вигляд:
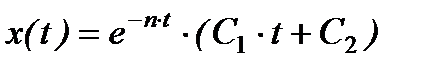 .
.
Матеріальна точка так само робить загасаючий не коливальний рух.
Вимушені Змушені коливання з в'язким опором
Розглянемо рух точки під дією трьох сил: одна відновлююча сила, друга інша – сила демпфування (сила в'язкого опору), а третя залежить від часу.  – гармонійна гармонічна збурююча збурювальна сила;.
– гармонійна гармонічна збурююча збурювальна сила;.

| Рисунок 18.15 |
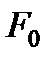 –- амплітуда вимушених змушених коливань.
–- амплітуда вимушених змушених коливань.
 -
-  – кругова частота вимушених змушених коливань.
– кругова частота вимушених змушених коливань.
Диференціальне рівняння руху точки з масою  , закріпленої на пружному елементі і демпфері, під дією збурюючої збурювальної гармонійної гармонічної сили має вигляд:
, закріпленої на пружному елементі і демпфері, під дією збурюючої збурювальної гармонійної гармонічної сили має вигляд:  .
.
Задаючи рішення розв’язок рівняння у вигляді 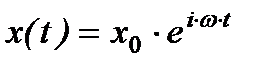 і підставляючи його в диференціальне рівняння, отримаємо алгебраїчне рівняння для визначення амплітуди вимушених коливань
і підставляючи його в диференціальне рівняння, отримаємо алгебраїчне рівняння для визначення амплітуди вимушених коливань  .
.
Розділимо його на масу і позначимо  ,
, 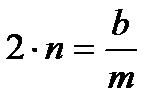 , тоді
, тоді  і остаточно
і остаточно
 – амплітуда вимушених змушених коливань.
– амплітуда вимушених змушених коливань.
 – частота власних коливань.
– частота власних коливань.

| Рисунок 18.16 |
Матеріальна точка коливається з амплітудою
 і частотою компенсуючої компенсувальної сили
і частотою компенсуючої компенсувальної сили  . Побудуємо залежність модуля амплітуди
. Побудуємо залежність модуля амплітуди  від частоти збурюючої збурювальної сили
від частоти збурюючої збурювальної сили  .
.
Модуль амплітуди вимушених змушених коливань зростає від 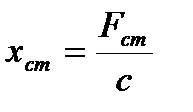 (при
(при  ) до деякої величини, а потім спадає до нуля (при
) до деякої величини, а потім спадає до нуля (при  ).
).
Лекція 19
Короткий зміст: Загальні теореми динаміки точки. Кількість руху точки. Елементарний і повний імпульс сили. Теорема про зміну кількості руху точки. Момент кількості руху точки. Теорема про зміну моменту кількості руху точки. Робота сили. Потужність. Кінетична енергія точки. Теорема про зміну кінетичної енергії точки. Принцип Даламбера для матеріальної точки.
Загальні теореми динаміки
Для вирішення багатьох завдань динаміки замість безпосереднього інтегрування диференціальних рівнянь руху більш ефективно користуватися так званими загальними теоремами, які є наслідком основного закону динаміки.
Кількість руху точки
Кількістю руху матеріальної точки 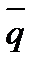 називається вектор, рівний що дорівнює добутку маси точки
називається вектор, рівний що дорівнює добутку маси точки  на її швидкість
на її швидкість  :
:
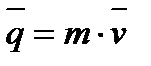 .
.
Кількість руху точки у фізиці часто називають імпульсом матеріальної точки.
Проекції кількості руху точки на прямокутні декартові осі координат рівні:
 ,
, 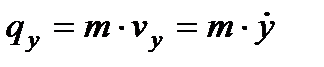 ,
,
 .
.
Одиницею виміру кількості руху в СІ є  .
.
Елементарний і повний імпульси сили.
Дія силі сили 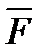 на матеріальну точку в період часу
на матеріальну точку в період часу 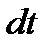 можна охарактеризувати елементарним імпульсом силі сили
можна охарактеризувати елементарним імпульсом силі сили  .
.
Повний імпульс сили 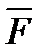 за час
за час 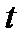 , або імпульс сили
, або імпульс сили 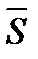 , визначається за формулою
, визначається за формулою 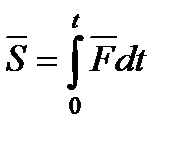 . (Повний інтеграл за час
. (Повний інтеграл за час 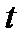 від елементарного імпульсу).
від елементарного імпульсу).
У окремому випадку, якщо сила 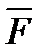 постійна і за величиною, і за напрямком (
постійна і за величиною, і за напрямком (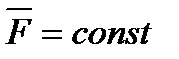 ),
),  .
.
Проекції імпульсу сили на прямокутні декартові осі координат рівні:



Одиницею виміру імпульсу в СІ є – 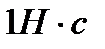 .
.
Теорема про зміну кількості руху точки.: Похідна за часом від кількості руху точки дорівнює силі, що діє на точку.
Запишемо основний закон динаміки  у вигляді
у вигляді  .Оскільки маса постійна, то внесемо її під знак похідної. Тоді
.Оскільки маса постійна, то внесемо її під знак похідної. Тоді
 , ,
| (19.1) |
що і потрібно довести.
У проекціях на координатні осі рівняння (19.1) можна представити подати у вигляді:
 ,
,  ,
,  .
.
Теорема імпульсів (у диференціальній формі). Диференціал від кількості руху точки дорівнює елементарному імпульсу сили, що діє на точку.
Помножимо ліву і праву частині частини рівняння (19.1) на 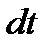 і отримаємо
і отримаємо
 . .
| (19.2) |
В У проекціях на координатні осі отримуємо:
 ,
,
 ,
,
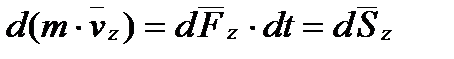 .
.
Теорема імпульсів (у інтегральній формі). Зміна кількості руху точки за який-небудь проміжок часу дорівнює імпульсу сили за цей же самий проміжок часу.
Інтегруючи обидві частини рівняння (19.2) за часом в межах від нуля до 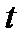 ,отримуємо:
,отримуємо:
 .
.
В У проекціях на координатні вісі осі отримуємо:
 ,
,
 ,
,
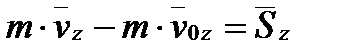 .
.
Момент кількості руху точки.
У деяких завданнях в якостіяк динамічної динамічну характеристики характеристику точки, що рухається, замість самої кількості руху розглядають його момент відносно якого-небудь центрау або осі. Ці моменти визначаються також, як і моменти сили.
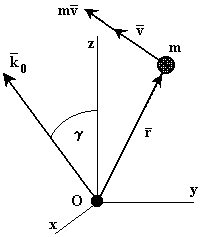
Рисунок 19.1
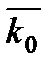 відносно деякого центру центра О називається вектор, що визначуваний визначається рівністю
відносно деякого центру центра О називається вектор, що визначуваний визначається рівністю
 .
.
Момент кількості руху точки називають також кінетичним моментом.
Момент кількості руху відносно якої-небудь осі  , що проходить через центр О, дорівнює проекції вектору вектора кількості руху
, що проходить через центр О, дорівнює проекції вектору вектора кількості руху 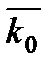 на цю вісь
на цю вісь 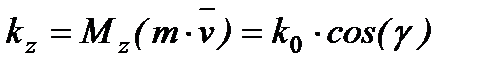 .
.
Якщо кількість руху  задано своїми проекціями
задано своїми проекціями  на осі координат і дані координати
на осі координат і дані координати  точки
точки  в у просторі, то момент кількості руху
в у просторі, то момент кількості руху 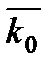 відносно початку координат обчислюється таким чином:
відносно початку координат обчислюється таким чином:
 Проекції моменту кількості руху
Проекції моменту кількості руху 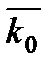 на осі координат рівні:
на осі координат рівні:
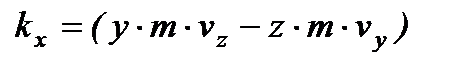 ,
,
 ,
,
 .
.
Одиницею виміру кількості руху в СІ є
 .
.
Теорема про зміну моменту кількості руху точки: Похідна за часом від моменту кількості руху точки, в узятого відносно якого-небудь центруцентра, дорівнює моменту діючої на точку сили відносно того ж центру.
 .
.
Доведення:
Продиференціюємо момент кількості руху за часом 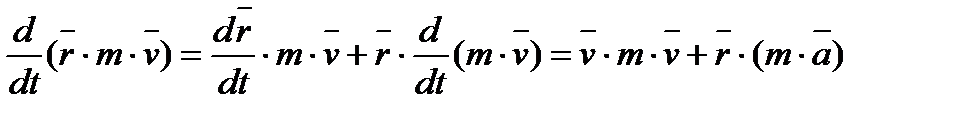 ,
,
 ,
,  , отже
, отже
 , ,
| (19.3) |
що і потрібно довести.
Теорема. Похідна за часом від моменту кількості руху точки, вузятого відносно якої-небудь осі, дорівнює моменту сили, що діє на точку, відносно тієї ж осі.
Для доказу доведення досить спроектувати векторне рівняння (19.3) на цю вісь. Для оси  це буде виглядати мати такий вигляд так:
це буде виглядати мати такий вигляд так: 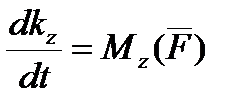
Наслідки з теорем:
1. Якщо момент сили відносно точки дорівнює нулю, то момент кількості руху відносно цієї точки – величина постійна.  ,
, 
 .
.
2. Якщо момент сили відносно осі дорівнює нулю, то момент кількості руху відносно цієї осі величина постійна:.
 ,
, 
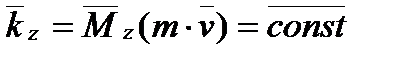 .
.
Робота сили. Потужність.
Одна з основних характеристик сили, що оцінюють дію сили на тіло при деякому його переміщенні.

| Рисунок 19.2 |
 .
.  ,
, 
Одиницею виміру роботи в СІ є 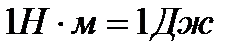 .
.
При  , при
, при 
Окремі випадки:  ,
,


Елементарне переміщення дорівнює диференціалу радіусу векторау точки додатка сили.
Елементарна робота сили дорівнює скалярному твору добутку сили на елементарне переміщення або на диференціал радіусау вектору вектора точки прикладення сили:
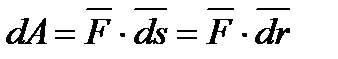 .
.
Елементарна робота сили дорівнює скалярному твору добутку елементарного імпульсу сили на швидкість точки.
 .
.
Якщо сила 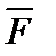 задана своїми проекціями (
задана своїми проекціями ( ) на осі координат і елементарне переміщення задано своїми проекціями (
) на осі координат і елементарне переміщення задано своїми проекціями ( ) на осі координат, то елементарна робота сили рівнадорівнює:
) на осі координат, то елементарна робота сили рівнадорівнює:
 (аналітичне вираження елементарної роботи).
(аналітичне вираження елементарної роботи).
Робота сили на будь-якому кінцевому переміщенні  дорівнює узятому взятому уздовж цього переміщення інтегралу від елементарної роботи:.
дорівнює узятому взятому уздовж цього переміщення інтегралу від елементарної роботи:.
 .
.
Потужністю сили називається величина, що визначає роботу, що здійснюється силою в одиницю часу. У загальному випадку потужність дорівнює першій похідній за часом від роботи.
 ,
,  .
.
Потужність дорівнює скалярному твору добутку сили на швидкість.
| Рисунок 19.3 |
 .
.
У техніці за одиницю сили береться беруть 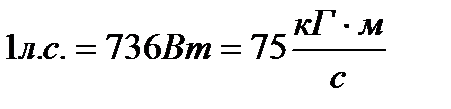 .
.
Приклад 1. Робота сили тяжіння.
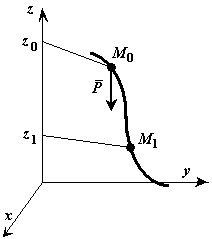
Нехай точка М, на яку діє сила тяжіння Р, переміщається з положення 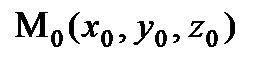 в положення
в положення  . Виберемо осі координат так, щоб вісь
. Виберемо осі координат так, щоб вісь  була спрямована вертикально вгору.
була спрямована вертикально вгору.
Тоді,,  ,
, 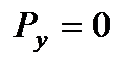 ,
, 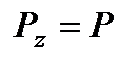 и, і
и, і 
Робота сили тяжіння дорівнює узятому взятому зі знаком плюс або мінус добуток модуля сили на вертикальне переміщення точки її прикладення. Робота позитивна, якщо початкова точка вища за кінцеву, і негативна, якщо початкова точка нижча за кінцевоїкінцеву.
Приклад 2. Робота сили пружності.

| Рисунок 3.4 |
 . Нехай точка М, на яку діє тільки сила пружності, переміщується з положення
. Нехай точка М, на яку діє тільки сила пружності, переміщується з положення  в положення
в положення  .(
.( ,
, 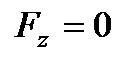 ).
).


| Рисунок 19.6 |
Робота сили пружності дорівнює площі фігури(трапеції) що розташована під кривою  .
.  Приклад 3. Робота и потужність пари сил.
Приклад 3. Робота и потужність пари сил.
Нехай пара сил,що додається, до обертається навколо фіксованої осі тіла. Елементарна робочої сили дорівнює  . Повна робота пари сил рівна дорівнює
. Повна робота пари сил рівна дорівнює 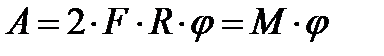 ,
,
де  – кут обертання тіла,;
– кут обертання тіла,;
 – момент пари сил.
– момент пари сил.
Потужність пари сил дорівнює
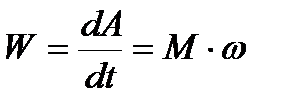 .
.
Кінетична енергія точки
Кінетична енергія матеріальної точки (або її жива сила) – половина добутку маси точки на квадрат її швидкості.

Теорема про зміну кінетичної енергії точки.
Теорема. Диференціал кінетичної енергії точки дорівнює елементарній роботі сили, що діє на точку.:

Доведення:. Основний закон динаміки  .
.
Помножимо ліву и і праву частину рівняння скалярна скалярно на  справа, отримуємо
справа, отримуємо  ,
,
де  – елементарна робота.
– елементарна робота.
 –диференціал від кінетичної енергії.;
–диференціал від кінетичної енергії.;
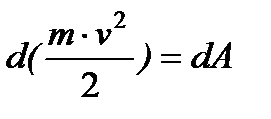 , що і й потрібно було довести.
, що і й потрібно було довести.
Теорема. Похідна за часом від кінетичної енергії точки дорівнює потужності, що підводиться до цієї точки.:

Теорема. Зміна кінетичної енергії точки на якому-небудь переміщенні дорівнює роботі сили, що діє на точку на цьому ж переміщенні.:
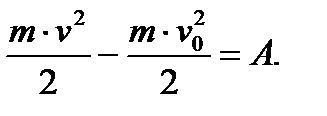
Принцип Даламбера для матеріальної точки
Рівняння руху матеріальної точки відносно інерційної системи відліку під дією прикладених активних сил і сил реакції зв’язків має вигляд:
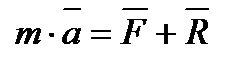 ,
,
 -– рівнодіюча рівнодійна активних сил,;
-– рівнодіюча рівнодійна активних сил,;  - рівнодіюча рівнодійна сил реакції зв'язків.
- рівнодіюча рівнодійна сил реакції зв'язків.
Силою інерції матеріальної точки називають добуток маси точки на вектор прискорення, взяте взятий із зворотним протилежним знаком, тобто
 .
.
Якщо використовувати поняття сили інерції, то основний закон динаміки набуває вигляду:  .
.
Принцип Даламбера. При русі матеріальної точки активні сили і сили реакції зв'язків разом із силою інерції точки утворюють рівноважну систему сил.
Принцип Даламбера називають ще методом кінетостатики. Завдання Задачі динаміки за допомогою цього методу зводяться до задач статики.
Лекція 20
Короткий зміст.: Динаміка невільної матеріальної точки. Відносний рух матеріальної точки. Окремі випадки.
Динаміка невільної матеріальної точки
Невільною матеріальною точкою називається точка, свобода руху якої обмежена.
Тіла, що обмежують свободу руху точки, називаються в’язями.
Нехай в’язь являє собою поверхню якого-небудь тіла, по якій рухається точка. Тоді координати точки мають задовольняти рівнянню рівняння цієї поверхні, яке називається рівнянням в’язі.

Якщо точка вимушена змушена рухатись рухатися по деякій лінії, то рівнянням в’язі є рівняння цієї линилінії.
 ,
,  .
.
Таким чином, рух невільної матеріальної точки залежить не тільки від прикладених до неї активних сил і початкових умов, але також від накладених в’язей. При цьому значення початкових параметрів мають задовольняти рівнянням в’язей.
В’язі бувають двосторонніми або утримуючими утримувальними і односторонніми або не утримуючимивальними.
В’язь називається двосторонньою, якщо, обмеження координати точки, що накладаються нею, виражаються в формі рівностей, що визначаючих визначають криві або поверхні в просторі, на яких має знаходитись знаходитися точка.

| Рисунок 20.1 |
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 602; Нарушение авторских прав?; Мы поможем в написании вашей работы!