Сглаживание уровней временного ряда

Средние по рядам динамики

1.Средний уровень ряда (`y):

а) для интервального ряда с равными интервалами рассчитывается по формуле средней арифметической простой:

б) для интервального ряда с неодинаковыми интервалами по формуле средней арифметической взвешенной:

где - уровни ряда динамики, сохранявшиеся без изменения в течении промежутка времени .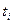

в) для моментного ряда с равными промежутками между моментами времени по формуле средней хронологической простой:

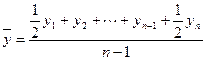
г) для моментного ряда с неравными промежутками:

;

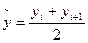
2. Средний абсолютный прирост (цепной)

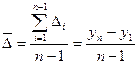
3. Средний коэффициент роста:

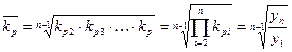
4.Срений темп роста: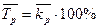

5.Срений темп прироста:

6.Средняя величина абсолютного значения 1% прироста:

Средние показатели используют при упрощённых приёмах прогнозирования.

Если тенденция временного ряда проявляется недостаточно четко (т.е. уровни ряда испытывают сильные колебания), то целесообразно предварительно произвести сглаживание уровней временного ряда.

Способы сглаживания:

1) Метод ступенчатой средней величины.

ti	yi

Найдем ступенчатую среднюю по кварталам.

у_ст1 = (2+4+3)/3 = 3

у_ст2 = (6+5+7)/3 = 6 и т.д.

2) Метод скользящей средней величины

Возьмем период 3 тогда получим следующие значения:

У_ск1 = (2+4+3)/3 = 3

У_ск2 = (4+3+6)/3 = 13/3 и т.д.

При этом мы теряем по 1 значению с начала и с конца временного ряда.

Если период скольжения четный, то необходимо произвести дополнительное центрирование полученных уровней для того, чтобы привязать их к исходным моментам времени. Для этого необходимо найти среднее между соседними значениями.

3) Экспоненциальное сглаживание

Смысл экспоненциальных средних в том, чтобы найти такие средние, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяется средняя.

Веса в экспоненциальных средних устанавливаются в виде коэффициентов α (0<α<1).

Веса по времени убывают экспоненциально, а сумма весов стремится к 1. В качестве весов используют следующий ряд:

α, α(1 - α), α(1 - α)²,…

Экспоненциальные средние рассчитываются по формуле:

Q_t = α*y_t + (1 – α)*Q_t-1

Q_t – экспоненциальная средняя (сглаженное значение уровня ряда на момент времени t)

α – вес текущего наблюдения.

y_t – фактический уровень временного ряда, соответствующий моменту времени t.

Q_t-1 – экспоненциальная средняя предыдущего периода.

Обычно α выбирают из диапазона 0.1<α<0.5. Чем ближе α к 1, тем меньше влияние на формирование средней оказывают предшествующие уровни ряда и наоборот. Уже при α = 0.9 сглаженные значения практически воспроизводят исходный ряд.

Дата добавления: 2014-12-16