Множественная корреляция. Формула Спирмена для корреляции связанных рангов

Формула Спирмена для корреляции связанных рангов

Оценка существенности коэффициента корреляции

При большом объеме выборки используется соотношение для коэффициента корреляции и его среднеквадратичной ошибки

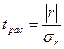
Если то следует говорить о существенности коэффициента корреляции.

При недостаточно большом объеме выборки величина ошибки .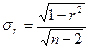

При этом .

j – номера связок по порядку для признака X,

A_j – число одинаковых рангов j-ой связки по X,

k – номера связок по Y,

B_k – число одинаковых рангов по Y в k-ой связке.

Целью регрессионного анализа в случае парной регрессии является предсказание значения результативного признака Y при определенном значении факторного признака X

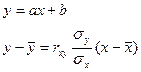
В случае множественной корреляции исследуется зависимость отклика системы от нескольких факторов

Изучение множественной корреляции начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости

Признак	y	x1	x2	…	xk
y		ry,x1	ry,x2	…	ry,xk
x1	rx1,y		rx1,x2	…	rx1,xk
x2	rx2,y	rx2,x1		…	rx2,xk
…	…	…	…	…	…
xk	rxk,y	rxk,x1	rxk,x2	…

При построении многофакторных моделей должно соблюдаться требование наименьшей коррелируемости включенных в модель признаков–факторов, т.е. отсутствия мультиколлинеарности. . При невыполнении хотя бы одного неравенства следует исключить факторный признак с менее тесной связью с Y.

Следует учитывать, что число факторов, включаемых в модель, должно быть в 5-6 раз меньше, чем число единиц, входящих в совокупность.

Совокупный коэффициент корреляции определяется следующим образом:

- определитель матрицы парных коэффициентов корреляции,

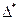- определитель матрицы, получаемый из матрицы парных коэффициентов корреляции путем вычеркивания 1 строки и 1 столбца,

- коэффициент детерминации. Он показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной регрессии. R не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе R к 1, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели верно отражают степень эффективности включенных в нее факторов.

Для сравнения роли различных факторов в формировании моделируемого показателя определяют α-коэффициенты (коэффициенты эластичности) и β-коэффициенты.

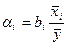показывает, на сколько процентов в среднем изменяется результативный признак Y c изменением фактора X_i на 1%. b_i – коэффициент регрессии при i-ом факторе.

β-коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный признак при изменении соответствующего фактора Х_i на величину его среднего квадратического отклонения:

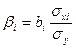
Рассмотрим простейшую модель линейной регрессии с 2-мя факторами X и Z

Y=b₀+b₁x+b₂z

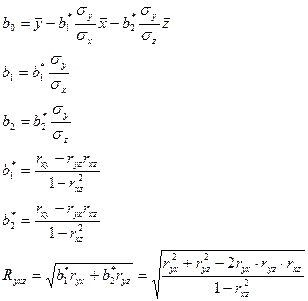
Дата добавления: 2014-12-16