
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Справочные материалы
|
|
|
|
Таблица простейших производных и интегралов
1.  ,
, 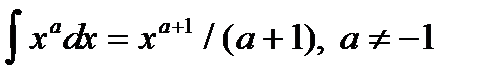 .
.
2. 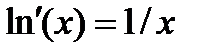 ,
, 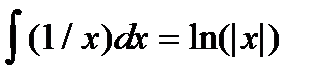 .
.
3.  ,
, 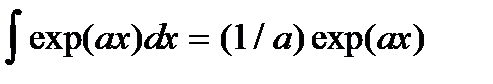 .
.
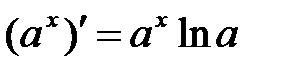

4. 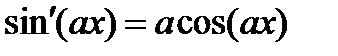 ,
, 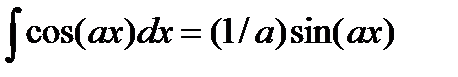 .
.
5.  ,
, 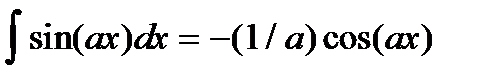 .
.
6.  ,
, 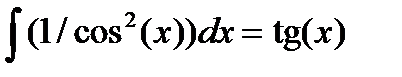 .
.
7.  ,
, 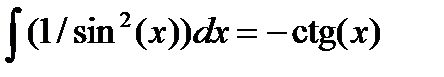 .
.
8.  ,
,  ,
,
 .
. 
9.  ,
,  ,
,
 .
. 
10.  ,
,  .
.
11.  ,
, 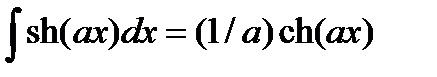 .
.
12. 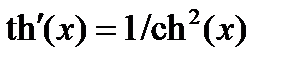 ,
,  .
.
13. 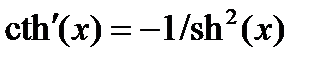 ,
, 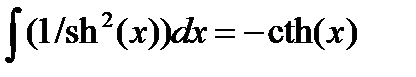 .
.
14. 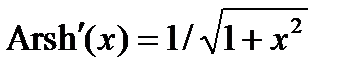 ,
,  .
.
 ,
, 
15. 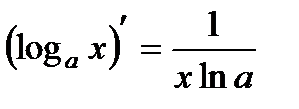

16. 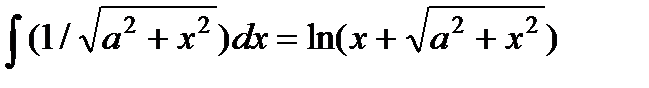
17. 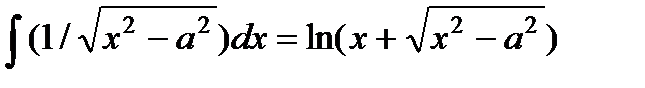
Расширенная таблица интегралов
1. 
2. 
3. 
4. 
5. 
6. 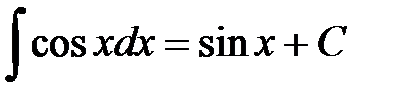
7. 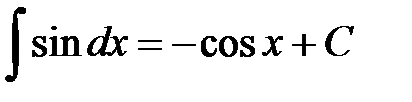
8. 
9. 
10. 
11. 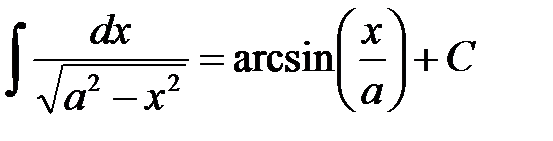
12. 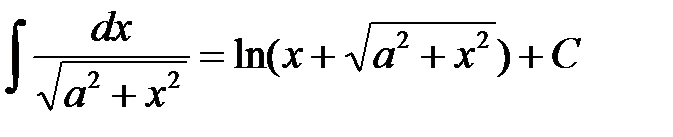
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 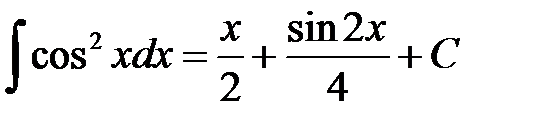
21. 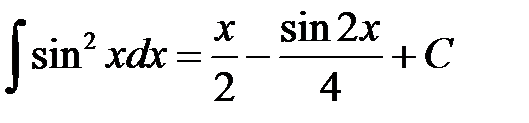
22. 
23. 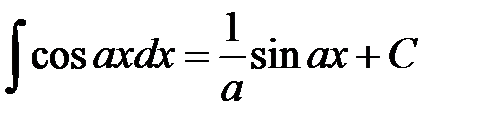
24. 
25. 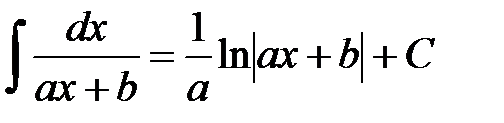
26. 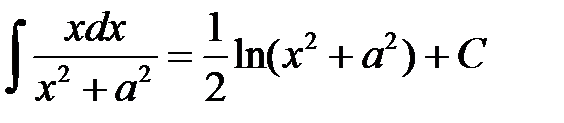
27. 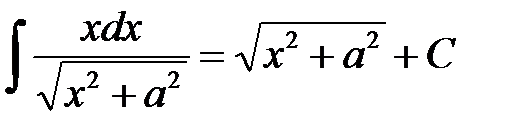
28. 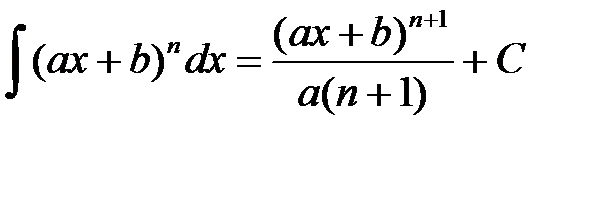
29. 
30. 
31. 
32. 
33. 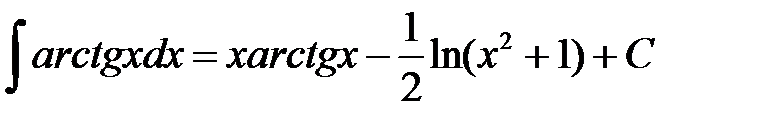
Занятия 5-7. Неопределенный интеграл. Основные методы интегрирования
1. Найти интегралы, используя линейность операции интегрирования: 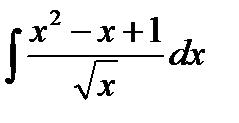
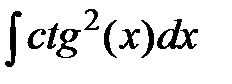

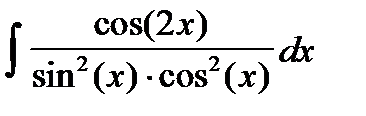
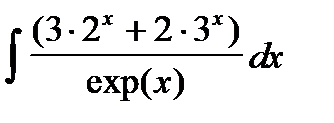

2. Найти интегралы, пользуясь подведением производной под знак дифференциала  :
:
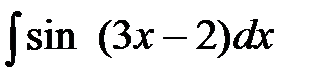
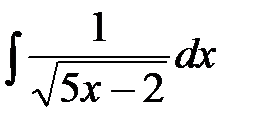
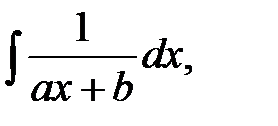

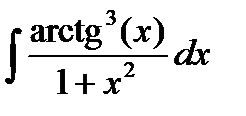
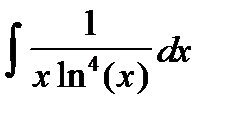
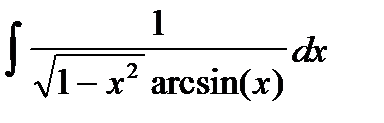
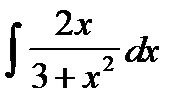


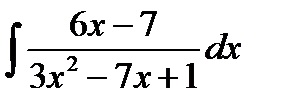
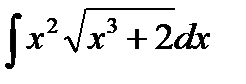
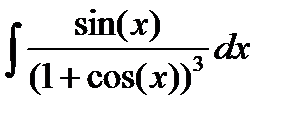





3. Найти интегралы, разбивая правильные дроби на сумму простейших дробей или выделяя целую часть и остаток для неправильных дробей:
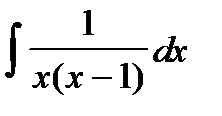

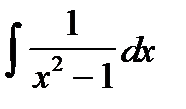

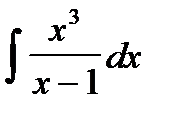
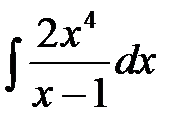
4. Найти интегралы при помощи замены с выделением полного квадрата (можно использовать формулы 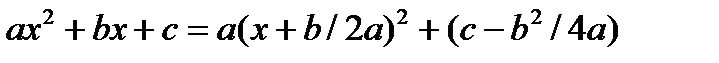 ,
,  ):
):
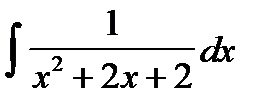


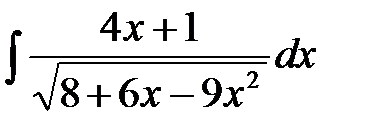

5. Найти интегралы, преобразуя подынтегральные функции указанными заменами переменных:

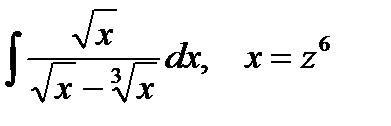
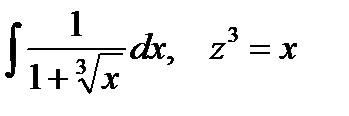
6. Найти интегралы, используя формулу интегрирования произведения (интегрирование по частям)  :
:

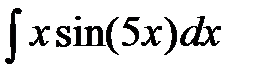

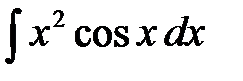
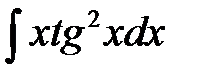
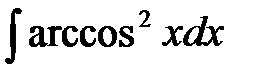
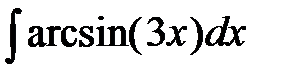

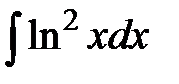
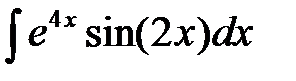


7. Найти интегралы, комбинируя рассмотренные выше элементарные приемы:
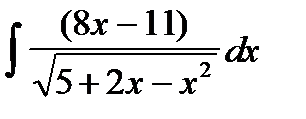
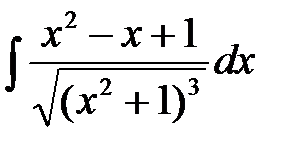



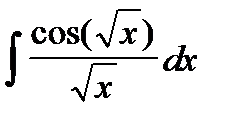


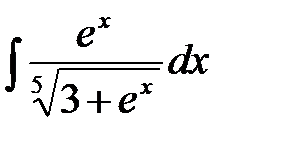
8. Проинтегрировать рациональные дроби:
 ,
, 


9. Проинтегрировать тригонометрические функции:

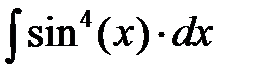



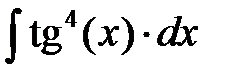

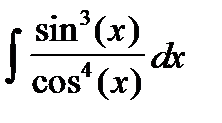
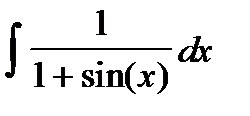
10. Проинтегрировать гиперболические функции:




11. Найти интегралы, избавляясь от квадратных корней при помощи тригонометрических или гиперболических подстановок:
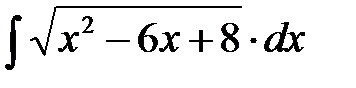
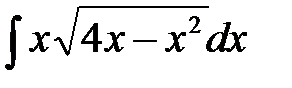
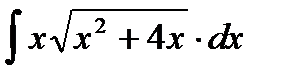

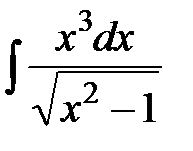
12. Найти интегралы, избавляясь от радикалов при помощи степенных подстановок:

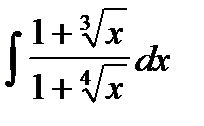

13. Найти интегралы, комбинируя различные приемы:


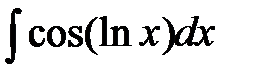
Занятие 8. Определенный интеграл.
1. Вычислить определенные интегралы, используя формулу Ньютона-Лейбница
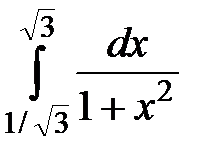 ,
,  ,
,  ,
, 
2. Вычислить, используя свойства определенного интеграла
 ,
, 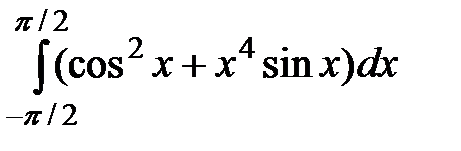 ,
, 
Занятие 9. Несобственные интегралы.
1.Вычислить несобственные интегралы или исследовать их на сходимость
 ,
,  ,
,  ,
,
 ,
, 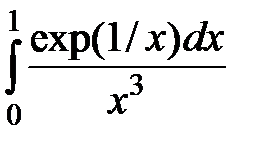
 ,
, 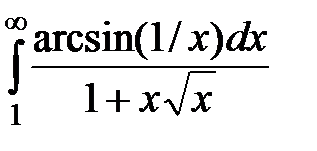
Занятия 10. Контрольная работа «Техника дифференцирования и интегрирования». Контрольная работа состоит из 5 задач:
1.Производная (сложная функция, арифметические операции)
2.Метод замены переменной в неопределенном интеграле
3. Метод интегрирования по частям
4. Интегрирование дробно-рациональных функций
5.Интегрирование иррациональных функций (метод подстановки)
Занятие 11. Числовой ряд. Признаки сходимости
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 526; Нарушение авторских прав?; Мы поможем в написании вашей работы!