Правило суми

Властивості відношень- рефлексивність-кожен елемент даної множини х перебуває у відношені R сам з собою. Симетричність-якщо елемент х перебуває у відношені R з елементом У то У перебуває у відношені з х. Транзитивність-якщо елемент х перебуває у відношені R з У, а У перебуває у відношені з Z,то це X R Z. Якщо відношення має властивості рефлексивності, симетричності, транзетивності, то його наз. ек’ювалентність,тобто воно розбиває множину х на класи екювалентності. Відношення на множині яке має властивості антирефлексивності, антисеметричності, транзитивності наз. відношення строгого порядку. Якщо відношення рефлексивне, антисиметричне і транзитивне то це відношення не строгого порядку.

Відношення на одній множині їх властивості.

Правило суми та добутку

правило суми: якщо деякий елемент А можна вибрати m способами, а елемент В — r способами (причому будь-який вибір елемента А відрізняється від вибору елемента В), то вибрати А або В можна m + r способами.

Приклад 1. В ящику знаходиться 7 білих і 4 чорних кульки. Тоді вибрати одну кульку: білу або чорну можна 7 + 4 = 11 способами. Зрозуміло, що правило суми можна розповсюдити на три і більше елементів.

правило добутку: якщо деякий елемент А можна вибрати m способами, а після кожного такого вибору інший елемент В можна вибрати (незалежно від вибору елемента А) — r способами, то пару об’єктів А і В можна вибрати mr способами.

Приклад 2. У шкільній їдальні є вибір з 3 перших і 5 других блюд. Тоді обід з першого і другого блюда можна обрати 3 ∙ 5 = 15 способами. Правило добутку розповсюджується на три і більше елементів.

Довільна підмножина множини А1´А2´...´Аn називається відношенням,

заданим або визначеним на множинах А1, А2,..., Аn. Загалом відношення означає який-небудь зв’язок між предметами або поняттями.

52. поняття про комбінаторні задачі. Правела суми та добутку

Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай, скінченної множинивідповідно до заданих правил.

У комбінаториці є декілька задач, які вирішуються послідовно одна за одною. Перша з них спочатку формулює вимоги до класу комбінаторних конфігурацій, які потрібно побудувати. Доводиться, що хоча б одна така конфігурація існує, попри те, що побудувати таку конфігурацію може бути досить непросто. Тому інколи буває достатньо теоретичного доведення її існування.

Після розв'язання першої задачі комбінаторики розв'язується не менш важлива друга — задача переліку комбінаторних об'єктів, які відповідають вихідним правилам їх побудови. Саме на розв'язання цієї задачі спрямовані сьогодні зусилля багатьох учених. Є досить багато задач, які так чи інакше стосуються цієї загальної задачі. Наприклад, до неї належить питання про кількість різних способів, якими можна розмістити групу студентів з 30 чоловік на 30 чи більше місцях, або про кількість способів проведення матчів з футболу між 10 різними командами?

Далі на основі отриманих розв'язків конкретних задач з переліку комбінаторних об'єктів розв'язується третя задача комбінаторики — це її побудова. Наприклад, потрібно не лише підрахувати кількість можливих варіантів розподілу 30 студентів на 30 місцях, а й побудувати всі ці розподіли або деякі з них у вигляді їх комбінаторних конфігурацій. Також може виникнути потреба побудувати таблицю матчів між 10 футбольними командами, а не тільки знати їх кількість.

Четверта і остання задача комбінаторики — це задача про пошук серед комбінаторних конфігурацій такої, яка б приводила деяку функцію до оптимуму. Це на сьогодні досить нелегка для розв'язання загальна задача. Вона містить задачі комбінаторної оптимізації, наприклад, задачу комівояжера, яка на сьогодні ще не має остаточного розв'язання.

В основі розв'язання багатьох задач комбінаторики лежать два простих правила — правило суми та правило добутку. Правило суми стверджує, що якщо є можливість вибрати елемент з деякої множини елементів А 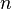способами, а елемент з множини В, яка не має спільних елементів з множиною А, — 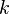способами, то вибрати елемент множини А або елемент множини В можна 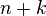способами.

Правило добутку використовується тоді, коли кожний елемент множини А може бути вибраний разом з елементом множини В. Відповідно до кожного способу вибору елемента множини А буде зіставлятися 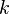способів вибору елемента множини В. Тоді загальна кількість способів сумісного вибору елементів множини А з елементами множини В, очевидно, дорівнюватиме .

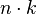Дата добавления: 2014-12-16