Числовые характеристики дискретных случайных величин

Случайные величины. Законы их распределения

Случайной величиной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее не известно, какое именно. Примеры случайных величин:

1) годовой удой от одной коровы в литрах;

2) число яиц, полученных от одной несушки за год;

3) число растений ржи на 1 м²;

4) глубина заделки семян при посеве.

Дискретной называется случайная величина, значения которой изолированы друг от друга, и их можно пронумеровать. При этом число значений может быть конечным или бесконечным.

Непрерывной называется случайная величина, значения которой сплошь заполняют некоторый интервал, конечный или бесконечный.

Законом распределения дискретной случайной величины X называется соответствие между возможными значениями случайной величины и вероятностями этих значений.

Закон распределения чаще всего записывают в виде таблицы из двух строк. В верхней строке перечисляются значения, которые принимает случайная величина, а в нижней - вероятности этих значений, т.е.

X	x1	х2	...	xn
P	p1	p2	…	pn

p_i = Р(Х = х_i) ≥ 0;i = 1,2... n.

Заметим, что всегда р₁ + р₂ +... + р_i = 1.

Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки М₁(x₁, p₁), М₂(х₂, р₂)... М_n(х_n, р_n) и соединяют их отрезками прямой. Полученную фигуру называют многоугольником распределения.

Математическим ожиданием дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности:

М(Х) = x₁p₁ + x₂p₂ + … + x_np_n =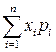

Математическое ожидание характеризует среднее значение случайной величины.

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

D(Х) = М(Х – М(Х))² или

D(Х) = 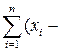М(х))² р,

Справедлива и другая формула: D(Х) = М(Х²) – М²(Х)

Дисперсия характеризует рассеяние возможных значений случайной величины вокруг своего математического ожидания, мерой такого рассеяния является среднее квадратическое отклонение, равное корню квадратному из дисперсии, т.е.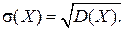

Дата добавления: 2014-12-16