
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Произведение матриц
|
|
|
|
Пусть 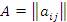 – m × l матрица и пусть
– m × l матрица и пусть 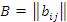 – l × n матрица.
– l × n матрица.
Тогда произведением AB называется матрица 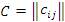 размера m × n, элементы
размера m × n, элементы 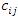 которой вычисляются по правилу умножения i -ой строки матрицы A на j -ый столбец матрицы B:
которой вычисляются по правилу умножения i -ой строки матрицы A на j -ый столбец матрицы B:
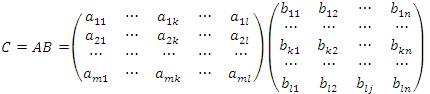 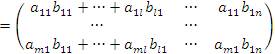
| (1а) | ||
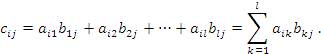
| (1б) |
Если обозначить строки матрицы A символами 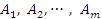 , а столбцы матрицы B – символами
, а столбцы матрицы B – символами 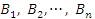 , то правило (1) матричного умножения можно представить в следующем блочном виде:
, то правило (1) матричного умножения можно представить в следующем блочном виде:
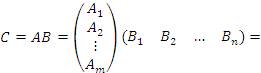 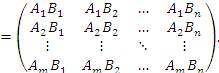
| (2) |
Таким образом, если матрица A содержит m строк, а матрица B содержит n -столбцов, то произведение AB представляет собой матрицу С размера m × n. Элемент 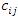 , стоящий в i -ой строке и j -ом столбце матрицы AB, вычисляется по правилу умножения строки на столбец: i -ая строка матрицы A умножается на j -ый столбец матрицы B.
, стоящий в i -ой строке и j -ом столбце матрицы AB, вычисляется по правилу умножения строки на столбец: i -ая строка матрицы A умножается на j -ый столбец матрицы B.
Операция матричного умножения определена только для матриц, удовлетворяющих определенным условиям:
- Произведение AB определено, если число столбцов матрицы A совпадает с числом строк матрицы B. (Другими словами, число элементов в строке матрицы A должно совпадать с числом элементов в столбце матрицы B.)
- Произведение BA определено, если число столбцов матрицы B совпадает с числом строк матрицы A.
Отметим, что в общем случае произведение матриц некоммутативно, то есть AB ≠ BA. Более того,
- Существование одного из произведений (AB или BA) не влечет за собой существование другого.
- Если определено каждое из таких произведений, то размеры матриц AB и BA не обязательно совпадают друг с другом. Например, результатом умножения матрицы A размера 1× n на матрицу B размера n ×1 является число (то есть матрица размера 1×1), тогда как произведение BA представляет собой квадратную матрицу n -го порядка.
- Если матрицы A и B являются квадратными маирицами n -го, то и их произведения AB и BA являются матрицами такого же порядка. Однако даже для таких матриц их произведения в одном и другом порядках равны только в некоторых частных случаях.
- Произведение нескольких матриц, расположенных в определенном порядке, однозначно определено, если число столбцов каждой матрицы равно числу строк соседней матрицы справа. В этом случае для нахождения произведения матриц можно использоать произвольный порядок расстановки скобок (см Свойства матричных операций).
Разность AB – BA произведений квадратных матриц одного и того же порядка называется коммутатором матриц.
Сумма AB + BA произведений квадратных матриц одного и того же порядка называется антикоммутатором матриц.
Символическая запись 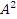 означает произведение двух одинаковых квадратных матриц:
означает произведение двух одинаковых квадратных матриц: 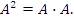
Аналогичным образом определяются другие целые положительные степени квадратной матрицы:
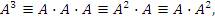 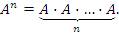 . .
| (3) |
Правило (1) матричного умножения сохраняет свой вид и в том случае, когда элементами матриц A и B являются другие матрицы. Пусть, например, матрицы A и B представлены в виде
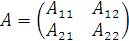
| (4) |
где Ai j и Bi j – некоторые матрицы, размеры которых таковы, что соответствующие матричные произведения определены.
Тогда

| (5) | ||||
Пример 1. Найти коммутатор матриц 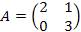 и и 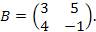 Решение: Решение:
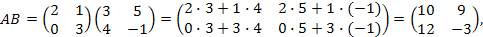 и
и
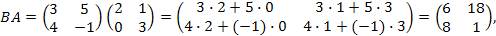 Тогда
Тогда
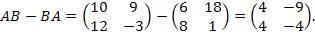
| |||||
***
Пример 2. Найти A 2010, если 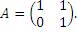 Решение: Решение:
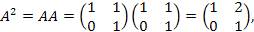 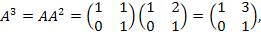 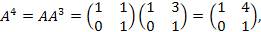 … … 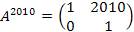
|
***
Пример 3. Пусть  - матрица второго порядка с произвольными элементами. Покажем непосредственным вычислением, что матрица вида - матрица второго порядка с произвольными элементами. Покажем непосредственным вычислением, что матрица вида 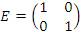 играет в матричной алгебре роль единицы. Действительно, играет в матричной алгебре роль единицы. Действительно,
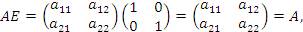 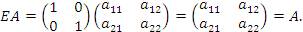
|
***
Пример 4. Аналогично, матрица  не изменяется при умножении слева или справа на матрицу не изменяется при умножении слева или справа на матрицу 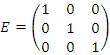 : :

|
***
Пример 5. В условиях Примера 1 найти антикоммутатор матриц A и B. Решение:
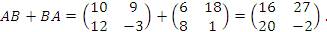
|
***
Пример 6. Пусть 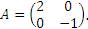 Показать, что Показать, что 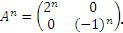 Решение: Решение:
 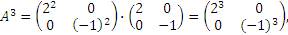 ... ... 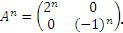
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 988; Нарушение авторских прав?; Мы поможем в написании вашей работы!