Диагональные матрицы

В квадратной матрице 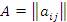элементы 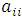(i = 1, 2,..., n) образуют главную диагональ и называются диагональными элементами. Главная диагональ проходит из левого верхнего угла матрицы в ее правый нижний угол.

(1)

Совокупность элементов, расположенных на диагонали, проходящей из правого верхнего угла в левый нижний угол, называется побочной диагональю.

Матрица 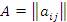, все внедиагональные элементы которой равны нулю, называется диагональной. Другими словами, элементы диагональной матрицы удовлетворяют условиям

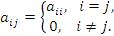
(2)

Для записи подобных выражений удобно использовать дельта-символ Кронекера, определяемый формулой

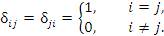
(3)

Очевидно, что дельта-символ симметричен относительно перестановки индексов:

δ i j = δ j i.

(4)

Другое важное свойство дельта-символа δ _{i j} заключается в том, что он снимает суммирование в выражениях вида

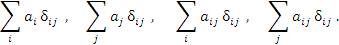
(5)

В частности,

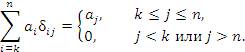
(6)

В этих обозначениях формула (2) принимает вид

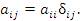
(7)

Очевидно, что при умножении прямоугольной матрицы A справа на диагональную матрицу с диагональными элементами λ₁, λ₁,..., λ _n первый столбец матрицы A умножается на число λ₁, второй - на число λ₂ и так далее.
При умножении матрицы A слева на такую диагональную матрицу каждая строка матрицы A умножается на соответствующее число λ _i.

Диагональная квадратная матрица с равными диагональными элементами называется скалярной.

Пример 1. Доказать, что произведение диагональных матриц есть диагональная матрица. Доказательство: Пусть 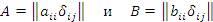– произвольные диагональные матрицы n -го порядка. Рассмотрим i, j -ый элемент матричного произведения AB: . Выражение в правой части этого равенства представляет собой матричный элемент диагональной матрицы.

***

Пример 2. Доказать, что коммутатор диагональных матриц равен нулю. Доказательство: Пусть 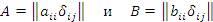– произвольные диагональные матрицы n -го порядка. Рассмотрим i, j -ый элемент матричного произведения BA: 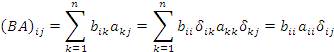. Учитывая, что произведение диагональных матриц есть диагональная матрица (см Пример 1), заключаем, что произведение диагональных матриц коммутативно: AB = BA.

***

Пример 3. Сумма 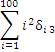содержит только одно ненулевое слагаемое, поскольку δ _{i 3} = 1 при i = 3 и δ _{i 3} = 0 для всех других значений i. Следовательно,

***

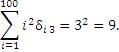
Пример 4. Сумма содержит только нулевые слагаемые, поскольку δ _{i 120} = 0 для всех 1 ≤ i ≤ 100. Следовательно,

***

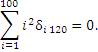
Пример 5.

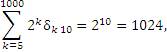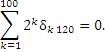
Дата добавления: 2014-12-16