Следствия

Теоремы о транспозициях и перестановках

Теорема 1. Любая транспозиция изменяет четность перестановки.

Доказательство.
Утверждение теоремы представляется вполне очевидным в случае транспозиции соседних элементов, поскольку взаимная перестановка элементов i_j и i_{j +1} приводит к появлению или исчезновению инверсии между ними.

Транспозицию элементов i_j и i_j+k можно рассматривать как результат k последовательных транспозиций элемента i_j с соседними элементами, расположенными справа от i_j, и последующих k - 1 транспозиций элемента i_j+k с соседними элементами, расположенными слева от i_j+k:

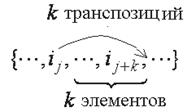
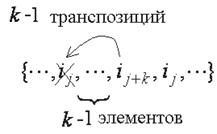
Полное число транспозиций k + (k - 1) = 2 k - 1 является нечетным числом, что означает изменение четности перестановки.

1. Четная перестановка возникает в результате четного числа транспозиций элементов множества S = {1, 2,..., n }.
2. Нечетная перестановка возникает в результате нечетного числа транспозиций элементов множества S.

Теорема 2. Существует n! различных перестановок множества S = {1, 2,..., n }.

Доказательство.
В произвольной перестановке множества S в первой позиции может располагаться любое из первых n натуральных чисел.
Для каждого из этих n вариантов во вторую позицию можно поместить любое из оставшихся (n -1) чисел, в третью – любое из оставшихся (n - 2) чисел и так далее. Последняя n -ая позиция может быть замещена единственным оставшимся элементом.
Таким образом, общее число различных перестановок множества S равно n (n – 1)(n – 2)...1 = n!.

Примеры:

1. Множество S = {1, 2, 3} содержит три элемента, и поэтому число различных перестановок этого множества равно 3! = 6:

{1, 2, 3}, {1, 3, 2}, {2, 3, 1}, {2, 1, 3}, {3, 1, 2} {3, 2, 1}.

***

1. Показать, что перестановка P = {2, 3, 1} является четной. Решение. Элементы 2 и 1 образуют инверсию, поскольку число 2 расположено слева от меньшего числа 1. Элементы 3 и 1 образуют инверсию, поскольку число 3 расположено слева от меньшего числа 1.

Таким образом, перестановка P содержит четное число инверсий. Другое решение. Перестановка P является четной, поскольку представляет собой результат четного числа последовательных транспозиций элементов множества S = {1, 2, 3}: {1, 2, 3} ⇒ {1, 3, 2} ⇒ {2, 3, 1}.

***

1. Показать, что перестановка Q = {3, 1, 2} является четной. Решение. Достаточно показать, что перестановка Q содержит четное число инверсий. Элементы 3 и 1 образуют инверсию, поскольку число 3 расположено слева от меньшего числа 1. Элементы 3 и 2 образуют инверсию, поскольку число 3 расположено слева от меньшего числа 2. Элементы 1 и 2 не образуют инверсию.

Таким образом, перестановка Q содержит четное число инверсий.

Дата добавления: 2014-12-16