Матрицы Паули

Матрицы Паули σ _k (k = 1, 2, 3) определяются уравнениями

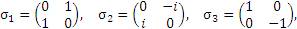
(1)

и используются для описания спиновых состояний электронов. (Здесь i – мнимая единица.)

Очевидно, что матрицы Паули являются эрмитовыми::

(2)

Квадрат каждой из матриц Паули равен единичной матрице:

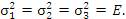
(3)

Матрицы Паули обладают свойством антикоммутативности:

(4)

где – дельта-символ Кронекера (j, k = 1,2,3).

Другие непосредственно проверяемые свойства матриц Паули:

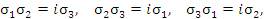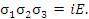
(5)

Матрицы вида e^A

Для описания эволюции состояния квантовой системы важную роль играют матрицы вида 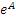, где A – некоторая квадратная матрица (конечного или бесконечного порядка).

Методами математического анализа устанавливается справедливость разложения функции 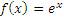по формуле Тейлора:

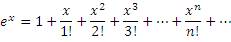
(1)

где число e представляет собой основание натуральных логарифмов:

e = 2.7182818284590452353602874...

(2)

Тогда выражение вида

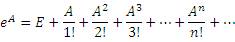
(3)

можно рассматривать в качестве определения марицы .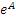

Например, если

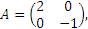
(4)

то нетрудно показать (см Пример 6), что

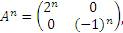
(5)

где n – натуральное число.
Тогда

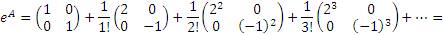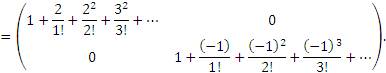
(6)

Учитывая равенство (1), заключаем, что матрица 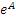может быть представлена в виде

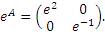
(7)

Заметим, что нахождение матрицы 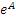сводится к суммированию конечного числа матриц, если существует такое целое положительное число n, что Aⁿ = 0. Такое условие выполняется, например, для треугольных матриц с нулевыми диагональными элементами.
В частности, в случае матрицы A третьего порядка вида

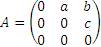
(8)

уже ее третья степень представляет собой нуль-матрицу:

,

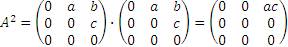(9)

Следовательно,

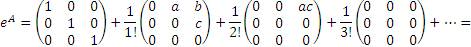
(10)

Пример 1.
Для данной матрицы

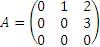
найти матрицу .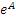

Дата добавления: 2014-12-16