Матрица масштабирования

Если в единичной матрице заменить диагональные элементы произвольными ненулевыми числами, то полученная матрица называется матрицей масштабирования.
Иначе говоря, любая диагональная матрица с ненулевыми диагональными элементами является матрицей масштабирования.

Если матрицы масштабирования получена из единичной матрицы E умножением одной из ее строк (или столбца) на ненулевое число λ, то такая матрица называется элементарной матрицей масштабирования.

Легко проверяются следующие свойства элементарной матрицы масштабирования.

1. Умножение слева элементарной матрицы масштабирования на прямоугольную матрицу A приводит к умножению соответствующей строки матрицы A на число λ.
2. Умножение справа элементарной матрицы масштабирования на прямоугольную матрицу A приводит к умножению соответствующего столбца матрицы A на число λ.

Пусть, например, второй строкой матрицы масштабирования является строка вида (0, λ, 0, 0,..., 0). Тогда результатом умножения этой строки на столбцы прямоугольной матрицы A = || a_{i j} || является строка (λ a ₂₁ λ a ₂₂ λ a ₂₃...).

Терема 1. Произведение матриц масштабирования одного и того же порядка есть матрица масштабирования.

Терема 2. Матрица масштабирования n -го порядка может быть представлена в виде произведения (n - 1) элементарных матриц масштабирования.

Доказательство этих утверждений предоставляется читателю.

Примеры матриц масштабирования.

Элементарные матрицы масштабирования:

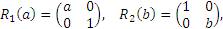
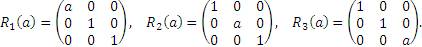
Матрицы масштабирования:

Дата добавления: 2014-12-16