Основные законы механики

Любое множество взаимодействующих материальных точек называется механической системой.

Модели материальных тел

Теоретическая механика является естественной наукой, опирающейся на результаты опыта и наблюдений и использующей математический аппарат при анализе результатов этих наблюдений. Изучая какое-либо явление, мы не можем охватить его во всем многообразии. Отвлекаясь при изучении механического движения материальных тел от всего частного, менее существенного, второстепенного и учитывая только те свойства, которые в данной задаче являются определяющими, мы приходим к рассмотрению различных моделей материальных тел, представляющих собой ту или иную степень абстракции.

Дадим определения основных моделей, используемых в теоретической механике.

1. Материальное тело, размерами и различием в движении отдельных точек которого можно пренебречь в рамках рассматриваемой задачи, называется материальной точкой.

3. Если расстояние между любыми двумя точками тела не изменяется при любых механических взаимодействиях, то такое тело называется абсолютно твёрдым.

Правильный выбор модели во многом определяет успех решения поставленной задачи. Заметим, что среди перечисленных моделей наиболее общей, можно сказать всеобъемлющей, является модель механической системы. Следовательно, и все закономерности движения, установленные на основе этой модели, являются наиболее общими. Всякая попытка конкретизации свойств механической системы, учёт особенностей той или иной среды (жидкости, газа, упругого тела и т.д.) приводит, как правило, к столь большому росту объёма информации, что возникает необходимость специализации, возникают новые науки (теория упругости, гидродинамика. аэродинамика и т.д.).

Теоретическая механика относится к числу так называемых аксиоматических наук. В ее основе лежит система исходных положений – аксиом, принимаемых без доказательства, но проверенных не только прямыми экспериментами, но и многовековой практикой человечества. Справедливость следствий, логически вытекающих из этих основных положений, также подтверждается экспериментальными данными.

Аксиома 1

Существует система отсчёта, по отношению к которой материальная точка находится в покое или движется равномерно и прямолинейно, если на неё не действуют силы.

Такая система отсчёта называется инерциальной, иногда ее условно называют неподвижной.

Аксиома 2

В инерциальной системе отсчёта произведение массы материальной точки на вектор ее ускорения равно приложенной к точке силе:

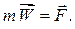
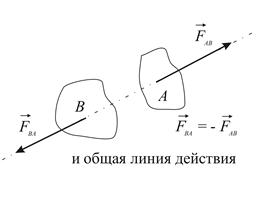
Рис.1.2

Здесь 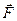– сила, действующая на материальную точку; 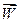– ее ускорение; 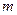– масса материальной точки, которая, как видно, является мерой ее инертности.

В самом деле, одна и та же сила сообщает точкам тем большее по модулю ускорение, чем меньше их масса:

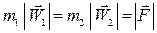
и следовательно, если 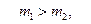то

.

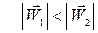Дата добавления: 2014-12-16