Ускорение точки

Быстроту изменения вектора скорости характеризует ускорение точки. Пусть в момент времени точка находится в положении и имеет скорость , а в момент , переходит в положение 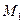и имеет скорость (Рис.1.5).

Ускорением точки называется предел отношения приращения вектора скорости к промежутку времени, за который это приращение произошло, при величине промежутка времени, стремящейся к нулю:

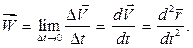(1.6)

Таким образом,

ускорение точки равно первой производной по времени от вектора скорости точки или второй производной по времени от радиуса–вектора точки.

Рис.1.5

Если траектория плоская кривая, то вектор ускорения лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория пространственная кривая, то при предельном переходе 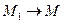плоскость, содержащая 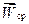(на чертеже заштрихована), будет поворачиваться вокруг вектора и в пределе займет положение, которое называется соприкасающейся плоскостью к траектории в точке .

Таким образом,

вектор ускорения точки лежит в соприкасающейся к траектории в данной точке плоскости, причем направлен в сторону вогнутости траектории.

Пусть движение точки задано в координатной форме, т.е. уравнениями (1.1). Тогда

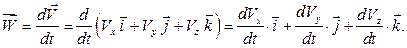
Таким образом,

проекции вектора ускорения на координатные оси равны первым производным по времени от соответствующих проекций вектора скорости или, учитывая равенства (1.5), вторым производным по времени от соответствующих координат точки:

(1.7)

Дата добавления: 2014-12-16