Аксиома 3. Не изменяя действия системы сил на тело, к ней можно добавлять или от нее отбрасывать уравновешенную систему сил

Не изменяя действия системы сил на тело, к ней можно добавлять или от нее отбрасывать уравновешенную систему сил

Аксиома 2

Если система сил эквивалентна одной силе, то эта сила называется равнодействующей системы сил

Определение 3

Система сил, под действием которой свободное твердое тело может оставаться в покое по отношению к инерциальной системе отсчета, называется уравновешенной или эквивалентной нулю

Определение 2

Определение 1

Две системы сил называются эквивалентными, если приложение каждой из них к одному и тому же покоящемуся свободному твёрдому телу приводят к одному и тому же движению

В основе действий над силами лежит система простейших правил, которые обычно называют аксиомами статики.

Аксиома 1

Две силы, приложенные в одной точке тела, эквивалентны одной силе (имеют равнодействующую), приложенной в той же точке и равной геометрической сумме этих сил (Рис.3.1)

По существу, приведенное здесь утверждение содержится в сформулированном ранее принципе независимости действия сил.

Рис.2.1		Рис.2.2

Система двух сил, приложенная к абсолютно твердому телу, уравновешена (эквивалентна нулю) тогда и только тогда, когда эти силы равны по модулю и действуют по одной прямой в противоположные стороны (Рис.3.2).

Сформулированные аксиомы позволяют рассматривать систему сил, приложенную к абсолютно твердому телу, как систему скользящих векторов. В самом деле, аксиома 1 позволяет рассматривать силу как вектор. Покажем, что это вектор скользящий.

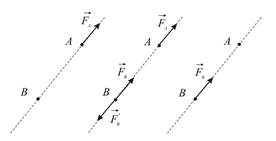
Рис.2.3

Пусть в точке 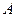абсолютно твердого тела приложена сила . Выберем на линии действия силы любую точку 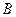, в которой приложим уравновешенную систему сил (Рис.3.3)

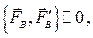причём

Силы и 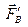образуют уравновешенную систему сил и, следовательно, могут быть отброшены. Таким образом,

не изменяя действия силы на абсолютно твердое тело, силу можно переносить в любую точку ее линии действия.

Дата добавления: 2014-12-16