
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коломна 2013
|
|
|
|
Тема 2. Государство и право Древней Руси.
Связь истории отечественного государства и права с другими юридическими дисциплинами.

План:
1. Догосударственный быт восточных славян
2. Рождение (генезис) Древнерусского государства
3. Общественный строй Киевской Руси
4. Государственный строй
5. Форма Древнерусского государства
6. Основные черты права Древней Руси
СОДЕРЖАНИЕ
ТЕМА 1................................................................................. Системы счисления... 3
Методические указания.. 3
Задача 1. Выполнить указанные в таблице задания.. 7
Варианты.. 7
Пример выполнения. 8
Задача 2. В какой системе счисления справедливо заданное равенство?.. 9
Варианты.. 9
Пример выполнения. 9
Задача 3. Найти основание x системы счисления, для которой выполняется равенство.. 9
Варианты.. 9
Пример выполнения. 9
Задача 4. Вычислить значение заданного выражения в десятичной системе счисления. Перевести каждое число в двоичную систему счисления (с точностью до 4 разрядов после запятой). Выполнить все действия в двоичной системе счисления. Результат перевести в десятичную систему счисления. Определить погрешность вычисления как разность между результатами первого и последнего действий 9
Варианты.. 9
Пример выполнения. 10
Задача 5. Для заданного десятичного числа выполнить следующие преобразования систем счисления: 10’8’10’16’10; 8’16.. 11
Варианты.. 11
Пример выполнения. 11
ТЕМА 2........................................................... Представление информации... 13
Методические указания.. 13
Ячейки памяти и машинные двоичные коды.. 13
Представление целых чисел без знака.. 14
Представление целых чисел со знаком.. 14
Представление вещественных чисел в типе Single. 15
Задача 6.Два числа X1 и X2 хранятся в формате 1 байт со знаком. Заданы их шестнадцатеричные значения. Чему равны их десятичные значения?.. 16
Варианты.. 16
Пример выполнения. 16
Задача 7.Проинтерпретировать 16 разрядов памяти компьютера в соответствии со следующими типами языка Паскаль: Byte, Shortint, Char, Word, Integer. 17
Варианты.. 17
Пример выполнения. 17
Задача 8.Переменная А имеет тип Single языка Паскаль. Задано представление значения А в шестнадцатеричной системе счисления. Чему равно десятичное значение числа A?.. 18
Варианты.. 18
Пример выполнения. 19
ТЕМА 3....................................................................... Основы алгебры логики... 20
Методические указания.. 20
Задача 9.Вычислить значение логического выражения на заданном наборе логических переменных. 20
Варианты.. 20
Пример выполнения. 21
Задача 10.Проверить справедливость равенства, используя законы алгебры логики. 21
Варианты.. 21
Пример выполнения. 21
Задача 11.Упростить логическое выражение, используя законы алгебры логики 22
Варианты.. 22
Пример выполнения. 22
Варианты заданий К КОНТРОЛЬНОЙ РАБОТЕ.. 23
Литература... 26
ПРИЛОЖЕНИЕ кодировка символов.. 26
ТЕМА 1. Системы счисления
Методические указания
Система счисления – это совокупность приёмов и правил представления чисел посредством числовых символов (цифр).
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (вклад в значение числа) не зависит от её позиции в числе. Например, в римской системе в числе ХХI (двадцать один) вес цифры Х в любой позиции равен десяти.
В позиционных системах вес цифры определяется её позицией в числе. Например, в десятичном числе 525,5 первая пятёрка означает 5 сотен, вторая – 5 единиц, третья – 5 десятых долей единицы. Запись числа 525,5 есть сокращённая запись суммы
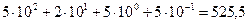 .
.
Основание позиционной системы счисления – это количество цифр, используемых для представления чисел в этой системе.
В системе счисления с основанием р любое число
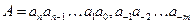
может быть представлено в виде суммы
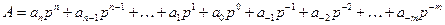 , (1)
, (1)
где 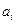 – цифры i -х разрядов числа;
– цифры i -х разрядов числа;
i – номера разрядов в числе, i = – m, – m+ 1, … – 1, 0, 1, 2, …, n –1, n;
р – основание системы счисления.
Разряды в числе нумеруются как 0, 1, 2, … справа налево от запятой в целой части и как –1, –2, … слева направо от запятой, отделяющей целую часть от дробной, например:
| Номера разрядов 3210–1 –2 –3 |
| 1520,041 |
Двоичная система счисления. Основание системы счисления равно 2. Для записи чисел используются две цифры 0 и 1. Двоичная система счисления используется для представления информации в памяти компьютера по следующим причинам: 1) простота реализации и надёжность работы устройств, имеющих два устойчивых состояния; 2) простота двоичной арифметики; 3) возможность использования одних и тех же устройств для реализации арифметических и логических операций, связанная со схожестью правил булевой алгебры и двоичной арифметики.
Правила выполнения арифметических операций в двоичной системе счисления:
| Сложение | Умножение | Вычитание | ||
| 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 | 0 ´ 0 = 0 0 ´ 1 = 0 1 ´ 0 = 0 1 ´ 1 = 1 | 0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 |
Пример 1. Выполнение арифметических операций в двоичной системе счисления:
| .2.2 | ´ | 101,101 | |||
| + | 101,1010 | – | 10111,1010 | ||
| 1100,1011 | 1100,1001 | + | |||
| 10010,0101 | 1011,0001 | ||||
| Переносы | 11 11 1 | 1000,0111 | |||
| Переносы |
При вычитании двоичных чисел используется известный в десятичной системе счисления приём занимания 1 из ближайшего слева (старшего) не равного нулю разряда (заём 1 из какой-либо цифры отмечается точкой над этой цифрой). Причём, если в десятичной системе счисления над цифрой разряда, для которого выполнялся заём, записывается число 10, то для двоичной системы счисления – число 2 (в общем случае – основание системы счисления, в которой выполняется вычитание). Это определяется свойством: основание системы счисления показывает, во сколько раз вес текущего разряда больше веса предыдущего разряда (с меньшим номером).
Восьмеричная система счисления. Основание системы счисления равно 8. Для записи чисел используются восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Прибавление единицы к старшей цифре 7 даёт первое двузначное число 10, т. е. 78 + 18 = 108.
Пример 2. Выполнение арифметических операций в восьмеричной системе счисления:
| . 8.8 | |||
| + | 125,71 | – | 572,75 |
| 16,24 | 124,56 | ||
| 144,15 | 446,17 | ||
| Переносы |
При сложении восьмеричных чисел в каждом разряде складываются две цифры, и если их сумма меньше восьми, то результат записывается в соответствующий разряд суммы. Если сумма цифр больше восьми, то из неё вычитается восемь, разность записывается в текущий разряд суммы, а единица переноса прибавляется к соседнему старшему разряду суммы.
При вычитании восьмеричных чисел используется приём занимания 1 из ближайшего слева не равного нулю разряда. Над цифрой разряда, для которого выполнялся заём, записывается число 8.
Шестнадцатеричная система счисления. Основание системы счисления равно 16. Для записи чисел используются шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F. Прибавление единицы к старшей цифре F даёт первое двузначное число 10, т. е. F16 + 116 = 1016.
Пример 3. Сложение и вычитание в шестнадцатеричной системе счисления:
| .16.16 | |||
| + | 1А5,В1 | – | 5F1,C5 |
| 1С,24 | 124,56 | ||
| 1C1,D5 | 4CD,6F | ||
| Переносы |
При сложении шестнадцатеричных чисел в каждом разряде складываются две цифры, и если их сумма меньше шестнадцати, то результат записывается в соответствующий разряд суммы. Если сумма цифр больше шестнадцати, то из неё вычитается шестнадцать, разность записывается в текущий разряд суммы, а единица переноса прибавляется к соседнему старшему разряду суммы.
При вычитании шестнадцатеричных чисел используется тот же приём занимания 1 из ближайшего слева (старшего) не равного нулю разряда. Над цифрой разряда, для которого выполнялся заём, записывается число 16.
Запись чисел в системах счисления с основаниями 10, 2, 8, 16
| B | |||||||||||
| C | |||||||||||
| D | |||||||||||
| E | |||||||||||
| F | 1A | ||||||||||
| 1B | |||||||||||
| 1C | |||||||||||
| 1D | |||||||||||
| 1E | |||||||||||
| 1F | |||||||||||
| A |
Перевод из десятичной системы счисления в систему счисления с основанием р.
1. Перевод целых чисел. Исходное десятичное число делится на основание той системы счисления, в которую переводим (р), нацело с записью целого частного и остатка от деления. Каждое полученное целое частное вновь делится на р до тех пор, пока частное от деления не станет равным нулю. Остатки от деления, записанные в порядке, обратном их получению, представляют искомое р -ичное число.
2. Перевод дробных чисел. Цифры десятичной дроби умножаются на основание той системы счисления, в которую переводим (р), с раздельной записью целой и дробной частей произведения. Дробные части произведений вновь умножаются на р по тому же правилу до тех пор, пока дробная часть очередного произведения не станет равной 0, либо пока не будет вычислено заданное количество дробных р -ичных цифр. Целые части произведений, записанные в порядке их получения, представляют цифры искомой р -ичной дроби.
Пример 4. Перевод чисел из десятичной системы счисления в двоичную:
| Перевод числа 11 | Перевод числа 0,7 с точностью до четырёх дробных цифр | |||
| Частные | Остатки | Целые части | Дробные части | |
| от деления на 2 | от умножения дробных частей на 2 | |||
| 0, | ||||
| 1 | ¯ 1 | |||
| 1 | ¯ 0 | |||
| 0 | ¯ 1 | |||
| 1 | ¯ 1 | |||
Получаем: 
| Получаем: 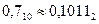
|
Пример 5. Перевод чисел из десятичной системы счисления в восьмеричную:
| Перевод числа 41 | Перевод числа 0,4 с точностью до двух дробных цифр | |||
| Частные | Остатки | Целые части | Дробные части | |
| от деления на 8 | от умножения дробных частей на 8 | |||
| 0, | ||||
| 1 | ¯ 3 | |||
| 5 | ¯ 1 | |||
Получаем: 
| Получаем: 
|
Пример 6. Перевод чисел из десятичной системы счисления в шестнадцатеричную:
| Перевод числа 75 | Перевод числа 0,9 с точностью до двух дробных цифр | |||
| Частные | Остатки | Целые части | Дробные части | |
| от деления на 16 | от умножения дробных частей на 16 | |||
| 0, | ||||
| 11 = В | ¯ Е Ü 14 | |||
| 4 | ¯ 6 | |||
Получаем: 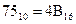
| Получаем: 
|
Перевод чисел из системы счисления с основанием р в десятичную систему счисления. Перевод р -ичного числа в десятичную систему счисления выполняется по формуле (1), при этом основание р и цифры числа записываются в десятичной системе счисления и все действия выполняются по правилам десятичной арифметики.
Пример 7. Переведём двоичное число 1010,011 в десятичную систему счисления. Для этого пронумеруем разряды в числе и запишем его по формуле (1):

Обратите внимание, что здесь выполнены переводы чисел, полученных в примере 4. Сравните результаты. Целое число из десятичной системы счисления было переведено точно, а дробное – приближённо. Последнее связано с тем, что при переводе дробного числа мы ограничились заданным количеством дробных цифр, а остальные отбросили, допустив тем самым погрешность перевода.
Пример 8. Переведём восьмеричное число  (числа из примера 5) в десятичную систему счисления:
(числа из примера 5) в десятичную систему счисления:
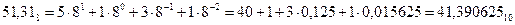 .
.
Пример 9. Переведём шестнадцатеричное число 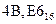 (числа из примера 6) в десятичную систему счисления:
(числа из примера 6) в десятичную систему счисления:
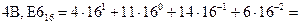
 .
.
Целые положительные и отрицательные степени чисел 2, 8 и 16
| 20 | 80 | 160 | 2–1 | 0,5 | |||||||
| 21 | 29 | 83 | 2–2 | 0,25 | |||||||
| 22 | 210 | 2–3 | 8–1 | 0,125 | |||||||
| 23 | 81 | 211 | 2–4 | 16–1 | 0,0625 | ||||||
| 24 | 161 | 212 | 84 | 163 | 2–5 | 0,03125 | |||||
| 25 | 213 | 2–6 | 8–2 | 0,015625 | |||||||
| 26 | 82 | 214 | 2–7 | 0,0078125 | |||||||
| 27 | 215 | 85 | 2–8 | 16–2 | 0,00390625 | ||||||
| 28 | 162 | 216 | 164 | 2–9 | 8–3 | 0,001953125 |
Перевод из восьмеричной системы счисления в двоичную. Поскольку  , то каждая восьмеричная цифра эквивалентна группе из трёх двоичных цифр (триаде):
, то каждая восьмеричная цифра эквивалентна группе из трёх двоичных цифр (триаде):
| Восьмеричная цифра | ||||||||
| Двоичная триада |
Для перевода из восьмеричной системы счисления в двоичную каждая цифра исходного восьмеричного числа заменяется соответствующей ей двоичной триадой, например:
| 2, | 28 | =11110010,012 | При записи результирующего двоичного числа незначащие нули можно отбросить. | ||
| ¯ | ¯ | ¯ | ¯ | ||
| 0112 | 1102 | 0102 | 0102 |
Перевод чисел из двоичной системы счисления в восьмеричную. Двоичное число делится на триады влево и вправо от запятой, отделяющей целую часть двоичного числа от дробной. Неполная старшая триада дополняется незначащими нулями слева, неполная младшая – незначащими нулями справа, значение числа при этом не изменяется. Затем каждая двоичная триада заменяется соответствующей ей восьмеричной цифрой. Например:
| 001| | 010| | 101|, | 0112 | = 125,38 | Добавленные в неполную старшую тетраду нули перечёркнуты. |
| ¯ | ¯ | ¯ | ¯ | ||
| 18 | 28 | 58 | 38 |
Перевод из шестнадцатеричной системы счисления в двоичную. Поскольку 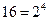 , то каждая шестнадцатеричная цифра эквивалентна группе из четырёх двоичных цифр (тетраде):
, то каждая шестнадцатеричная цифра эквивалентна группе из четырёх двоичных цифр (тетраде):
| Шестнадцатеричная цифра | А | В | С | D | E | F | ||||||||||
| Двоичная тетрада |
Для перевода из шестнадцатеричнойсистемы счисления в двоичную каждая цифра исходного шестнадцатеричногочисла заменяется соответствующей ей двоичной тетрадой:
| А | 2, | С8 | =1110100010,112 | При записи результирующего двоичного числа незначащие нули можно отбросить. | |
| ¯ | ¯ | ¯ | ¯ | ||
| 00112 | 10102 | 00102 | 11002 |
Перевод чисел из двоичной системы счисления в шестнадцатеричную. Двоичное число делится на тетрады влево и вправо от запятой, отделяющей целую часть двоичного числа от дробной. Неполная старшая тетрада дополняется незначащими нулями слева, неполная младшая – справа. Затем каждая двоичная тетрада заменяется соответствующей ей шестнадцатеричной цифрой. Например:
| 0101| | 1100| | 1001|, | 11102 | = 5С9,Е16 | Добавленные в неполные тетрады нули перечёркнуты. |
| ¯ | ¯ | ¯ | ¯ | ||
| 516 | С16 | 916 | Е16 |
Перевод из восьмеричной системы счисления в шестнадцатеричную выполняется через двоичную систему счисления: сначала восьмеричное число переводится в двоичную систему счисления; затем полученное двоичное число переводится в шестнадцатеричную систему счисления. Правила переводов изложены выше. Например:
| 3, | 58 | = 1111011,1012 = | 0111| | 1011|, | = 7В,А16 | |||
| ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ||
| 0012 | 1112 | 0112 | 1012 | 716 | В16 | А16 |
Перевод из шестнадцатеричной системы счисления в восьмеричную выполняется также через двоичную систему счисления: сначала шестнадцатеричное число переводится в двоичную систему счисления; затем полученное двоичное число переводится в восьмеричную систему счисления. Правила переводов изложены выше. Например:
| F | 0, | 316 | = 111110000,00112 = | 111| | 110| | 000|, | 001| | = 760,148 | ||
| ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ¯ | ||
| 00012 | 11112 | 00002 | 00112 | 78 | 68 | 08 | 18 | 48 |
Задача 1. Выполнить указанные в таблице задания
Варианты
| Вариант | Задания |
| 1. | Какие целые числа следуют за числами:

|
| 2. | Какие целые числа предшествуют числам:
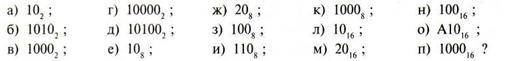
|
| 3. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а) 1101,12 и 101,12; б) А,В16 и E,F16. |
| 4. | Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а) 10110112; б) 10108. |
| 5. | Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а) 12510; б) 229,510 |
| 6. | Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а) 1001111110111,01112; г) 1011110011100,112; б) 1110101011,10111012; д) 10111,11111011112; в) 10111001,1011001112; е) 1100010101,110012. |
| 7. | Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: а) 2СЕ16; б) 9F40l6; в) CDE16 |
| 8. | Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а)51716; б) ABC16 |
| 9. | Выпишите целые числа: а) от 1011012 до 1100002; б) от 2023 до 10003; в) от 148 до 208; г) от 2816 до 3016. |
| 10. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а) 10111012 и 11101112; в) 378 и 758; д) А16 и F16. |
| 11. | Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем выполните обратные переводы: а) 8810; б) 37,2510 |
| 12. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: 1116, Е16, 916 и А16. |
| 13. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а) 1011,1012 и 101,0112; б 1658 и 378; в) 1916 и С16; |
| 14. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а) 10112,12 и 111,12; б) 7,58 и 14,68. |
| 15. | Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а) 10112, 11,12 и 1112; б) 68, 178 и78. |
| 16. | Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а) 101016; б) 12348 |
| 17. | Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а) 1F16; б) 5178 |
| 18. | Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: а) 1010,10116; б) 1ABC,9D16. |
| 19. | Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем выполните обратные переводы: а) 36; б) 206,12510. |
| 20. | В какой системе счисления выполнены следующие сложения? Найдите основания каждой системы:

|
Пример выполнения
Задача 1. Какое наибольшее десятичное число можно записать тремя цифрами в системах счисления: а) двоичной; б) восьмеричной; в) шестнадцатеричной?
Решение.
а) Так как в двоичной системе счисления старшая цифра равна 1, то наибольшее число, которое можно записать тремя цифрами равно 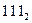 . В десятичной системе счисления:
. В десятичной системе счисления: 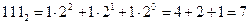 .
.
Второй способ. Несложно сообразить, что эта задача может быть решена и так:  . В десятичной системе счисления:
. В десятичной системе счисления:  ;
; 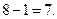
б) В восьмеричной системе счисления старшая цифра равна 7, поэтому наибольшее число, которое можно записать тремя цифрами равно 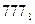 . Переведём его в десятичную систему счисления:
. Переведём его в десятичную систему счисления:  .
.
Второй способ: 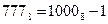 ;
; 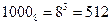 ;
; 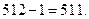
в) В шестнадцатеричной системе счисления старшая цифра равна F, поэтому наибольшее число, которое можно записать тремя цифрами равно 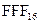 . Переведём его в десятичную систему счисления:
. Переведём его в десятичную систему счисления: 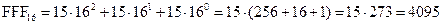 .
.
Второй способ. 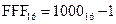 ;
;  ;
; 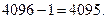
Ответ: а) 7; б) 511; в) 4095.
Задача 2. В какой системе счисления справедливо заданное равенство?
Варианты
| Вариант | Равенство | Вариант | Равенство |
| 1. | 20 + 25 = 100 | 11. | 22 + 55 = 110 |
| 2. | 25 + 35 = 104 | 12. | 88 + 24 = 101 |
| 3. | 23 + 32 = 121 | 13. | 22 + 45 = 111 |
| 4. | 111 – 33 = 45 | 14. | 88 + 44 = 110 |
| 5. | 99 + 67 = 100 | 15. | 89 + 78 = 101 |
| 6. | 50 + 50 = 120 | 16. | 14 + 34 = 103 |
| 7. | 35 + 25 = 104 | 17. | 31 + 46 = 110 |
| 8. | 24 + 68 = 103 | 18. | 11 + 55 = 110 |
| 9. | 23 + 32 = 110 | 19. | 17 + 77 = 105 |
| 10. | 71 + 21 = 112 | 20. | 55 + 34 = 111 |
Пример выполнения
Задача 2. В какой системе счисления справедливо равенство 22 + 44 = 110?
Решение. Пусть х – искомое основание системы счисления. Тогда  ;
; 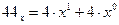 ;
; 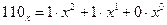 . Таким образом,
. Таким образом, 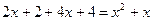 или
или 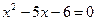 . Положительным корнем этого квадратного уравнения является
. Положительным корнем этого квадратного уравнения является  .
.
Ответ:  .
.
Задача 3. Найти основание x системы счисления, для которой выполняется равенство
Варианты
| Вариант | Равенство | Вариант | Равенство |
| 1. | 5510 = 210 х | 11. | 7910 = 211 х |
| 2. | 6210 = 142 х | 12. | 10610 = 211 х |
| 3. | 18810 = 161 х | 13. | 13310 = 111 х |
| 4. | 8110 = 311 х | 14. | 8410 = 150 х |
| 5. | 7010 = 130 х | 15. | 9910 = 120 х |
| 6. | 9010 = 110 х | 16. | 7010 = 240 х |
| 7. | 8410 = 220 х | 17. | 10110 = 245 х |
| 8. | 10910 = 131 х | 18. | 22010 = 190 х |
| 9. | 8710 = 322 х | 19. | 16110 = 188 х |
| 10. | 15110 = 128 х | 20. | 9210 = 161 х |
Пример выполнения
Задача 3. Найти основание x системы счисления, для которой выполняется равенство 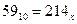 .
.
Решение. В десятичной системе счисления:  . Таким образом,
. Таким образом,  или
или 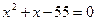 . Положительным корнем этого квадратного уравнения является
. Положительным корнем этого квадратного уравнения является  .
.
Ответ:  .
.
Задача 4. Вычислить значение заданного выражения в десятичной системе счисления. Перевести каждое число в двоичную систему счисления (с точностью до 4 разрядов после запятой). Выполнить все действия в двоичной системе счисления. Результат перевести в десятичную систему счисления. Определить погрешность вычисления как разность между результатами первого и последнего действий
Варианты
| Вариант | Выражение | Вариант | Выражение |
| 1. | 12,1 ´ 3 – 17,6 | 11. | 17,1 ´ 3 – 14,6 |
| 2. | 19,8: 2 – 7,4 | 12. | 11,7 ´ 3 – 12,4 |
| 3. | 11,3 ´ 3 + 6,6 | 13. | 27,5: 2 – 11,9 |
| 4. | 13,6 ´ 3 – 9,7 | 14. | 19,6 ´ 3 – 12,7 |
| 5. | 10,6 ´ 3 – 9,8 | 15. | 11,7 ´ 3 – 8,4 |
| 6. | 12,4 ´ 3 – 21,6 | 16. | 12,6 ´ 3 – 22,3 |
| 7. | 28,6: 2 – 10,8 | 17. | 10,3 ´ 3 – 19,7 |
| 8. | 17,3 ´ 3 + 4,9 | 18. | 23,5: 2 – 9,9 |
| 9. | 13,3 ´ 3 – 8,3 | 19. | 9,6 ´ 3 + 2,7 |
| 10. | 11,7 ´ 3 – 9,4 | 20. | 7,8 ´ 3 – 11,6 |
Пример выполнения
Задача 4. Вычислить значение выражения 7,9 ´ 3 – 12,6 в десятичной системе счисления. Перевести каждое число в двоичную систему счисления (с точностью до 4 разрядов после запятой). Выполнить все действия в двоичной системе счисления. Результат перевести в десятичную систему счисления. Определить погрешность вычисления как разность между результатами первого и последнего действий.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 652; Нарушение авторских прав?; Мы поможем в написании вашей работы!