Решение. 1) Вычисляем значение выражения в десятичной системе счисления:

1) Вычисляем значение выражения в десятичной системе счисления:

7,9 ´ 3 – 12,6 = 11,1

2) Переводим первое число 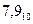в двоичную систему счисления.

Число 7,9 содержит целую часть (7) и дробную часть (0,9).

Для перевода целой части используем метод перевода целых чисел из десятичной системы счисления в двоичную. Согласно ему целое число делится на два нацело с записью целого частного и остатка от деления. Каждое полученное целое частное вновь делится на два до тех пор, пока частное от деления не станет равным нулю. Остатки от деления, записанные в порядке, обратном их получению, представляют искомое двоичное число.

Для перевода дробной части используем метод перевода дробных чисел из десятичной системы счисления в двоичную. Согласно ему цифры дробной части умножаются на два с раздельной записью целой и дробной частей произведения. Дробные части произведений вновь умножаются на два по тому же правилу до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо пока не будет вычислено заданное количество дробных двоичных цифр. Целые части произведений, записанные в порядке их получения, представляют цифры искомой двоичной дроби.

Выполним рассмотренные действия для нашего числа 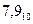. Дробную часть, согласно заданию, будем переводить до получения четырёх двоичных цифр за запятой.

Перевод целой части		Перевод дробной части
Частные	Остатки		Целые части	Дробные части
от деления на 2	от умножения дробных частей на 2
			0,
	1 ­		¯ 1
	1 ­		¯ 1
	1 ­		¯ 1
Получаем:	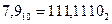	¯ 0

3) Переводим второе число 3₁₀ в двоичную систему счисления.

Частные	Остатки
от деления на 2
	1 ­
	1 ­	Получаем: 310 = 112

4) Переводим третье число 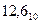в двоичную систему счисления.

Перевод целой части		Перевод дробной части
Частные	Остатки		Целые части	Дробные части
от деления на 2		от умножения дробных частей на 2
			0,
	0 ­		¯ 1
	0 ­		¯ 0
	1 ­		¯ 0
	1 ­		¯ 1

Таким образом, .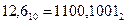

5) Выполняем умножение в двоичной системе счисления:	6) Выполняем вычитание в двоичной системе счисления:
	´	111,1110			.2.2
			-	10111,1010
			1100,1001
				1011,0001
	10111,1010

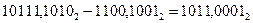
7) Переводим двоичный результат в десятичную систему счисления:

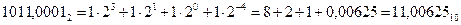
8) Вычисляем погрешность вычисления: 11,1 – 11, 00625 = 0,09375.

Ответ: Погрешность вычисления 0,09375.

Задача 5. Для заданного десятичного числа выполнить следующие преобразования систем счисления: 10’8’10’16’10; 8’16

Варианты

Вариант	Число	Вариант	Число	Вариант	Число	Вариант	Число
1.	1537810	6.	1147810	11.	1812410	16.	1319010
2.	1317810	7.	1479010	12.	1682310	17.	1290510
3.	1182310	8.	1539110	13.	1932110	18.	1702410
4.	1738910	9.	1499110	14.	1487610	19.	1821010
5.	1259210	10.	1329710	15.	1512810	20.	1476510

Пример выполнения

Задача 5. Для десятичного числа 15378₁₀ выполнить следующие преобразования систем счисления: 10’8’10’16’10; 8’16.

Дата добавления: 2014-12-16