Решение. 1) Переводим число в восьмеричную систему счисления

1) Переводим число 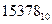в восьмеричную систему счисления. Для перевода используем метод деления этого числа на 8 нацело с записью частных и остатков от деления.

Частные	Остатки
от деления на 8	– 8
			-16
	2 ­		– 72		-24
	2 ­			-32		-24
	0 ­		– 16
	6 ­
	3 ­		– 16
Получаем: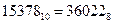

2) Переводим число 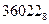в десятичную систему счисления:

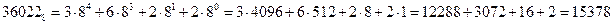
Получаем: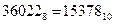

3) Переводим число 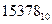в шестнадцатеричную систему счисления. Для перевода используем метод деления этого числа на 16 нацело с записью частных и остатков от деления.

Частные	Остатки
от деления на 16	–144
			–96
	2 ­		– 96		–48
	1 ­				12 = С
	С ­		– 16
	3 ­

Получаем: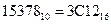

4) Переводим число 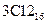в десятичную систему счисления:

.

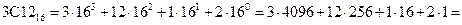
Получаем: .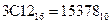

5) Переводим число 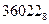в шестнадцатеричную систему счисления:

Сначала переводим 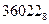в двоичную систему счисления. Далее разобьём полученное двоичное число на тетрады, начиная от нулевого разряда влево. Неполную старшую тетраду дополним незначащим нулём слева. Затем каждую тетраду заменим соответствующей ей шестнадцатеричной цифрой:

				28	=111100000100102 =	0011|	1100|	0001|	00102	= 3С1216
¯	¯	¯	¯	¯		¯	¯	¯	¯
0112	1102	0002	0102	0102		316	С16	116	216

Получаем: .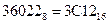

Ответ: ; ; ; ;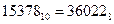
.

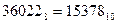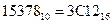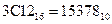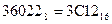ТЕМА 2. Представление информации

Методические указания

Ячейки памяти и машинные двоичные коды

Числа в памяти ЭВМ (компьютера) могут храниться в разных форматах. Термин «формат хранения» синонимичен понятию «внутримашинное представление» и является важнейшей составной частью понятия типа данных. В языках программирования типы данных имею собственные названия. Например, в языках Паскаль и Delphi (с версии среды Delphi 7.0 в официальных документах фирмы Borland в качестве названия языка программирования вместо Object Pascal стал использовать термин «Delphi») имеются типы числовых данных с названиями: Byte, Shortint, Word, Integer, Longint, Real, Single, Double, Extended, Comp.

Каждому типу числовых данных соответствует конкретная длина ячейки памяти ЭВМ, обозначим эту длину буквой 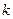. Ячейкой памяти принято называть участок основной памяти компьютера, выделяемый для хранения данных. Физически каждый элемент ячейки памяти – это устройство, называемое триггером. Триггер имеет два устойчивых состояния. Одно из этих состояний логически связывается со значением ноль, а другое – со значением единица. Таким образом, с логической точки зрения ячейка памяти – это последовательность разрядов, в которых размещаются двоичные цифры. Эти цифры часто называют битами.

Содержимое ячейки памяти – последовательность бит – называется машинным двоичным кодом. Естественно, любой двоичный код может быть рассмотрен (интерпретирован) как двоичное представление некоторого целого числа. Значение этого числа может быть равным нулю, – если все биты кода равны нулю, или положительным, – поскольку в двоичном коде нет иных знаков кроме двоичных цифр. Указанную числовую интерпретацию двоичного кода назовем арифметическим значением этого кода и обозначим его буквой U.

Может возникнуть вопрос: а что – возможны какие-то ещё интерпретации двоичных кодов? Чуть подумав, понимаем: конечно же, возможны. Дело в том, что двоичные коды не только интерпретируются (воспринимаются, толкуются) но и формируются. Процесс интерпретации двоичного кода – это, по сути дела, процесс чтения информации, а процесс формирования кода – это процесс записи информации в память компьютера. Ну, а записывать надо не только целые числа без знака, но и числа со знаком, и дробные числа, да и не только числа. Естественно, весь этот зоопарк разнотипных данных приходится отображать в последовательности единиц и нулей – иного в памяти ЭВМ нет! Таким образом, осознаём: двоичный код может означать всё, что угодно, а не только целое число без знака. И теперь понятна вся условность введённого нами понятия арифметического значения двоичного кода – это простейшая, выбранная нами именно по причине крайней простоты, интерпретация кода, который на самом деле может быть сформирован при занесении в память компьютера чего-то совершенно иного.

А как же всё-таки машина узнаёт о том, как ей надлежит интерпретировать содержимое ячеек собственной памяти? Дело в том, что понятие типа данных включает не только сведение о длине ячейки памяти, выделяемой под данные конкретного типа, но и еще два сведения: 1) правило формирования двоичного кода (правило кодирования) значения, помещаемого в ячейку; 2) правило интерпретации содержимого ячейки памяти, т. е. правило распознавания хранимого значения. Да-да, это правила записи и чтения информации! Встряхнём головой, вздохнём, и постараемся постичь следующее: для каждой ячейки памяти компьютера, используемой для хранения данных (чисел и прочее), выделяется ещё одна дополнительная – теговая ячейка памяти, предназначенная для хранения сведения о типе данных, хранимых в основной ячейке.

Итак, память ЭВМ «нарезается» на ассоциированные пары ячеек – ячейки хранения данных и теговые ячейки с информацией (кодом) о типе хранимых данных. Именно по коду в теговой ячейке машина выбирает нужное правило формирования двоичного кода значения, помещаемого в память, и правило выяснения значения, извлекаемого из памяти.

Итак, запоминаем:

· двоичный машинный код – это целое двоичное число без знака, записанное фиксированным количеством разрядов, возможно, с незначащими лидирующими нулями;

· это число называется кодом потому, что в него отображается путём кодирования нечто иное, например, целое число со знаком или дробное число;

· получается, что у кода имеется два значения: 1) числовое, поскольку код – это целое число (мы назвали это значение арифметическим), и 2) фактическое – исходное, из которого получается код путём каких-то вычислений.

Представление целых чисел без знака

Это всё очень просто: целое число без знака просто переводится в двоичную СС и слева дополняется незначащими нулями так, чтобы общее количество двоичных цифр равнялось 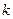– длине ячейки памяти, выделяемой под величины заданного типа.

Представление целых чисел со знаком

В современных компьютерах целые числа хранятся в дополнительном коде. Помимо дополнительного кода в теории известны, а в недалёком прошлом применялись и в реальных ЭВМ, прямой и обратный (инверсный) коды.

Чтобы осознать, – чем отличается машинный двоичный код числа от записи этого числа в двоичной системе счисления, следует знать следующие факты.

1. Запись числа в двоичной системе счисления, как и в десятичной, содержит только информационно необходимые цифры, незначащие нули практически никогда не записываются (за исключением специальных рассмотрений).

Машинный же код – это запись числа с помощью фиксированного количества разрядов – количества разрядов в выделяемой под число ячейки памяти ЭВМ. Например, однобайтные ячейки памяти содержат восьмибитные коды, при этом двоичное число 101 представляется в виде 00000101; это представление и называется однобайтным машинным кодом двоичного числа 101. Итак, машинный код положительного двоичного числа часто содержит незначащие лидирующие нули – это совсем просто!

2. В двоичной системе счисления, как и в десятичной, положительные числа могут записываться и без знака, например, 101, и со знаком, например, +101. Отрицательные числа всегда записываются только со знаком, например, –101.

Машинные двоичные коды знаков не имеют, они состоят только из двоичных цифр, называемых битами.

3. Общее количество кодов, представимых в k-битной ячейке памяти равно 2^k. Действительно, первый бит порождает две комбинации (0 и 1), каждая из этих комбинаций может быть взята с каждой из двух таких же комбинаций второго бита – получаем 4 комбинации, каждая из этих четырёх комбинаций может быть взята с двумя комбинациями третьего бита – получаем 8=2³ комбинации, и так далее до k-го бита.

4. Первая половина кодов (их количество, естественно, равно 2^k/2=2^k-1) выделяется для хранения неотрицательных чисел – нуля и положительных значений. Вторая половина кодов (их тоже 2^k-1) выделяется для хранения отрицательных чисел.

Замечательное следствие такого разделения кодов состоит в том, что коды всех неотрицательных чисел содержат в старшем (самом левом) бите ноль, а коды всех отрицательных чисел содержат в старшем бите единицу. Это следствие послужило основанием того, что во многих учебниках по информатике утверждается следующее: «… Старший разряд двоичного кода числа является знаковым: ноль кодирует знак плюс, а единица – знак минус». И скажите, что это не так!

5. Естественно, любая последовательность бит может быть интерпретирована как беззнаковое число – положительное или ноль. Мы называем эту интерпретацию арифметическим значением двоичного машинного кода и обозначаем буквой U.

Интерпретационная формула машинного кода целого числа имеет вид:

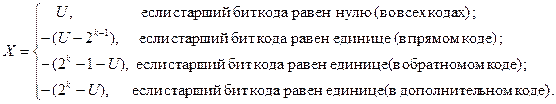(2)

Как видно из формулы (2), во всех кодах – и прямом, и обратном, и дополнительном хранимые положительные числа представляются таким образом, что арифметическое значение U двоичного машинного кода совпадает с хранимым значением Х.

Несложно догадаться, как получается двоичный машинный код неотрицательного числа – двоичное представление числа дополняется слева незначащими лидирующими нулями до k разрядов – длины ячейки памяти ЭВМ. С кодами отрицательных чисел несколько сложнее. В общем случае формулу генерации кода можно получить из формулы (2):

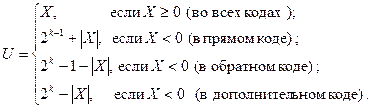(3)

Если последние две строчки у вас не получаются, то заметим, что при 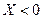имеем: 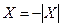и 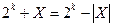. Естественно, предполагается, что результаты вычислений записываются в виде последовательности k бит.

Прямой код – самый простой. В нём используется представление числа в привычной форме: «знак»«абсолютная величина». При этом старший разряд ячейки отводится под знак, а остальные – под двоичный код абсолютной величины. Например, прямые коды двоичных чисел 1001 и –1001 для 8-разрядной ячейки таковы: 00001001 и 10001001 соответственно.

Обратный код положительного числа совпадает с его прямым кодом. Обратный код отрицательного числа Х представляет собой двоичный код числа U = 2^k – 1 – |Х|, где k – количество разрядов используемой ячейки памяти (в однобайтном формате k = 8). Код разности 2^k – 1 представляет собой k единиц, поэтому разность 2^k – 1 – |Х| получается очень просто: путём инвертирования разрядов прямого кода |Х| (единицы заменяются нулями, а нули – единицами). Таким образом, обратный код отрицательного числа образуется инвертированием разрядов прямого кода абсолютной величины этого числа. Например, обратный код двоичного числа –1001 для 8-разрядной ячейки таков: .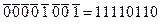

Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа Х представляет собой двоичный код числа U = 2^k – |Х|, где k, по-прежнему, – количество разрядов используемой ячейки памяти. Нетрудно понять, что дополнительный код отрицательного числа может быть получен путём прибавления единицы к обратному коду этого числа. Например, дополнительный код двоичного числа –1001 для 8-разрядной ячейки таков: .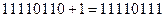

Представление вещественных чисел в типе Single

Согласно IEEE 754 двоичный код 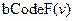числа 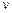типов Single и Double состоит из трёх полей: 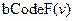= 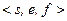, где s – знаковый бит (sign bit) числа; e – характеристика (exponent), на жаргоне программистов – экспонента; f – дробная часть мантиссы (fraction). Все компоненты кода принято рассматривать как целые неотрицательные числа.

Код 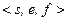имеет два первичных параметра: 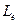– количество бит, выделяемых под характеристику 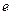; 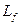– количество бит, выделяемых под дробную часть мантиссы 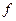, и несколько вторичных (вычисляемых) параметров, важнейшие из которых: 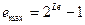– максимальное возможное значение характеристики (двоичный код 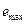состоит из 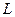единиц); 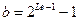– значение смещения порядка (двоичный код 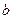состоит из 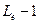единиц, обозначение происходит от английского bias – смещение); 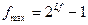– максимальное возможное значение дробной части мантиссы (двоичный код 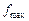состоит из 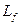единиц).

Интерпретация хранимого кода 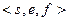осуществляется по формуле [1, 2]:

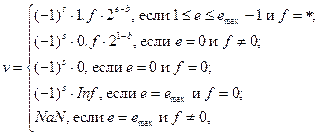(4)

где «*» – символизирует «любое возможное значение»; «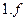» – мантисса нормализованного кода числа; «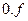» – мантисса денормализованного кода числа; 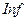– идентификатор неопределённости «бесконечность» (от английского Infinity); 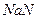– идентификатор неопределённости «не число» (от английского Not a Number), ему, в частности, соответствует результат деления 0/0.

Задача 6.Два числа X1 и X2 хранятся в формате 1 байт со знаком. Заданы их шестнадцатеричные коды. Чему равны их фактические десятичные значения?

Варианты

Вариант	X1	X2	Вариант	X1	X2
1.	CE16	5F16	11.	5B16	D416
2.	E916	5C16	12.	9A16	В816
3.	E716	8D16	13.	C316	9B16
4.	1516	BC16	14.	3E16	F416
5.	A116	3E16	15.	FF16	1216
6.	1F16	AB16	16.	3E16	C716
7.	FD16	4A16	17.	E416	5F16
8.	D516	7916	18.	5B16	AА16
9.	B816	6E16	19.	B616	7C16
10.	D016	8C16	20.	A916	8D16

Пример выполнения

Задача 6. Два числа хранятся в формате 1 байт со знаком. Заданы их шестнадцатеричные коды: X1 = 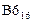, X2 = 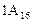. Чему равны их фактические десятичные значения?

Дата добавления: 2014-12-16