
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Тип Single предназначен для хранения вещественных (действительных) чисел в формате с длинами полей кода =
|
|
|
|
Тип Single предназначен для хранения вещественных (действительных) чисел в формате 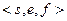 с длинами полей кода
с длинами полей кода  =
= 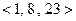 .
.
Представим заданный код 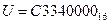 в двоичной СС. Для этого запишем двоичный код каждой шестнадцатеричной цифры в виде тетрады (четвёрки) бит:
в двоичной СС. Для этого запишем двоичный код каждой шестнадцатеричной цифры в виде тетрады (четвёрки) бит:
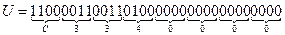
На основе записанного кода и длин полей кода определяем составные части кода числа 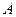 :
:
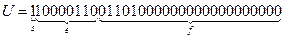 ;
;
 ;
; 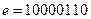 ;
; 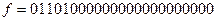
Значение 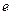 удовлетворяет условию
удовлетворяет условию 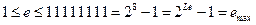 , следовательно, необходимо использовать первую строку интерпретационной формулы (4) для кодов Single и Double:
, следовательно, необходимо использовать первую строку интерпретационной формулы (4) для кодов Single и Double: 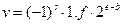 .
.
В нашем случае имеем:
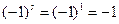 ;
;
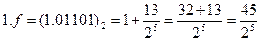 ;
;
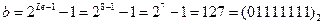 ;
;
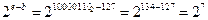 ;
;
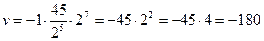 .
.
Ответ: 32 разряда памяти компьютера
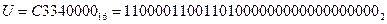
в формате типа Single соответствует десятичному значению –180.
Замечание: в процессе вычисления конструкции 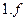 использовалась следующая формула перевода дроби из двоичного представления в десятичное:
использовалась следующая формула перевода дроби из двоичного представления в десятичное:
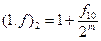 ,
,
где 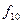 – десятичное представление значения
– десятичное представление значения 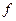 ;
; 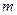 – количество двоичных цифр в записи
– количество двоичных цифр в записи 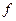 .
.
ТЕМА 3. Основы алгебры логики
Методические указания
Таблицы истинности основных логических операций
| Отрицание | Дизъюнкция (логическое сложение) | Конъюнкция (логическое умножение) | Исключающее ИЛИ (сложение по модулю 2) | ||||||||||
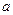
| 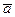
| 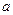
| 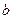
| 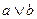
| 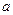
| 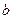
| 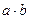
| 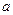
| 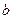
| 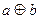
| |||
Приоритеты выполнения логических операций в порядке убывания
| Приоритет | Операция | |
| ¯ | Отрицание | |
| ¯ | Логическое умножение | |
| ¯ | Логическое сложение, исключающее ИЛИ | |
| Операции в скобках выполняются в первую очередь |
Законы и тождества алгебры логики
| № | Название | Для операции ИЛИ | Для операции И | |||
| Основные законы | ||||||
| 1. | Коммутативность, переместительность | 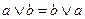
| 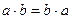
| |||
| 2. | Ассоциативность, сочетательность | 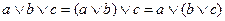
| 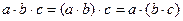
| |||
| 3. | Дистрибутивность, распределительность | дизъюнкции относительно конъюнкции
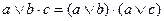
| конъюнкции относительно дизъюнкции 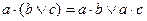
| |||
| 4. | Де Моргана | 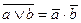
| 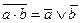
| |||
| Действия с одной переменной и константами | ||||||
| 5. | Свойства констант | 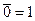
| 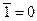
| |||
| 6. | Операция с 0 | 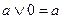
| 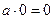
| |||
| 7. | Операция с 1 | 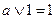
| 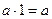
| |||
| 8. | Идемпотентность | 
| 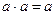
| |||
| 9. | Комплементность, дополнительность | 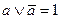
| 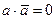
| |||
| 10. | Отрицание отрицания | 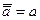
| ||||
| Дополнительные правила | ||||||
| 11. | Поглощения | 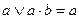
| 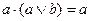
| |||
| 12. | Блейка-Порецкого | 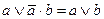
| 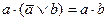
| |||
| 13. | Склеивания | 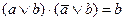
| 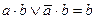
| |||
Задача 9.Вычислить значение логического выражения на заданном наборе логических переменных.
Варианты
| Вариант | Логическое выражение, набор переменных | Вариант | Логическое выражение, набор переменных |
| 1. | 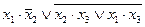 , (011). , (011).
| 11. | 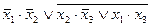 , (110) , (110)
|
| 2. |  , (001) , (001)
| 12. | 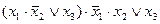 , (101) , (101)
|
| 3. | 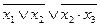 , (101). , (101).
| 13. | 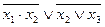 , (100) , (100)
|
| 4. | 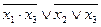 , (000) , (000)
| 14. | 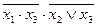 , (010) , (010)
|
| 5. | 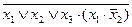 , (011). , (011).
| 15. | 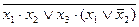 , (100). , (100).
|
| 6. | 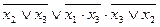 , (110). , (110).
| 16. | 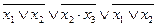 , (111) , (111)
|
| 7. | 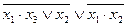 , (101). , (101).
| 17. |  , (100) , (100)
|
| 8. | 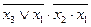 , (011) , (011)
| 18. | 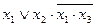 , (110) , (110)
|
| 9. | 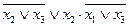 , (110). , (110).
| 19. | 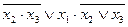 , (011) , (011)
|
| 10. | 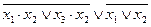 , (011). , (011).
| 20. | 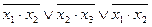 , (010) , (010)
|
Пример выполнения
Задача 9. Вычислить значение логического выражения 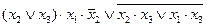 на наборе переменных (011).
на наборе переменных (011).
Решение. Задан набор переменных (011), это значит: 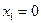 ,
, 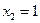 ;
; 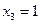 . Выполним операции в заданном выражении в соответствии с их порядком следования и приоритетами. Для этого разобьём выражение на два слагаемых.
. Выполним операции в заданном выражении в соответствии с их порядком следования и приоритетами. Для этого разобьём выражение на два слагаемых.
Первое слагаемое выражения:
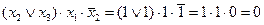 .
.
Второе слагаемое выражения:
 .
.
Сумма слагаемых:
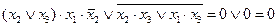 .
.
Ответ: значение выражения на наборе (011) равно 0.
Задача 10.Проверить справедливость равенства, используя законы алгебры логики.
Варианты
| Вариант | Равенство | Вариант | Равенство |
| 1. | 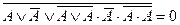
| 11. | 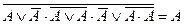
|
| 2. | 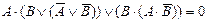
| 12. | 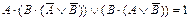
|
| 3. | 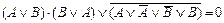
| 13. | 
|
| 4. | 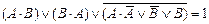
| 14. | 
|
| 5. | 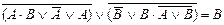
| 15. | 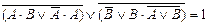
|
| 6. | 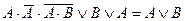
| 16. | 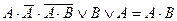
|
| 7. | 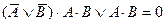
| 17. | 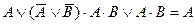
|
| 8. | 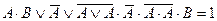
| 18. | 
|
| 9. | 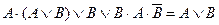
| 19. | 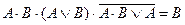
|
| 10. | 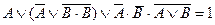
| 20. | 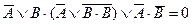
|
Пример выполнения
Задача 10. Проверить справедливость равенства 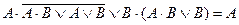 с использованием законов и тождеств алгебры логики.
с использованием законов и тождеств алгебры логики.
Решение. В соответствии с законами и тождествами алгебры логики упростим левую часть равенства. Сначала рассмотрим выражение с отрицанием:
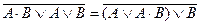 – по законам коммутативности и ассоциативности.
– по законам коммутативности и ассоциативности.
В этом выражении 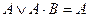 – по правилу поглощения.
– по правилу поглощения.
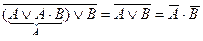 – по закону Де Моргана.
– по закону Де Моргана.
Первое слагаемое левой части равенства:
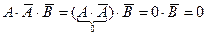 – коммутативность, дополнительность, операция с 0.
– коммутативность, дополнительность, операция с 0.
Второе слагаемое левой части равенства:
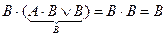 – использованы правила поглощения и идемпотентности.
– использованы правила поглощения и идемпотентности.
Всё выражение левой части равенства: 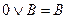 .
.
Ответ: 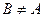 , равенство не справедливо.
, равенство не справедливо.
Задача 11.Упростить логическое выражение, используя законы алгебры логики
Варианты
| Вариант | Логическое выражение | Вариант | Логическое выражение |
| 1. | 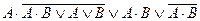
| 11. | 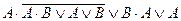
|
| 2. | 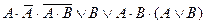
| 12. | 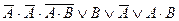
|
| 3. | 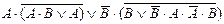
| 13. | 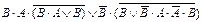
|
| 4. | 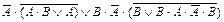
| 14. | 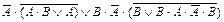
|
| 5. | 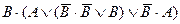
| 15. | 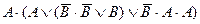
|
| 6. | 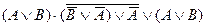
| 16. | 
|
| 7. | 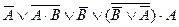
| 17. | 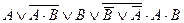
|
| 8. | 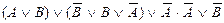
| 18. | 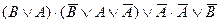
|
| 9. | 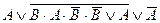
| 19. | 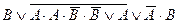
|
| 10. | 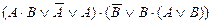
| 20. | 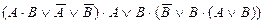
|
Пример выполнения
Задача 11. Упростить логическое выражение 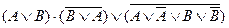 , используя законы и тождества алгебры логики.
, используя законы и тождества алгебры логики.
Решение. Рассмотрим первое слагаемое заданного выражения:
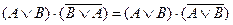 – по закону переместительности.
– по закону переместительности.
Обозначим 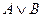 за
за 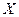 , тогда первое слагаемое примет вид
, тогда первое слагаемое примет вид
 – по правилу дополнительности.
– по правилу дополнительности.
Второе слагаемое:
 – дополнительность, логическое сложение, отрицание.
– дополнительность, логическое сложение, отрицание.
Всё выражение 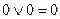 – по правилу выполнения логического сложения.
– по правилу выполнения логического сложения.
Ответ: 0.
Варианты заданий К КОНТРОЛЬНОЙ РАБОТЕ
| Номер в списке | Номера вариантов задач | ||||||||||||||||||||
| Задача 1 | Задача 2 | Задача 3 | Задача 4 | Задача 5 | Задача 6 | Задача 7 | Задача 8 | Задача 9 | Задача 10 | Задача 11 | |||||||||||
| группа 0 | |||||||||||||||||||||
| группа 1 | |||||||||||||||||||||
| группа 2 | |||||||||||||||||||||
| группа 3 | |||||||||||||||||||||
Литература
1.IEEE 754-1985 // Wikipedia – The free Encyclopedia [Электронный ресурс] – Электрон. дан. – URL: http://en.wikipedia.org/wiki/IEEE_754-1985
2.IEEE Standard for Binary Floating-Point Arithmetic. Copyright 1985 by The Institute of Electrical and Electronics Engineers, Inc. 345 East 47th Street, New York, NY 10017, USA. [Электронный ресурс] – Электрон. дан. – URL: http://kfe.fjfi.cvut.cz/~klimo/nm/ieee754.pdf
3.Можно пользоваться любыми учебниками по информатике. Многие из них можно найти в Интернет, набрав в браузере «Учебники по Информатике». Одновременно следует внимательнее изучать указания в данном пособии, тогда учебник может не понадобиться вовсе.
| ПРИЛОЖЕНИЕ А. кодировка символов Кодировка символов с десятичными кодами от 32 до 126 в соответствии со стандартами ASCII (DOS) и ANSI (Windows) | ||||||||||||
| Код | Символ | Код | Символ | Код | Символ | Код | Символ | Код | Символ | Код | Символ | |
| @ | P | ` | p | |||||||||
| ! | A | Q | a | q | ||||||||
| " | B | R | b | r | ||||||||
| # | C | S | c | s | ||||||||
| $ | D | T | d | t | ||||||||
| % | E | U | e | u | ||||||||
| & | F | V | f | v | ||||||||
| ' | G | W | g | w | ||||||||
| ( | H | X | h | x | ||||||||
| ) | I | Y | i | y | ||||||||
| * | : | J | Z | j | z | |||||||
| + | ; | K | [ | k | { | |||||||
| , | < | L | \ | l | | | |||||||
| - | = | M | ] | m | } | |||||||
| . | > | N | ^ | n | ~ | |||||||
| / | ? | O | _ | o | ||||||||
Русские буквы
ASCII:А…Я – 128…159; Ё – 240; а…п – 160…175; р…я – 224…239; ё – 241.
ANSI (шрифты Arial Cyr, Courier New Cyr, Times New Roman Cyr):
А…Я – 192…223; Ё – 168; а…я – 224…255; ё – 184.
ПРИЛОЖЕНИЕ Б.
Шаблон оформления титульного листа
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1400; Нарушение авторских прав?; Мы поможем в написании вашей работы!