Г.Т.Тухтиева 1 страница

В30.

В29.

В28.

В27.

В26.

В25.

В24.

В23

В22.

В21.

В20.

В19.

На соревнованиях по волейболу 16 команд разбиты случайным образом на две подгруппы по 8 команд в каждой. Определить вероятность того, что а) две наиболее сильные команды окажутся в разных подгруппах, б) две наиболее сильные команды окажутся в одной подгруппе.

В18.

В17.

В16.

В15.

В14.

В13.

В12.

В11.

В10.

В9.

В8.

В7.

В6.

В5.

В4.

В3.

В2.

В1.

ТР-9 (теория вероятностей)

Протокол № 1 от «27» августа 2014г.

Главная | Трудовой кодекс РФ | Статья 417. Ответственность работников за незаконные забастовки

Статья 417. Ответственность работников за незаконные забастовки

Работники, приступившие к проведению забастовки или не прекратившие ее на следующий рабочий день после доведения до органа, возглавляющего забастовку, вступившего в законную силу решения суда о признании забастовки незаконной либо об отсрочке или о приостановке забастовки, могут быть подвергнуты дисциплинарному взысканию за нарушение трудовой дисциплины.

(в ред. Федерального закона от 30.06.2006 N 90-ФЗ)

(см. текст в предыдущей редакции)

Представительный орган работников, объявивший и не прекративший забастовку после признания ее незаконной, обязан возместить убытки, причиненные работодателю незаконной забастовкой, за счет своих средств в размере, определенном судом.

Вопросы обсуждены и одобрены на заседании кафедры гражданско-правовых дисциплин

Заведующий кафедрой Л.В. Зарапина

1. Алгебраические операции над событиями.

2. Классическая схема (непосредственное вычисление вероятности).

3. Геометрическая вероятность.

4. Теоремы сложения и умножения.

5. Формула полной вероятности.

6. Схема Бернулли.

7. Дискретная случайная величина.

8. Непрерывная случайная величина.

9. Распределение Пуассона.

10.Нормальное распределение.

1. Мишень состоит из трех кругов, образованных концентрическими окружностями. Событие А_k (к=1,2,3) - попадание в круг радиуса r_k (r₁<r₂<r₃). Что означают события: А=А₁А₂А₃, B=A₁+A₂+A₃ , C=A₁A₂?

2. Номер состоит из 6 цифр. Определить вероятность того, что а) все числа номера различны; б) номер делится на пять.

3. Какова вероятность того, что сумма двух наудачу взятых отрезков, длина которых не превосходит Т, будет больше Т?

4. Из трех орудий произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9, из второго -0,8, из третьего - 0,6. Найти вероятность того, что только одно орудие попадет в цель.

5. В первой урне 2 белых и 5 черных шаров, во второй - 5 белых и 2 черных. Из первой урны во вторую переложили один шар, затем из второй урны извлекли один шар. Определить вероятность того, что взятый из второй урны шар - белый.

6. Вероятность сбоя в работе телефонной станции при каждом вызове = 0,1. Поступило 5 вызовов. Найти вероятность того, что сбоев точно три.

7. Дискретная случайная величина Х - число сбоев в предыдущей задаче. Найти 1) ряд распределения; 2 ) функцию распределения и ее график; 3) мат. ожидание; 4) дисперсию и СКВО; 5) вероятность попадания Х в промежуток 2; З.

8. Дана функция распределения непрерывной случайной величины:

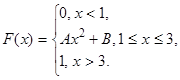
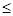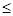Найти: А, В, мат. ожидание М[Х], дисперсию D[Х], плотность вероятностей, Р(0 Х 2).

9. Завод отправляет на базу 500 изделий. Известно, что р - вероятность повреждения изделия в пути, мала. Найти р, если вероятность того, что в пути будет повреждено хотя бы одно изделие, равна 0,98.

10. Случайная величина Х - измерение диаметра вала, подчинена нормальному закону с параметрами (0;20). Найти вероятность того, что из 3-х независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.

1. Из таблицы случайных чисел наудачу взято число. Рассмотрим два события: А - число делится на 5; В -число оканчивается нулем. Что означают события АВ; А+В; А 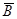; 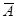В; ?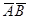

2. Урна содержит 6 белых и 4 черных шара. Одновременно извлекаются два шара, Определить вероятность того, что А) оба шара черные; Б) один черный, другой белый.

3. Значения а и b равновозможны в квадрате |а| , |b| . Найти вероятность того, что корни трехчлена x²+2ax+b - действительны.

4. Абонент забыл последнюю цифру номера телефона и потому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более чем, в три места.

5. Из 1000 ламп 200 принадлежит 1 - ой партии, 300 - 2 -ой, 500 - 3-ей. В первой партии 6%, во второй 5%, в третьей 4% бракованных ламп. Определить вероятность того, что наудачу выбранная лампа - бракованная.

6. Три монеты одновременно подбрасываются 3 раза. Определить вероятность того, что ровно в одном подбрасывании появится три: "герба".

7. Дискретная случайная величина Х - число появления трех "гербов" в предыдущей задаче. Найти: 1) ряд распределения, 2 ) построить функцию распределения, 3) М[Х], 4) D[Х], 5) CKBO, 6) P{X>1}.

8. Дана плотность распределения

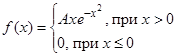
Найти A, F(x), М[Х], D[Х], P{X<М(Х)}.

9. Учебник издан тиражом 1000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,002. Найти вероятность того, что тираж содержит ровно три бракованных книги.

10. Производится взвешивание вещества. Случайная ошибка взвешивания подчинена нормальному закону с параметрами (0,20). Определить вероятность того, что при 3-х независимых взвешиваниях только в одном ошибка по абсолютной величине не превосходит 10 г.

1. Рабочий берет три детали из ящика. Событие А- хотя бы одна из 3-х деталей бракованная; В- не менее двух из 3-х бракованные. Что означают события ?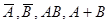

2. В группе из 25 студентов 8 учатся отлично, 7 хорошо, 5 удовлетворительно, 5 плохо. Преподаватель взял наугад 2-х студентов. Определить вероятность того, что а) оба учатся отлично; б) один отлично, другой плохо.

3. Наудачу взяты два положительных числа, каждое не превышает двух. Определить вероятность того, что и их сумма не превышает двух.

4. В первой урне 5 белых, 11 черных, 8 красных шаров, Во второй соответственно 10, 8, 6. Из обеих урн извлекают по одному шару. Какова вероятность, что оба шара одного цвета?

5. В альбоме 10 чистых и 5 гашеных марок. Из них наугад берут одну марку и подвергают спецгашению и возвращают в альбом. После этого берут одну марку. Определить вероятность того, что она чистая.

6. Вероятность поражения крейсера торпедой равна 0,4. Произведено четыре залпа. Определить вероятность того, что крейсер остался невредим.

7. Случайная величина Х - число попаданий в предыдущей задаче. Найти:1) ряд распределения, 2) построить функцию распределения, 3)М[Х], 4)D[Х], 5)СКВО, 6)Р{Х 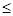2}.

8. Функция распределения непрерывной случайной величины задана формулой:

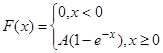
Найти A, f(x), M[X], D[Х], P{0<X<1}.

9. Среднее число вызовов, полученных телефонисткой в час равно 120. Какова вероятность, что в ближайшую минуту она не получит вызов?

10. Автомат изготовляет шарики. Шарик считается годным, если отклонение диаметра шарика от проектных размеров (Х) по абсолютной величине меньше 0,7 мм. х распределена нормально с параметрами (0; 0,4). Найти вероятность того, что среди 5 проверенных шариков все годные, если измерения производились независимо.

1. В урне черные и белые шары. Взяли два шара. Событие A- хотя бы один из двух шаров черный. B - оба шара черные. Что означают события ?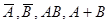

2. Ребенок играет с буквами разрезной азбуки А, А, А, К, Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово АТАКА?

3. На перекрестке установлен светофор, в котором 1 минуту горит зеленый свет и 0,5 мин. - красный. Затем все повторяется. В случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность, что он проедет перекресток без остановки?

4. Работают одновременно 3 радиолокационные станции, которые засекают некоторый объект с вероятностями 0,1; 0,2; 0,3. Определить вероятность того, что а) хотя бы одна из радиолокационных станций засечет объект; б) все станции засекут объект.

5. В магазин поступили однотипные изделия с 3-х заводов, причем 1-й завод поставляет 20% изделий, 2-ой - 30%, 3-й - 50%. Среди изделии 1-го завода 80%, 2-го - 60%, 3-го - 50% первосортных. Определить вероятность купить первосортное изделие.

6. Что вероятнее выиграть у равносильного противника (ничейный исход исключен) три партии из пяти или пять из восьми?

7. Случайная величина Х задана рядом распределения

X
P	0,1	0,6	a

Найти: 1) a, 2)M[X], 3) D[Х], 4 ) P{4 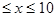}, 5) Функцию распределения и ее график.

8. Дана плотность распределения f(x)=Ae^–|x|.Найти: А, F(x), М[Х], D[Х], P{|x|<1}.

9. С накаленного катода вылетает в среднем 10 электронов в секунду. Какова вероятность, что за промежуток 2 секунды вылетит точно 20 электронов?

10. В нормально распределенной совокупности 15% значений Х меньше 12 и 40% больше 16,2. Найти среднее значение и стандартное отклонение данного распределения.

1. Из колоды карт вынимают две карты. Событие А - хотя бы одна карта черной масти; В - обе карты черной масти. Что означают события ?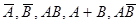

2. Числа 1,2,..,n расставлены случайным образом. Найти вероятность того, что числа 1 и 2 расположены рядом.

3. На отрезке ОА длины 21 см наудачу бросается точка В. Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую, чем 7 см.

4. В урне 2 белых, 3 черных, 5 красных шаров. Вынимают по очереди три шара. Определить вероятность того, что последние два шара красные.

5. Имеются две партии изделий по 12 и 10 штук, причём в каждой партии одно бракованное. Одно изделие из 1 партии переложили во вторую. Определить вероятность извлечения бракованного изделия из 2 партии.

6. вероятность отказа каждого прибора при испытании не зависит от отказов остальных и равна 0,2. Испытано 9 приборов. Найти вероятность того, что отказало не менее шести приборов.

7. Случайная величина Х- число отказавших приборов в предыдущей задаче. Найти: 1) ряд распределения, 2) функцию распределения и ее график, 3) М[Х], 4)D[Х], 5)СКВО, 6)P{x>3}.

8. Функция распределения непрерывной случайной величины задана формулой

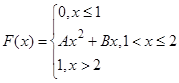
Найти: А, В, М[Х], D[Х], f(x), P{x>3}.

9. Проводятся испытания 1000 образцов на усталость. Вероятность поломки для каждого в течение суток 0,001. Найти вероятность того, что в течение суток сломается менее 2-х образцов.

10. Случайная величина Х- измерение диаметра вала подчинена нормальному закону с параметрами (0,20). Найти вероятность того, что в двух независимых измерениях ошибка по абсолютной величине не менее 4 мм.

1. События А - хотя бы один из 3-х проверяемых приборов бракованный, В - все приборы доброкачественные. Что означают события ?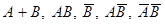

2. Имеется 15 изделий, из них 5 бракованных. Для контроля наудачу берутся 2 изделия. Определить вероятность того, что а) брак не обнаружен; б) одно изделие бракованное, другое нет.

3. На плоскость с нанесенной сеткой квадратов со стороной 3 см наудачу бросают монету радиуса 1 см. Найти вероятность того, что монета не пересчет ни одной из сторон квадрата.

4. При повышении напряжения в сети машина А выходит из строя с вероятностью 0,1, а машина В - с вероятностью 0,2. Определить вероятность того, что а)обе машины выйдут из строя; б)хотя бы одна из машин выйдет из строя, если машины выходят из строя независимо друг от друга.

5. В 1-ой урне 2 белых и 5 черных шаров, во 2-ой - 5 белых и 2 черных. Из 1-ой во 2-ую переложили один шар, затем из 2-ой урны извлекли один шар. Определить вероятность того, что шар, извлеченный из 2-ой урны - черный.

6. Вероятность сбоя в работе телефонной станции при каждом вызове 0,2. Определить вероятность того, что при 5 вызовах число сбоев не более двух.

7. Случайная величина Х- число сбоев в предыдущей задаче. Найти 1) ряд распределения, 2)функцию распределения и ее график, 3) М[Х], 4)D[Х], 5)СКВО, 6)P{x>4}.

8. Плотность распределения

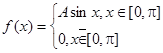
Найти А, М[Х], D[Х], P{x> 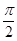}, F(x).

9. Сеанс дальней связи подводной лодки длится 21 сек. При этом наблюдаются атмосферные помехи в среднем 1000 в час. Найти вероятность отсутствия помех во время сеанса подводной лодки.

10. Диаметр втулки распределен нормально с параметрами (2; 0,01). В каких границах можно практически гарантировать диаметр втулки.

1. Пусть А₁,А₂,А₃ - произвольные события. Найти выражение для событий: А- произошло точно два события из трех, В- ни одно не произошло.

2. Среди 10 лотерейных билетов 3 выигрышные. Наудачу взяли 2 билета. Определить вероятность того, что а) оба билета выиграли, б) один выиграл, 2-ой нет.

3. В круге радиуса R проводят хорды 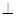диаметру. Определить вероятность того, что длина случайно взятой хорды не более R/3.

4. Вероятность хотя бы одного попадания в цель при 2-х независимых выстрелах равна 0,75. Найти вероятность двух попаданий при двух выстрелах.

5. В альбоме 10 чистых и 5 гашеных марок. Из них наудачу берут одну марку и подвергают спецгашению, затем возвращают в альбом. После этого берут одну марку. Найти вероятность того, что она гашеная.

6. Вероятность того, что при 5 вызовах сбой в работе телефонной станции произойдет хотя бы один раз, равна 0,375. Найти вероятность сбоя при одном вызове, если она одинакова при любом вызове и вызовы независимы.

7. Случайная величина Х задана рядом распределения

Х	-1
Р	0.2	0.3	0.4	а

Найти: 1)а, 2)функцию распределения и ее график, 3)М[Х], 4)D[Х], 5)СКВО, 6)P{x>3}.

8. Функция распределения непрерывной случайной величины задается формулой

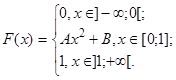
Найти А, В, М[Х], D[Х], f(x), P{-4 }

9. Имеем 2000 элементов. Вероятность отказа любого элемента за сутки 0,001. Найти среднее число отказавших за сутки элементов и вероятность того, что все элементы целы.

10. Ошибки измерений прибора подчиняются нормальному распределению. Прибор имеет систематическую ошибку 2 см и среднюю квадратичную ошибку 3 см. Найти вероятность того, что четыре ошибки измерений попадут в интервал ]0,4см[. Измерения независимы.

1. Прибор состоит из 2-х блоков 1-го и 3-х блоков 2-го типа. События А_к (к=1,2)-исправлен к -ый блок 1-го типа; Вj (j= 1,2,3) – исправленный j -ый блок 2-го типа. Прибор исправен, если исправен хотя бы один блок 1-го типа и не менее 2-х блоков 2-го типа. Выразить событие С -исправность прибора через А_к и B_j.

2. Найти вероятность того, что при шести бросаниях игральной кости появятся все грани.

3. На плоскости проведены параллельные линии, расстояние между которыми попеременно равны 2 и 10 см. Определить вероятность того, что наудачу брошенный на эту плоскость круг радиуса З см не будет пересечен ни одной линией.

4. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент не знает хотя бы один из 3-х предложенных ему вопросов.

5. Имеются две урны, в каждой 5 белых и 3 черных шара. Из каждой урны извлекают по одному шару, и затем из этих двух шаров наудачу берут один. Какова вероятность, что шар белый?

6. При передаче сообщения вероятность искажения одного знака 0,1. Передано сообщение из З‑х знаков. Определить вероятность того, что сообщение содержит не более двух искажений.

7. Случайная величина Х - число "искажений" в предыдущей задаче. Найти: 1) ряд распределения; 2) функцию распределения и ее график 3) MX, 4)D[Х], 5)CKBO, 6) P{‑1 }.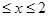

8. Функция распределения непрерывной случайной величины задана формулой

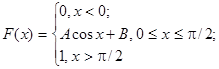
Найти: А, В, f(x), М[Х], D[Х], P{0 }.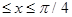

9. Устройство состоит из 100 000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента в течение суток 0,0001. Найти вероятность того, что за сутки откажут ровно три элемента.

10. Случайная величина х - измерение диаметра вала, подчинена нормальному закону с параметрами (0, 20),.Найти вероятность того, что в 3-х независимых измерениях ошибка 2-х измерений по абсолютной величине не менее 4 мм.

1. Судно имеет одно рулевое устройство, четыре котла и две турбины. Событие А- исправность рулевого устройства; В_к- исправность К-го котла (к=1,2,3,4); С_j- исправность j-ой турбины (j=1,2); Д - судно управляемо если исправно рулевое устройство, хотя бы один котел, хотя бы одна турбина. Выразить Д через А, В_к, С_j.

2. В лифт 5-этажного дома сели 3 пассажира. Каждый равновероятно может выйти на любом этаже. Определить вероятность того, что все вышли на разных этажах.

3. Даны две концентрические окружности радиусов r₂>r₁ c общим центром. На большей окружности наудачу ставятся две точки А и В. Какова вероятность того, что отрезок АВ не пересекает малую окружность?

4. Система состоит из двух приборов, дублирующих друг друга. При выходе из строя одного из приборов происходит мгновенное переключение на второй. Надежность (вероятность безотказной работы прибора) каждого прибора равны 0,7 и 0,8 соответственно. Определить надежность системы.

5. В первой урне 1 белый и 9 черных шаров, во 2-ой -1 черный и 5 белых. Из каждой урны берут по одному шару. Оставшиеся шары ссыпают в третью урну. Определить вероятность того, что шар, взятый из 3-ьей урны - белый.

6. Что вероятнее выиграть у равносильного противника (ничейный исход исключен) не менее 3-х партий из 4-х или не менее 6 партий из 8.

7. Случайная величина Х задана рядом распределения

Х	-1
Р	а	0,3	0,4	0,1

Найти 1)а, 2)функцию распределения и ее график, 3)М[Х], 4)D[Х], 5)СКВО, 6)P{x 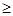1}

8. Дана плотность распределения

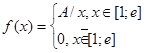
Найти А, F(x), М[Х], D[Х], P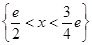

9. Станок-автомат штампует детали. Вероятность Р того, что деталь бракованная мала. Найти Р, если вероятность того, что среди 500 деталей все небракованные есть 0,02.

10. Автомат изготовляет шарики. Шарик - годный, если отклонение диаметра шарика Х от нормы по абсолютной величине меньше 0,7 мм. Х - распределена нормально с параметрами (0;0,4). Найти вероятность того, что из 5 проверенных шариков хотя бы один годный. Измерения независимы.

1. Экзаменационный билет содержит 3 вопроса. События: А-студент знает 1-ый вопрс; В- 2-ой вопрс; С- 3-ий; Д- студент сдал экзамен. Студент сдает экзамен, если знает хотя бы два вопроса. Выразить событие Д через А, В, С.

2. Какова вероятность того, что четырехзначный номер автомобиля а) имеет точно две цифры разные; б)четный.

3. Два студента договорились встретиться в институте в течение часа. Время ожидания одного другим 10 мин. Определить вероятность их встречи.

4. Вероятность прорыва эсминца на первой линии мин равна 0,3, на второй- 0,4. Определить вероятность того, что эсминец проскочит обе линии мин.

5. Из урны, содержащей 3 белых и 5 красных шаров, утеряно 2 шара. Найти вероятность извлечения белого шара.

6. Вероятность рождения мальчика и девочки одинаковы. Какова вероятность, что среди 6 наудачу отобранных новорожденных число мальчиков и девочек одинаково.

7. Случайная величина Х задана рядом распределения

Х	-3	-1
Р	0,15	а	0,3	0,05	0,10	0,20

Найти 1)а, 2)функцию распределения и ее график, 3)М[Х], 4)D[Х], 5) СКВО, 6)P{0 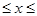2}

8. Функция распределения непрерывной случайной величины имеет вид

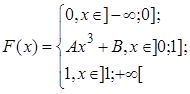
Найти А, В, f(x), М[Х], D[Х], P{0<x 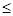2}

9. Завод отправил в магазин 1000 бутылок минеральной воды. Вероятность, что одна бутылка разобьется в пути равна 0,001. Найти вероятность того, что в пути разобьется хотя бы одна бутылка.

10. Случайная ошибка измерения подчинена нормальному закону с параметрами (0,20). Найти вероятность того, что при 2-х независимых измерениях ошибка хотя бы одного не превзойдет по абсолютной величине 4мм.

1. Прибор состоит из 2-х блоков 1-го и 3-х 2-го типа. События: А_к (К=1,2) - исправен К-ый блок 1-го типа; В - исправен j-ый блок 2-го типа (j=1,2,3); С- прибор исправен. Происходит С, если исправны оба блока 1-го типа и хотя бы один блок 2-го. Выразить С через А и В.

2. Имеется множество {l,2,..,20}. Из него извлечено два числа. Определить вероятность того, что а) оба числа четные; б) одно четное, другое - нечетное.

3. На отрезке длиной L наудачу выбраны две точки. Какова вероятность, что расстояние между ними меньше половины L?

4. В урне 1 белый и 2 черных шара. Два игрока поочередно извлекают шары. Выигрывает тот, кто первый вынет белый шар. Определить вероятность выигрыша начинающего игру.

5. В тире имеется 5 ружей, вероятности попаданий из которых равны соответственно 0,5; 0,6; 0,7; 0,8; 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу.

6. Две кости одновременно бросают три раза. Определить вероятность того, что "двойная шестерка" выпадет точно один раз.

7. Случайная величина Х- выпадение "двойной шестерки" в предыдущей задаче. Найти: 1)ряд распределения,2)Функцию распределения и ее график, 3) M[X], 4)D[Х], 5)СКВО, 6) P{-1 }.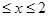

8. Дана плотность распределения

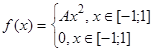
Найти А, F(x), M[X], D[Х], P{0<x }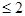

9. На заводе 1000 станков, каждый из которых выходит из строя в течение часа с вероятностью 0,001, Какова вероятность, что за смену (8 часов) выйдет из строя ровно 10 станков?

10. Случайная ошибка взвешивания подчинена нормальному закону (0, 20). Найти вероятность того, что при 3-х независимых взвешиваниях ошибка хотя бы одного не превышала по абсолютной величине 10 г.

1. Из таблицы случайных чисел наудачу взято число. События: А - число четное, В - число оканчивается на ноль. Что означают события АВ, .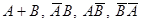

2. В конверте среди 25 карточек находится разыскиваемая карточка. Из конверта наудачу извлечены 6 карточек. Какова вероятность, что среди них нужная?

3. На отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит 0,1.

4. На полке расставлено 10 учебников, 4 из них в переплете. Взяли З учебника. Определить вероятность того, что хотя бы один из них будет в переплете.

5. Для контроля продукции из 3-х партий деталей взята для испытания одна деталь. Деталь с равной вероятностью может быть взята из каждой партии. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованных, а в 2-х других - все доброкачественные?

6. Вероятность попадания стрелка в яблочко при первом выстреле 0,25. Найти вероятность того, что будет не менее З-х попаданий при 5 независимых выстрелах.

7. Случайная величина Х задана рядом распределения

X	-1
P	а	0,3	0,4	0,1

Найти 1) а, 2)функцию распределения и ее график, 3)М[Х], 4)D[Х], 5)СКВО, 6)P{x 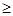1}

8. Функция распределения непрерывной случайной величины имеет вид

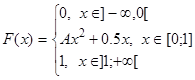
Найти A, M[X], D[Х], f(x), P{0 }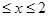

9. Устройство состоит из 500 элементов, каждый из которых выходит из строя в течение минуты с вероятностью 0,0002. Какова вероятность, что в течение часа выйдет из строя не более 2~х элементов?

10. Деталь считается высшего сорта, если отклонение ее длины от нормы не превосходит по абсолютной величине 0,45 мм. Случайное отклонение от нормы подчинено нормальному закону с параметрами (0,3). Определить среднее число деталей высшего сорта, если изготовлено 2 детали. Измерения длин деталей независимы.

1. Рабочий берет две детали. События: А-хотя бы одна из них бракованная, В - обе бракованные. Что означают события ?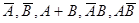

2. В записанном телефонном номере две последние цифры стерлись. Определить вероятность того, что это а) различные цифры, б) одинаковые цифры.

3. Значения а, b равновозможны в квадрате |a| 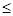1, |b| 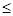1. Найти вероятность того, что корни квадратного трехчлена x²+2ax+b² положительны.

Дата добавления: 2014-12-16