Интервальные оценки параметров линейной регрессии

Поскольку статистика, используемая для оценки того или иного параметра, является случайной величиной, она может принимать произвольные значения, сколько угодно далекие от истинного значения оцениваемого параметра. Состоятельность статистики гарантирует лишь, что большие уклонения реализации этой случайной величины от оцениваемого параметра имеют малую вероятность, исчезающую при неограниченном возрастании объема выборки. При этом вероятность того, что истинное значение параметра в точности совпадет с наблюдаемым значением статистики, равна 0.

Интервальной оценкой параметра q генеральной совокупности с доверительной вероятностью g называется пара случайных величин, 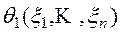и 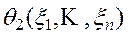, для которых имеет место неравенство 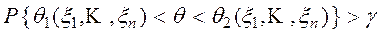при 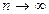. Если такие случайные величины найдены, то интервал

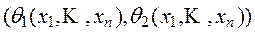
считается интервальной оценкой параметра q с доверительной вероятностью g. Подчеркнем, что в качестве достоверной оценки параметра q можно, как правило, указать только всю числовую прямую. Даже для значений параметра g,близких к единице (для этих значений доверительный интервал 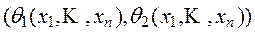обычно довольно велик, а прогноз относительно значения параметра q расплывчат), имеется возможность ошибки, то есть того, что на самом деле параметр q не принадлежит интервалу 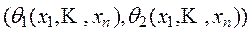. Вероятность этой ошибки равна 1- g.

Примером интервальной оценки математического ожидания генеральной совокупности в случае, когда среднее квадратичное уклонение известно и равно s, является доверительной интервал вида ,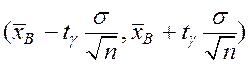

где t_g – решение уравнения 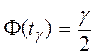. Здесь 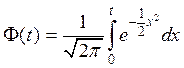– функция Лапласа.

Рассмотрим общую ситуацию. Предположим, что известно распределение некоторой состоятельной несмещенной статистики 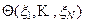параметра q генеральной совокупности. Если p (x) – плотность этого распределения, то вероятность уклонения статистики 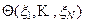от его математического ожидания q можно найти по формуле

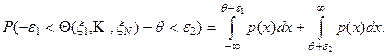
Рассмотрим, для простоты, распределения, симметричные относительно математического ожидания. Интервальную оценку параметра q также будем искать симметричной относительно значения 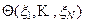. Величина t_g, удовлетворяющая соотношению

,

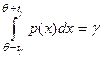является функцией параметра g и называется критической точкой распределения. В частности, для распределений, симметричных относительно математического ожидания, вероятность события

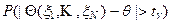
будет заведомо не больше 1- g. Интервал

называется доверительным интервалом параметраq с доверительной вероятностью g. В данном случае g есть вероятность события, что реализации случайных функци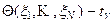й и 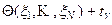удовлетворяют неравенству

.

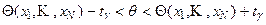Часто говорят, что g – это вероятность того, что интервал

“накроет” q.

Особую роль в построении интервальных оценок параметров линейной регрессии играет распределение c ² и распределение Стьюдента.

Пусть x ₁, …, x_n – n независимых нормально распределенных случайных величин с математическим ожиданием 0 средним квадратичным уклонением 1. Рассмотрим случайную величину

.

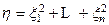Закон распределения этой случайной величины называется распределением c ² с n степенями свободы. В курсе теории вероятности доказывается, что функция плотности распределения этой случайной величины имеет вид

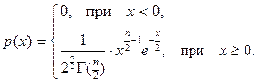
Среднее значение случайной величины, распределенной по закону c ², равно n, а дисперсия 2 n.

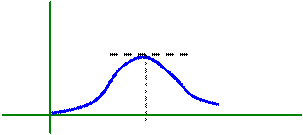p (x)

n -2 x

Замечательным фактом является следующее утверждение. Если n случайных величин x ₁, …, x_n удовлетворяют k независимым линейным соотношениям вида c ₀ + c ₁ x ₁ + … + c_nx_n = 0 (и, следовательно, среди них имеется n - k независимых случайных величин, а остальные линейно выражаются через них), то случайная величина 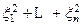, по–прежнему, имеет распределение c ², но уже с n - k степенями свободы.

Критической точкой распределения c² с числом степеней свободы n с уровнем значимости a называют решение уравнения

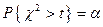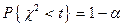Û Û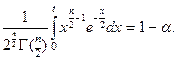

Решение этого интегрального уравнения обозначается 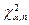и приводится во всех статистических таблицах. Приведем для справки команды, с помощью которых можно получить значения 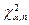при разных значениях параметров a, n в таких программах, как EXCEL, MATHCAD и MAPLE.

> with(stats):statevalf[icdf,chisquare[n]](1-a); (Maple)

qchisq(1-a,n)(MathCad)

=хи2обр(a;n) (Excel)

В частности, .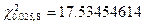

Пусть x ₀, x ₁, …, x_n – независимые нормально распределенные случайные величины с нулевым математическим ожиданием и одинаковым средним квадратичным уклонением s. Рассмотрим случайную величину

.

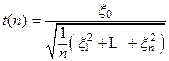Распределение этой случайной величины называется распределением Стьюдента с n степенями свободы. Функция плотности распределения этой случайной величины имеет вид

.

Среднее значение случайной величины, распределенной по закону Стьюдента с n степенями свободы равно 0, а дисперсия .

Нетрудно проверить, что при n ®¥ функция плотности распределения случайной величины t (n) стремится к функции плотности нормального закона N(0,1). Считается, что уже при n > 30 функция плотности практически неотличима от функции .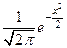

Если n случайных величин x ₁, …, x_n удовлетворяют k независимым линейным соотношениям вида a ₀ + a ₁ x ₁ + … + a_nx_n = 0, то случайная величина t (n) имеет распределение Стьюдента с n - k степенями свободы.

Критической точкой (двустороннего) распределения Cтьюдента с числом степеней свободы n с доверительной вероятностью g называют решение уравнения

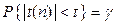Û

Решение этого интегрального уравнения обозначается 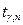и приводится во всех статистических таблицах. Приводим для справки команды, с помощью которых можно получить значения 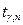при разных значениях параметров g и n с использованием программ EXCEL, MATHCAD и MAPLE.

> with(stats):statevalf[icdf,studentst[n]](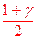); (Maple)

qt(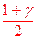,n)(MathCad)

=стьюдраспобр(1- g;n) (Excel)

В частности, .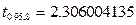

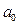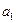Наша задача – предъявить интервальные оценки для параметров и линейной регрессии, а также оценку среднего квадратичного уклонения s случайной величины e в предположениях классической нормальной модели. Для этого требуется изучить закон распределения статистик

, , .

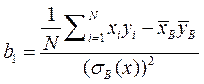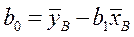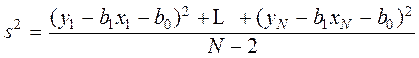Рассмотрим подробно распределение старшего коэффициента b ₁. В лекции 1 было получено соотношение

.

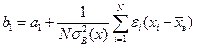Здесь 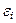– независимые, одинаково распределенные случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием и постоянным средним квадратичным уклонением s (нам неизвестным). При этом M[ b ₁]= a ₁,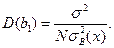

Из курса теории вероятностей известно, что произвольная линейная комбинация независимых нормально распределенных случайных величин распределена нормально. Следовательно, в предположениях классической линейной регрессионной модели, статистика b ₁ распределена нормально с параметрами a ₁, 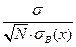. Отсюда сразу следует, что статистика 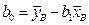также распределена по нормальному закону с параметрами

,

.

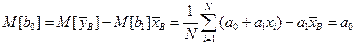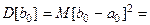
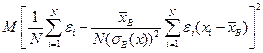
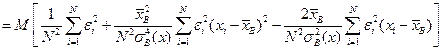
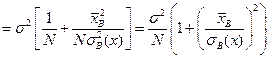К сожалению, параметр s нам неизвестен, и мы лишь можем оценить его при помощи статистики s ².

Определим закон распределения статистики s ². По определению остаточной суммы квадратов, имеем

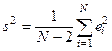, где .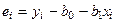

Из явного вида функций , , 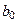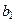следует, что случайные величины 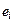выражаются в виде линейных комбинаций независимых нормально распределенных случайных величин 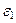, …, , 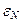следовательно, все 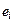также являются нормально распределенными случайными величинами. В лекции 1 были выведены формулы M [ e_i ]=0 и D [ e_i ]= 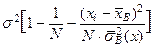. При достаточно больших значениях N можно считать, что все D [ e_i ] одинаковы и равны s ². Следовательно, с точностью до постоянного множителя, случайная величина s ² распределена по закону c². Вопрос лишь в том, какое количество независимых линейных соотношений имеется между величинами e ₁, …, e_N, или, иными словами, сколько степеней свободы имеет величина s ²? Вспомним, что для вывода формул для статистик b ₀ и b ₁ мы использовали принцип наименьших квадратов Гаусса, и, конкретно, два уравнения,

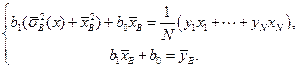
Таким образом, функции e ₁, …, e_N удовлетворяют двум независимым линейным уравнениям. Следовательно, число степеней свободы статистики s ²равно N -2:

.

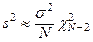С учетом соотношений 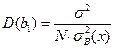, , 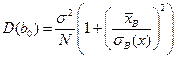отсюда следует, что случайные величины

,

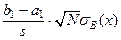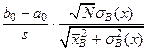
асимптотически, при N ®¥, распределены по закону Стьюдента с числом степеней свободы, равным N - 2.

Формулы для интервальных оценок параметров b ₁, b ₀. Если доверительная вероятность интервала равна g, то

,

.

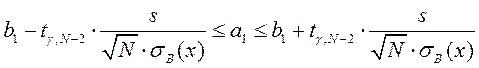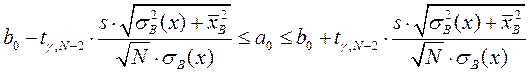Для доверительного интервала параметра s случайной величины e получаем выражение .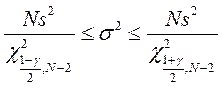

Действительно, поскольку 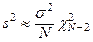, вероятность события 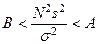(для положительных чисел A и B) равна

,

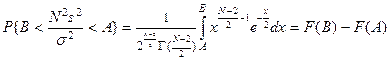где F (t) – интегральная функция распределения случайной величины c² с N -2 степенями свободы. В частности, по определению критической точки распределения c², получаем

.

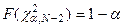Следовательно,

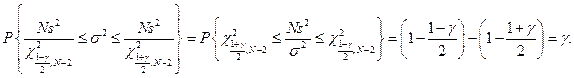
Таким образом, интервал 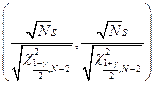“накроет” значение s с вероятностью g, что и требовалось.

Дата добавления: 2014-12-16