Коэффициента детерминации

Проверка гипотезы о значимости коэффициентов линейной регрессии. Оценивание качества приближения с помощью

Выше мы оценивали параметры линейной регрессии в условиях классической нормальной модели. Статистики, используемые для оценивания коэффициентов линейной регрессии, зависят от стохастической части регрессионной зависимости e. Даже если истинные значения параметров a ₁ и a ₀ равны нулю, реализации случайных величин b ₁ и b ₀, как правило, будут отличаться от нуля. Если параметры a ₁ и a ₀ равны нулю, мы будем называть их незначимыми. Наша задача – сформировать процедуру проверки гипотезы о незначимости коэффициентов линейной регрессии и уравнения регрессии в целом по найденным точечным оценкам параметров b ₁ и b ₀.

Статистическая гипотеза – высказывание о свойствах генеральной совокупности. Например, статистической гипотезой является предположение о том, что коэффициент a ₁ в уравнении регрессии равен нулю.

Ошибка 1 –го рода – это отказ от гипотезы в случае, когда она верна. Ошибка 2 –го рода – принятие гипотезы в случае, когда она не верна. Вероятность сделать ошибку 1–го рода при проверке гипотезы с помощью некоторого критерия называется уровнем значимости критерия. Вероятность не сделать ошибку 2–го рода называется мощностью критерия.

Любой возможный критерий проверки гипотезы о значимости коэффициентов регрессии основан на свойствах распределения случайных величин b ₁, b ₀ и s ². Напомним, что случайные величины

,

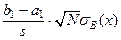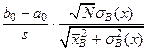
распределены по закону Стьюдента с числом степеней свободы, равным N - 2. В частности, если a ₁ = 0, то вероятность события

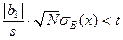
равна

.

Напомним, что критической точкой 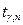распределения Стьюдента с числом степеней свободы n и доверительной вероятностью g называется решение уравнения

Следовательно, если гипотеза о равенстве нулю коэффициента a ₁ верна, то вероятность уклонения величины от нуля на величину не превосходит a = 1- g. Это дает следующий простой критерий проверки гипотезы о незначимости коэффициента a ₁ на уровне значимости a. Если , то гипотеза о равенстве нулю коэффициента a ₁ принимается. Иначе, гипотеза отвергается, и коэффициент a ₁ считается существенно отличным от нуля. Действительно, ошибку первого рода мы сделаем лишь в том случае, когда отвергнем гипотезу, то есть при условии .Но вероятность этого события заведомо не превосходит величины . Следовательно, уровень значимости критерия равен a.

Аналогично формулируется критерий проверки гипотезы о значимости коэффициента a ₀. Если

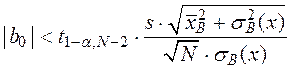
то гипотеза о равенстве нулю коэффициента a ₀ принимается. Иначе, гипотеза отвергается, и коэффициент a ₀ считается существенно отличным от нуля.

Дата добавления: 2014-12-16